传统公理的一般化理解：期望效用理论

期望效用由瑞士数学家伯努利于l738年首次提出，冯·诺伊曼和摩根斯坦等人（l944）在继承伯努利对“圣·彼得堡悖论”（St.Petersburg Paradox）解答的基础上，结合效用函数进行严格的公理化陈述而最终形成。冯·诺伊曼和摩根斯坦使用数学公理化方法提出他们的效用函数公理体系，最终使得该体系在逻辑上极具严密性。

在对期望效用函数进行公理化陈述之前，我们还需要了解一些基本概念。假设我们考虑的经济活动者是投资者，那么这一投资者会对自己的投资方案有其自己的偏好。他的投资活动可以用他投资的产品量来刻画，但是由于他现在面临的是不确定的投资环境，因此他面临选择的事件不再是确定的投资产品向量，而是投资产品的可能性组合。然后，投资者要对所有可能的组合作出优劣判断。在这里，假定我们从只涉及两个产品向量和一个概率的组出发来构造它们。假设L=（x，y，p），其中，x和y分别是两个产品向量，p∈[0，l]是概率，那么L=（x，y，p）表示投资者以概率p投资产品x，以概率（l-p）投资产品y。然后，我们再对两个这样的组L l=（x l，y l，p l）和L 2=（x 2，y 2，p 2）构造高层次的组L l=（L l，L 2，q），其含义类似。以此类推，对于这种高层次的组，我们还可以形成更高层次的组。最终我们实际上得到的是一个产品向量组，其中每一个产品向量都可以一定的概率被投资者所得到。由于所有的组在冯·诺伊曼和摩根斯坦的原著中并没有给出特殊的名称，我们将它称之为“未定产品”。这样，冯·诺伊曼-摩根斯坦公理的出发点就是“未定产品空间”□，它是由“确定产品空间”中的向量x，y等形成的L=｛（x，y，p）｝的组以及更高层次的组所组成的。但是需要指出的是，以x，y，z等表示□中的元素，它可能是“确定产品”，也可能是“未定产品”。同时在这个空间□中我们定义了一个偏好关系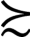。之所以在这里先做一些基本概念的说明，不仅是为了接下来更好地陈述期望效用理论的公理化体系，也是为了下文当中更清楚地介绍阿莱斯悖论。期望效用函数理论指出，只有满足自反性、传递性、完全性、连续性以及独立性公理假设的选择偏好，才可以被归结到期望效用最大化的原则范畴内。对于之前在第3章中我们重温远景理论时提到的相关公理，我们在此做更规范化的学术表达：

（l）自反性公理：对于任何x∈□，x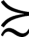x。即假设任何投资产品至少跟其本身一样好。

（2）传递性公理：对于任何x，y∈□，如果假设x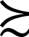y，并且y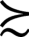z，那么就可以假定x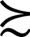z。即假设对于任意的x，y，z，如果x至少与y一样好，y至少与z一样好，那么就可以认为，x至少与z一样好。也就是说，如果投资产品x偏好于y，y又偏好于z，那么x一定偏好于z。

（3）完全性公理：对于任何x，y∈□，x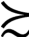y和y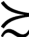x中至少有一个成立。即假设任意的x，y都是可以比较的，如果x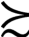y，或者y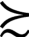x，或者这两种情况都存在，那么在这两种情况下，投资者对x，y是没有差异的。也就是说，对于两个投资产品，投资者总是会偏好于其中一个投资产品或者是同样偏好这两个投资产品。(www.xing528.com)

（4）连续性公理：对于任何x，y，z∈□，｛p∈[0，l]|（x，y，p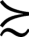）z｝和｛p∈[0，l]|z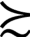（x，y，p）｝都是闭集。即关于任意的x 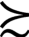y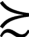z，对于任意的p∈（0，l），总存在唯一的p，使得px+（l-p）z=y。需要指出的是，当投资产品x偏好于y时，即使x中某几个状态对应的概率发生微小改变，x仍然偏好于y，也就是说原来的偏好顺序不发生改变。

上述四个公理假设都是非常贴近现实的假设，如果我们放弃这些公理假设，则会导致经济学很难在一定的数理框架下进行分析。

（5）独立性公理：对于任何x，y，z∈□，如果x～y，即x等价于y，那么对于任何p∈[0，l]，（x，z，p）～（y，z，p）。独立性公理也被称为替代性公理，这条独立性公理是说x与y的无差别不受其他可能性的影响。进一步地，如果决策者对投资产品x和y之间存在一个偏好关系，那么将投资产品z按相同的比例分别与x，y组合后，产生新的投资产品x′，y′保持与x，y相同的偏好关系。即如果x≻y，那么对于任意的p∈（0，l），都有px+（l-p）z≻py+（l-p）z。