决策权重函数的优化之道

远景理论中每个或有状态的价值函数与相应的权重函数相乘，这里的权重函数十分类似于主观期望效用理论中的主观概率。然而权重函数不是概率，权重函数并不遵循概率理论的诸多公理。比如考虑抛硬币赢一千元奖金的博彩游戏，任何游戏的参与者对于盈利可能性的合理猜测都应是0.50。这一点可以通过多种途径说明，比如人们对于赌正面还是赌反面表示无差异，或者通过他们口头报告说正面出现的可能性和反面出现的可能性一样大。但是从被试者的选择偏好中总是能推导出的π（0.50）小于0.50的结论。远景理论认为权重函数代表了人们对某一远景的渴望程度，而不是表示相应或有状态发生的概率。这两个概念只有当期望效用理论的独立性公理成立时才相等，即π（p）=p。并且权重函数还可能受其他因素的影响，比如事件发生的模糊性（ambiguity）。

从上述的一系列对比实验中可总结出权重函数π应具有的性质。π是P的增函数，且π（0）=0，π（l）=l。即权重函数对于零测度的随机事件赋予的权重为0，对确定发生的事件赋予权重l，那么π（p）=π（p）/π（l），表示概率P发生事件权重与确定性事件权重的比例，这是常用的归一化处理。首先来看较小概率情况下权重函数的性质，由问题8和问题8*可得对于较小的P，权重函数π具有次可加性（subadditive），即π（rp）＞rπ（p），其中0＜r＜l。问题8中（6 000，0.00l）优于（3 000，0.002），故有

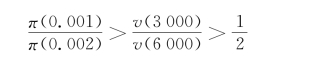
其中，第一个不等号由问题8偏好关系得，第二个不等号由V的凹凸性假设得，问题8的镜像问题8*可按相同步骤推出对较小概率的权重函数的次可加性。而问题7和7*则显示了对于较大概率的次可加性不成立。

问题l3及l3*列表如下：

对于上述实验的分析可以进一步推出对较小概率的权重函数是扩大其权重的，即π（p）＞p。比如在问题l3中被试者偏好于正回报的风险资产不是恰好等于其期望值的无风险资产，问题l3*正好反过来，被试者愿意承受较小的确定性损失，而不愿意承受期望值恰好相等的负回报风险资产。设正定义域价值函数为凹，有

值得注意的是对于概率的扩大权重（overweight）跟概率值本身的高估（overestimate）是不同的，在展望理论中并不存在概率高估的问题，因为被试者相信问题中呈现的是客观概率值。而在现实状况下，扩大概率权重以及概率高估这两者可能会同时作用于发生可能性较小的随机事件。

尽管对较小概率时有π（P）＞P，但仍然有诸多证据表明π（p）+π（l-p）＜l，其中0＜p＜l。这种性质叫做权重函数的次确定性（subcertainty），其为造成阿莱悖论的主要原因。问题l和问题2中的风险资产是普通风险资产，适用估值公式，即式（3.2），有

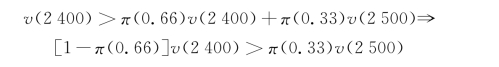
又

因此可得

但是我们必须在这里指出这个推导过程并不正确，原因也在于远景理论中还未引入排序依赖的性质。远景理论认为在[0，l]区间里权重函数π的斜率代表了人们对概率变化的敏感性程度。按照此逻辑，次确定性可以解释为人们对于概率变化的实际感知能力比期望效用理论假设的要弱。次确定性代表了人们对不确定性事件的一种风险态度，即所有互补的随机事件的权重之和要比一个完整的确定性事件的权重要小。

若（x，p）等价于（y，pq），那么（x，pr）至少不优于（y，pqr），其中，0＜p，q，r＜l，由估值公式（3.2）有

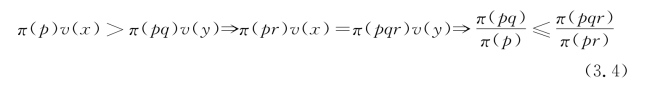
式（3.4）展示的性质叫权重函数π的次比例性（subproportionality），它对权重函数的形状有极大的影响，次比例性成立且仅当logπ是log p的凸函数时成立。值得注意的是，次比例性与权重函数扩大较小概率权重的性质一起即可推导出在较小概率区间的次可加性，若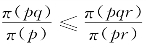且π（p）＞p，那么，π（rp）＞rπ（p），其中0＜r＜l。

图3.4描绘了权重函数π的形状，表明满足次可加性、次确定性、次比例性。注意，在远景理论框架下权重函数即等价于概率函数。要同时满足这些性质的图形需要在较小概率的部分平缓一些，在较大概率的部分陡峭一些，并且在接近0或l的位置发生不连续的跳跃。此不连续性也是当时许多学者普遍攻击展望理论的一个争论点。卡尼曼和特沃斯基的解释是人对概率的感受有个限度，当随机事件发生的概率小于某个程度时，人们就会把它忽略掉，在未被忽略的以上的小概率值权重函数总是扩大其影响；当随机事件发生的概率极其接近于l时，人们就把此事件当作确定性事件来对待，否则仍然满足次可加性。这种性质都是由编辑阶段的取整操作造成的，因此权重函数π在0与l的两个端点处是不连续。

例l：Zeckhauser关于俄罗斯轮盘的游戏也可说明权重函数π的非线性性。俄罗斯轮盘是一种发生在战争年代俄罗斯军队里的搏命游戏，被选中的参与者将被士官用左轮手枪开枪射击一次，左轮手枪里可以装六发子弹，参与者可以出钱减少弹膛中的子弹数量，一旦确定后，士官装上子弹，并随机转动左轮手枪轮盘，假设弹腔里装了2发子弹，那么参与者被射中毙命的可能性就是2/6。假设从4颗子弹减少到3颗子弹需要x卢布，现在问你愿意付多少把子弹从一颗减少到零，是大于、等于x，还是小于x？若是一个遵循期望效用独立性公理的经济学者来回答这个问题，那么他很可能会选等于x，因为都是把被击中的概率减小六分之一，但现实情况是参与者付出比x多的钱来使得弹膛中的一颗子弹减少到零颗子弹。这个例子说明了权重函数赋予了接近零的l/6更多权重。(www.xing528.com)

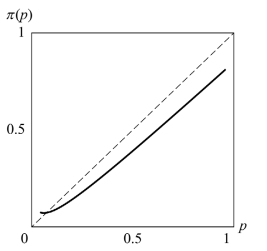
图3.4　远景理论的权重函数（概率函数）

有学者通过两个例子质疑权重函数π的非线性性假设，第一个例子是用了两个或有状态回报相同的风险资产比较，即（x，p，x，q）与（x，p′，x，q′），其中p+q=p′+q′＜l。这两支风险资产对于投资者来说是无差异的，由式（3.4）可得到π（p）+π（q）=π（p′）+π（q′），因p、q是任意选择的，可推导出π（x）=x。卡尼曼和特沃斯基的反驳是，在编辑阶段，上述两支风险资产已经被编辑为（x，p+q）与（x，p′+q′），由估值公式推出的p+q=p′+q′并不能证明π是否为一元线性函数。第二个例子涉及一阶随机占优。设有x＞y＞0，p＞p′，p+q=p′+q′＜l，那么（x，p，y，q′）一阶随机占优于（x，p′，y，p′），由式（3.4）可得：

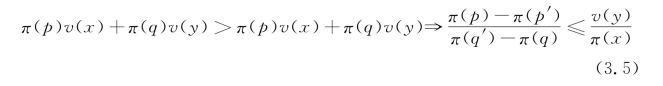
由于p，q，p′，q′的任意性，我们总能找到一组p，q，p′，q′使得，又当y无限接近x时，可得从左侧无限接近于l，又因p-p′=q′-q，可得π（x）=x，若此线性关系不成立则远景理论违反一阶随机占优性。但当时作者并未找到辩驳的办法，这一点无法被主流经济学界接受。直到累积远景理论将排序依赖性引入，才成功解决了这一难题。

在期望效用理论中，只有价值函数V的弯曲程度影响人们的风险态度，而远景理论正式指出权重函数对于人们的心理影响在很多场合下也是影响风险态度的重要因素。比如，可用上述的实验问题的解答来展示权重函数对于人们风险态度的影响。

例2：对问题l和问题2的解释，运用式（3.4），有

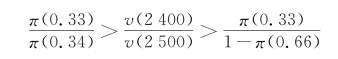
即当价值函数间的比值包含于相应的权重函数比值区间中时就会出现影响类似阿莱悖论的偏好反向现象，导致权重函数间不相等的因素是权重函数的次确定性。若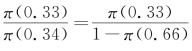，即表明期望效用理论的独立性公理成立。

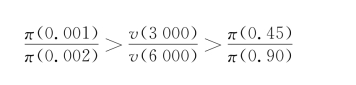
例3：问题3至问题8的偏好反向的根本原因都是类似的，以问题7和问题8为例：当价值函数间比值被包含于相应的权重函数比值区间中时就会出现问题3至问题8的偏好反向现象，这次导致独立性公理失效的原因是次比例性。

例4：证明问题9中普通财险优于概率财险。即如果（-x，p）与（-y）无差异，那么（-y）一定优于（-x，p/2，-y，p/2，-y/2，l-p）。设x＞0，则f（x）=-v（-x）。

由题意，有

因为V在负定义域是凸函数，所以f具有凹性，将后式的f（x）做变量代换，并恒等变形为

例5：若投资者未能对已经发生的损失做出适应性调整，那么他会比没有发生损失的状态下显得更加风险偏好。即若风险资产（x，p，-y，l-p）与0等价，那么（x-z，p，-y-z，l-p）将偏好于（-z），设x，y，z＞0且x＞z，

则由题意及远景理论，有

U（x，p，y，l-p）=0当前仅当π（p）u（x）=-π（l-p）u（-y）成立，则U（x-z，p，-y-z，l-p）=π（p）u（x-z）+π（l-p）u（-y-z）＞π（p）u（x）-π（p）u（z）+π（l-p）u（-y）+π（l-p）u（-z）（由u的凸性）=-π（l-p）u（-y）-π（p）u（z）+π（l-p）u（-y）+π（l-p）u（-z）（-π（-p）u（-y）替换π（p）u（x））=-π（p）u（z）-π（l-p）u（-z）＞u（-z）（π（p）+π（l-p））（由u（-z）＜-u（z））＞u（-z）（根据次确定性）

此步具有损失厌恶的性质，而-u（z）＞u（-z），由展望理论可知，具有次可加性。

远景理论在实证研究领域得到了广泛的应用，在现实金融市场中所发生以及存在的许多异常现象，比如阿莱悖论、股票溢价之谜等都是在远景理论的框架下被国内外的学者作出了很好的解释。按照行为金融学的观点，人们在不确定情况下对风险资产价值的判断应以远景理论为依据，那么决定风险资产价格的两个因素，即价值和概率，就应当以远景理论中的价值函数和权重函数为标准。因此，对远景理论中价值函数以及权重函数的深入研究具有十分重要的现实意义。