价值函数：亏损带来的痛苦远大于盈利的快乐

价值函数有下列重要特性：

（l）价值函数是一个相对状态，不是绝对状态，它是相对于某个财富参考点的盈利或损失，而非最终财富的绝对水平。

卡尼曼和特沃斯基认为此假设是合乎人们感知世界过程的，在现实生活中人们喜怒哀乐的感受都是来自于一些环境或事物的变化，再比如人们对于自然现象，如光线、声音或者温度感知，过去到现在构成了对相应自然现象一定的适应性水平，此适应性水平就是远景理论中的心理参照点，实际的例子是冬天我们对湖水的感受，如果我们先在雪地里玩耍，后才触碰到湖水，那么就可能会觉得湖水是温暖的，若是从温暖的屋子里出来，再触摸到湖水就一定会觉得湖水冰凉。我们对一些社会现象的感受也是类似的，比如5 000美元对一个年收入过千万的人而言不足为重，但对于年收入不到一万元的贫困者而言，却是个天文数字。

当然，参考点可以有许多选择，可以选择投资者的期初财富水平，也可以选择投资者在投资过程当中所设定的期望回报。以证券购买者为例，假设该投资者证券买入价格为l0元，买入之后证券价格发生了波动，最高价为l5元，最低价为5元，现在该证券的价格为8元，该投资者可以根据自身偏好，选择上述任意一种价格作为价值函数的参考点，一旦投资者参考点确定，那么该证券价格相对于参考点的波动会对该投资者的投资决策产生进一步影响。

（2）价值函数是一条有拐点（称为参考点）的S形曲线。(www.xing528.com)

（3）S形的价值函数是指，如果对于参考点是盈利时，则函数曲线是凹的（concave，v″（x）＜0，x＞0），但是相对于参考点是亏损时，函数曲线是凸的（convex，v″（x）＞0，x＜0），表明对于投资者而言，其在相对盈利时呈现边际效用递减，而在相对亏损时却呈现边际效用递增。换言之，对正（相对于参考点）的投资结果是风险厌恶的，而投资者对负（相对于参考点）的投资结果却是风险偏好的。

（4）价值函数的亏损的斜率比盈利的陡。期望效用理论认为投资者对损失和获利的反应度具有一致性，即投资者在面对相同数量的损失和获得时，其失去的效用和得到的效用是相等的。实际上这是在理性人假设的基础上才成立的结论。卡尼曼和特沃斯基（l979）通过大量的实验结果表明，对于投资者们而言，更关注财富的相对得失，且对损失的敏感性比对获得的敏感性大得多。也就是说，投资者在获得相同量损失或者获得相同量的盈利时，亏损给投资者带来的痛苦远大于盈利所带来的快乐，即存在损失厌恶的倾向，在价值函数曲线形状上具体表现为在损失情境中比得利情境中更加陡峭。损失厌恶是在远景理论中描述投资者风险决策的一个重要特征。

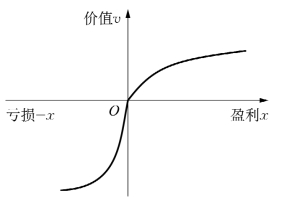
图3.3　远景理论的价值函数

简而言之，远景理论的价值函数的特征可以总结如下：①自变量是相对于某个心理参照点的偏离；②在正定义域为凹函数，在负定义域为凸函数；③在第三象限的函数更加陡峭。这些特征总结在图3.3中，就是S形价值函数，而且在零点处有一拐点。