流参量转换模式的优化探究

效应知识有多种表达方式。从系统论的角度，用输入、输出之间的变化关系进行描述是常用的一种方法。输入量、输出量可以用流的方式进行定义，如图4-5所示。

图4-5 效应模型

例如，安培定律、平面凸轮机构均是广义效应的具体形式，其输入流和输出流之间的转换关系见表4-5。

表4-5 效应及其输入流、输出流

效应集合GE与功能基集合FB之间的映射关系建立在工程经验的基础上，如图4-4所示。

根据输入流与输出流的关系，广义效应模型定义如下：ge={＜input_flow＞，＜f＞，＜output_flow＞}，其中＜input_flow＞，＜output_flow＞分别为效应的输入流、输出流，＜f＞为输入流与输出流之间的函数关联。＜output_flow＞中的特定参量往往与特定目标功能的实现相关，其成为构建功能元映射过程的基础。

总结工程经验是在工程实践之后的智力活动，由于设计过程与约束条件的复杂性，所以可能导致特定的分功能（功能基）求解无法通过功能元映射过程实现，需要寻求另外的求解过程。

设x为与目标功能有关的流集合中的成员，且x∈＜input_flow＞，则可以通过转换＜f＞为＜f′＞，重新确定输入流与输出流，即＜input_flow′＞与＜output_flow′＞，满足x∈＜output_flow′＞，而不改变效应的本质过程，即ge={＜input_flow′＞，＜f′＞，＜output_flow′＞}，其中＜f′＞是实现效应ge与功能需求的作用方式。上述效应的应用过程称为流参量转换模式。(www.xing528.com)

以安培定律为例，如图4-6所示，使带电流的导线处于磁场中，导线将受到力的作用，计算公式为：N=IBlsinθ，其中I为电流，B为磁场强度，l为导线的长度，θ为磁场方向与电流方向的夹角，N为产生的机械力作用。安培定律可描述为：Amperes_law={＜I，B，l，θ＞，＜f＞，＜N＞}。

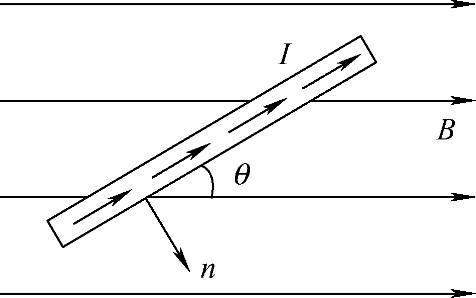
图4-6 安培定律

根据工程经验，通常将效应知识“安培定律”与分功能（功能基）“提供力”相互关联，建立映射关系。

如果设计过程中的分功能（功能基）为“测量磁场强度”，则磁场强度B为与功能需求相关的流参量。通过现有的映射关系（“安培定律”与“提供力”），不能检索出“安培定律”与“测量磁场强度”的相关关系，即两者可能不存在已有的映射关系。

通过流参量转换过程，安培定律可描述为：Amperes_law={＜I，N，l，θ＞，＜f′＞，＜B＞}。其中，＜f′＞的作用关系为

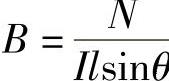
从而实现了“安培定律”效应与“测量磁场强度”目标功能之间的关联。

流参量转换过程是对功能元映射过程的补充与拓展，其丰富了功能推理的方式，有助于发现新的功能元映射关系。