变量选择及模型概览

在参考Armesto et al.（2010）以及Conrad et al.（2014）等文献的基础上，本书将宏观经济变量划分为两大类：第一类测定了当前经济形势，第二类则为前瞻性指标。第一类指标包括工业生产值（IP），非农就业（NFP），中美利差，美国长短期国债利差，美国联邦基金期货隐含利率以及美国经济政策不确定性指数（EPU）等，前瞻性指标则包括先行指数（LI）。先行指数由费城联储发布，基于经济领先变量如住房许可，失业，保险索赔，ISM制造业配送时间以及期限利差预测美国未来6个月coincident index的增长率。前瞻性指标可反映市场参与者对未来经济发展的预期。

经过多轮尝试和反复试验，本书选取Shibor-3M和美国3个月国债收益率之差作为中美利差的代理变量，美国10年和3个月国债收益率之差作为美国长短期国债利差的代表性变量，美国联邦基金期货隐含利率以及隐含利率变动率（一阶差分）作为市场对美联储货币政策的预期变量，美国3个月国债收益率以及3个月国债收益率日变动率（一阶差分）作为美国短期利率指标，美国经济政策不确定性（Economic Policy Uncertainty）指数EPU作为美国经济政策不确定指标，波动率指数日变动率（一阶差分）作为市场风险指标，美国经济先行指数“LI”代表美国国内宏观经济预期指标。此外，为尽数考虑不同政策和经济变量所包含的信息并研究他们的综合效果，我们使用主成分分析法从各变量中提取主要成分进行分析。该方法的优势在于可大大降低参数个数并提高模型的计算和估计效率。以上数据均为月度数据。为节省空间，此处不再给出以上各政策和经济变量的描述性统计分析结果。

在介绍GARCH-MIDAS模型前，我们先简要介绍Ghysels et al.（2004）提出的混频数据抽样模型（Mi（xed）Da（ta）S（ampling）approach，缩写为MIDAS模型），该模型可巧妙实现在同一模型中处理和估计不同频率数据的问题。MIDAS模型形式如下：

α为截距项，β为斜率，εt则被设定为零均值且方差为σ2的独立同分布序列εt～i.i.d.（0，σ2）。中的滞后项t-k/m为时间单位t-1和t之间的时间片段。更具体而言，若t代表的是月度数据的时间刻度，而美国某政策或经济变量为周度数据，则m=4。若联邦基金目标利率在月度t第二周公布，则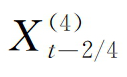代表联邦基金目标利率的宣布日期。若当月无其他政策或经济变量宣布，则我们将　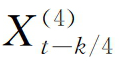，k=1，3或4设定为零。参数k代表美国政策或经济变量和月度t最末期之间的时间区间，而kmax则代表整个时间汇报期（如月度t）的相对频率更高的数据频率的时间刻度（在本例中为4）。当k＞kmax时，变量Xt对Yt的影响可忽略不计。权重Γ（k，θ）由k和n维超参数向量θ决定。Γ（k，θ）具有数种形式，如无限制MIDAS多项式（U-MIDAS），正规化beta概率密度函数，正规化指数Almon滞后项多项式，P阶Almon滞后项多项式，步函数等。

其中由Foroni，Marcellino and Schumacher（2015）提出的无限制MIDAS（U-MIDAS）多项式意为可在无限制的条件下对单个参数进行简单回归估计，且当m取值较小时，仍可进行有效估计。U-MIDAS是步函数的一种特殊情形。

正规化beta概率密度函数为：

wherexi=i/（N+1）

正规化指数Almon滞后项多项式为：

P阶Almon滞后项多项式（未正规化，单个权重之和不等于1）为：

这也可写为以下矩阵形式：(www.xing528.com)

步函数形式为：

通过将Engle and Lee（1999）提出的成分GARCH模型和Ghysels et al.（2004）提出的MIDAS框架相结合，GARCH-MIDAS模型可将条件方差分解为长期和短期成分，经平滑后的金融资产已实现波动率或低频数据通过长期成分对金融资产收益率的条件方差产生影响。GARCHMIDAS模型框架使我们可将日度金融资产数据和频率相对较低的宏观经济变量相连接，以研究宏观经济变量对金融市场波动的影响。

和Engle et al.（2013）的研究有所区别，本书主要聚焦于考察美国政策和经济变量对中国股指期货市场波动的预测能力，并检验相对于无外生变量的基准模型，加入外生经济变量是否可以提高GARCH-MIDAS模型的预测能力。

正式的GARCH-MIDAS模型如下所示：

Nt为月度t所包含的交易天数，Φi-1，t为截至月度t第i天的市场信息集。动态条件方差的短期成分gi，t服从（日度）GARCH（1，1）过程：

动态条件方差的长期成分τt等于经MIDAS回归后平滑的金融资产已实现波动率或外生经济变量：

Xt既可为外生经济变量，也可为已实现波动率。当Xt为已实现波动率时，RVt=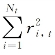。其中K为对已实现波动率或经济变量进行平滑的时期数。τt在固定时间区间内是恒定不变的（当使用滑动窗口分析法时，τt在每个时期内均变化）。

经过多次尝试，本研究权重函数使用以下Beta滞后多项式来表示：

需要注意的是，在本书的非线性设定中，只能根据θ正负推断宏观经济变量对长期波动成分的影响，不能根据其大小判断经济变量对长期波动成分影响的边际效应。本书设定ω1=1以保证权重函数呈衰减趋势。ω2＞1且ω2的大小可用来判定权重函数衰减的速度，ω2越大，权重函数衰减的越快。一般而言，φk（ωi）非负且总和为一。