数据选取与模型构建的优化方案

（一）变量选择

对于美国货币政策而言，美联储可直接影响的变量为联邦基金利率，作为隔夜拆借利率的一种，联邦基金利率反映了银行间资金的余缺和银行间短期资金拆借的成本，是美国短期利率的代表。美国3个月国债收益率与有效联邦基金利率（effective federal funds rate）走势十分接近，常被用来作为货币政策的代理变量（Yang and Hamori，2014；Asgharian et al.，2015）。由利率期限结构理论可知，市场中长期利率在很大程度上取决于市场对于基准利率未来走向的预期，更进一步而言，取决于市场对于未来货币政策走向的预期，当下的货币政策（基准利率水平）则对其影响很小。因此，美国10年期国债和3个月国债收益率之差一方面反映了市场对美国未来货币政策走向以及美国国内宏观经济走势的预期；另一方面也间接与美国消费者对中国出口商品的需求以及美元汇率相关联，并进一步影响中国国内长期固定资产投资、企业资金需求、股市和债市的走势。因此，在参考Bernanke and Blinder（1992）的基础上，本书选取美国10年期国债和3个月国债日收益率之差TBspreadt作为美联储货币政策代理变量之一。

与此同时，中美利差对国际资本在两国间的流动有着巨大的影响，中美利差的变动必然会影响到中国资产价格、利率水平以及股市的波动。由利率平价理论可知，中美利差对人民币汇率变动有着不可忽视的影响，而汇率的变动又会进一步影响国际资本流向、国内资产价格、对外贸易、国际收支乃至国内的宏观经济运行状况。因此，本书同时使用中美利差USCNspreadt作为中美货币政策代理变量，研究中美利差与中国金融期货收益率间的交叉相关关系。

前文已有所提及，美国3个月国债收益率作为美国短期利率的代表性变量，被诸多文献采用为联邦基金利率的替代变量（如Sun et al.，2017），同样的，本书使用美国3个月国债收益率作为美国联邦基金利率和短期利率的替代变量。上海银行间同业拆放利率（Shibor）是由具有较高信用等级的银行所报同业拆出利率的算术平均值，在一定程度上反映了市场对利率走势的预期，是相对市场化的利率。已有研究表明，Shibor和国内银行间拆借利率、回购利率等有关利率间存在较强的关联性，其基准利率属性随着利率市场化的推进而逐步增强（方意和方明，2012），因此，本书采用同样为3个月期限的Shibor-3M作为中国市场化短期利率的代表。将Shibor-3M和美国3个月国债收益率之差作为中美利差USCNspreadt的代理变量。从另一个角度而言，美国短期国债是被认为最安全，完全零违约风险的证券，而Shibor利率报价行都是信用等级较高的大银行，违约风险很低，两者之差有些类似于TED利差（泰德价差），一定程度上反映了中美两国金融市场的风险状况。在美国，当风险较高时，投资者会出售资产并购买相对安全的美国短期国债，从而拉低美国短期国债收益率。在中国，当风险加强或市场流动性告急时，银行间拆借利率会迅速走高，Shibor利率会上升。在该情况下，中美利差USCNspreadt会被拉大。因此，该利差的上升意味着市场间风险的加剧和借贷意向的走低，选择该变量也就从风险测度和市场情绪的角度对影响股指期货和国债期货的又一因素进行考察。

（二）数据选取和初步统计分析

考虑数据的可得性和代表性，本研究选取了2010年4月16日—2016年10月31日间沪深300股指期货，2013年9月6日—2016年10月31日间5年期国债期货作为中国金融期货市场的代表性金融期货品种，两种期货皆选取连续合约每日收盘价作为研究对象，数据均来源于Wind金融数据库。图6-1展示了沪深300股指期货、5年期国债期货连续合约每日收盘价、每日收益率以及中美利差和美国长短期国债利差走势图。表6-1展示了各期货每日收益率、两种货币政策代理变量每日数据的描述性统计结果，其中期货每日收益率采用ri，t=log（Pi，t）-log（Pi，t-1）计算，Pi，t和Pi，t-1分别为第t日和第t-1日对应期货i的收盘价。

图6-1显示，无论是沪深300股指期货和5年期国债期货每日收盘价序列，还是中美利差和美国长短期国债利差，其波动均较为剧烈。在美联储退出量化宽松货币政策至开启新一轮加息周期的时间段内，沪深300股指期货日收盘价波幅明显大于其余时间段的波幅，而5年期国债期货日收盘价在2014年以后呈现出波动中逐步上升的趋势。中美利差和美国长短期国债利差走势大体一致，但不同利差间存在一定的差值，两利差在美联储退出量化宽松货币政策后波动幅度明显加大，但利差本身自QE4结束后呈现逐步下行的态势。从两期货日收益率图的纵坐标刻度可以看出，沪深300股指期货和5年期国债期货日收益率波动幅度均不太大，其中沪深300股指期货日收益率在2015年下半年波幅加大，而5年期国债期货日收益率的波动幅度在2015年也有所增大。

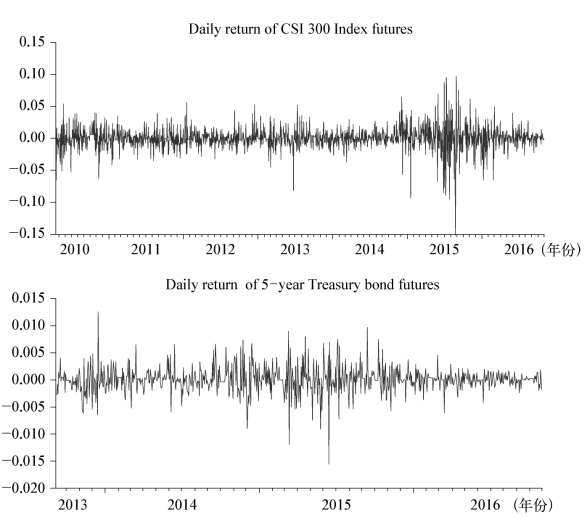
图6-1　金融资产价格及收益率时间序列

注：第一和第二行分别为沪深300股指期货、5年期国债期货每日收盘价和中美利差、美国长短期国债利差的时间序列走势图。“FFR Hike”代表2015年12月美联储的加息时点；第三、四行为沪深300股指期货和5年期国债期货每日收益率图示。

由表6-1可知，沪深300股指期货和5年期国债期货日收益率均值皆接近于0，偏度均不为0，峰度都远远大于3，且JB检验结果也证实两序列都不服从正态分布，ADF检验结果表明两时间序列均在1%显著性水平下拒绝含有单位根的原假设，即两序列均为平稳序列。对于中美利差和美国10年期和3个月国债日收益率利差而言，两序列偏度均不为0，但峰度均小于3，不服从正态分布且序列不平稳。总体而言，沪深300股指期货和5年期国债期货日收益率序列均呈现出有偏、尖峰、厚尾的非正态分布特征。

表6-1　样本数据描述性统计结果

注：沪深300股指期货和5年期国债期货均为日收益率数据，“JB检验”代表Jarque-Bera检验，用于测定时间序列的分布特征，原假设为该时间序列遵循正态分布。“ADF检验”代表ADF单位根检验，用于测定时间序列的平稳性，原假设为时间序列含有单位根。***，**，*分别表示在1 %，5%，10%的显著性水平下显著。

为初步定性的检验中国金融期货和中美利差以及美国10年期和3个月国债日收益率利差间是否存在交叉相关关系，我们采用Podobnik et al.（2009）所提出的交叉相关检验法进行检验。该检验和Ljung-Box检验有一定的类似性（Ljung and Box，1978）。Ma et al.（2013）使用该方法检验了WTI原油和BRIC股市间的交叉相关关系，Pal et al.（2014）同样使用该检验分析了原油、黄金和汇率间的交叉相关关系。

具有相等时间长度的两序列x（i）和y（i）的交叉相关检验量Qcc（m）如式（6.1）所示。

交叉相关方程如式（5.2）所示。

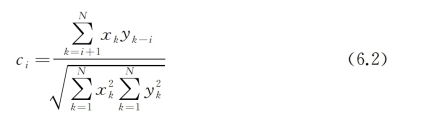
统计量Qcc（m）服从自由度为m的Χ2（m）卡方分布。若交叉相关统计量Qcc（m）大于Χ2（m）分布的临界值，则前m个交叉相关系数等于零的原假设被拒绝，也即两序列间存在交叉相关关系。图6-2绘制了各对时间序列间的交叉相关统计量，在5%显著性水平上的Qcc（m）统计量的临界值如图中直线所示。因样本数据量所限，对股指期货和两大利差，其统计量的自由度m取0到1 000，对国债期货和两大利差，其统计量的自由度m取0到800。

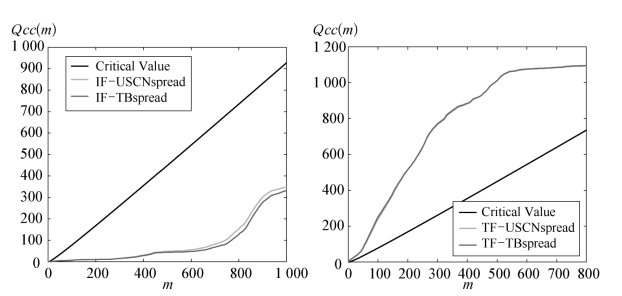
图6-2　交叉相关性检验统计量Qcc（m）

由图中可清晰地看到，对于股指期货日收益率和美国货币政策代理变量，其交叉相关系数Qcc（m）低于临界值，而对于国债期货日收益率和美国货币政策代理变量，其交叉相关系数Qcc（m）高于临界值，意味着第二对时间序列间有着统计上显著的交叉相关关系。

为进一步考察每对变量间的交叉相关关系，本研究接下来进一步计算ρDCCA系数（Zebende，2011）。该系数为去趋势协方差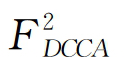与两个去趋势方差FDFA乘积的比值（关于FDCCA和FDFA的计算方法，下文将有阐述）。Sun et al.（2017）采用此系数检验了美国货币政策，美元指数和WTI原油价格间的交叉相关系。

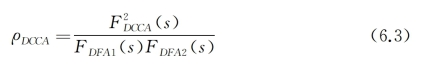
ρDCCA的取值范围为-1至1。当ρDCCA=0时，两序列间不存在交叉相关关系。当ρDCCA=-1时，两序列间的交叉相关关系是完全反持续的。ρDCCA=1则表明两序列间的交叉相关关系是完全持续的。表6-2汇报了不同时间窗口长度s（s=8，16，32，64，128，256）下ρDCCA的取值。

表6-2　不同时间窗口s对应的ρDCCA系数

注：括号内为P值。(www.xing528.com)

对于每对时间序列，均存在在10%显著性水平下显著的ρDCCA系数。显著的ρDCCA系数之取值均落于（-1，1）区间内，且没有零值，表明各对时间序列间存在交叉相关关系。

（三）模型构建

为进一步量化序列间的交叉相关关系，以下将简要阐明多重分型去趋势交叉相关分析（MF-DCCA）算法的步骤。假设存在两个时间序列x（i）和y（i）（i=1，2，…，N），N是时间序列的长度。

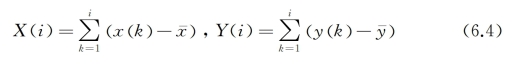
第一步，构建两个时间序列均值离差的累积和。

和分别代表两时间序列x（i）和y（i）的均值。

第二步，将两时间序列X（i）和Y（i）各自均值离差的累积和序列切分成Ns=int［N/s］块互不重叠的部分或时间窗口。鉴于N并不一定是时间块s的整数倍，为将未包含在时间窗口中的序列末端数值也加以考虑以保证信息的完整性，我们将序列X（i）和Y（i）从末端到首端重新进行一次切分。这样我们就得到了2Ns个互不重叠的时间窗口。

第三步，为得到每个时间窗口ξ中两序列的去趋势协方差，我们在每个时间窗口中采用m阶多项式构建两序列各自的局部趋势。

对于ξ=1，2，…，Ns，每个时间窗口ξ中两序列的去趋势协方差可表示为如下形式：

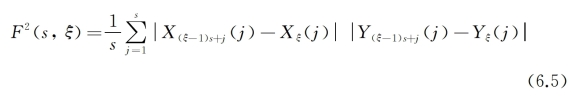
对于ξ=Ns+1，Ns+2，…，2Ns，每个时间窗口ξ中两序列的去趋势协方差可表示为：

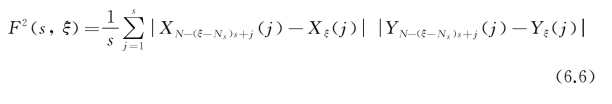
Xξ（j）和Yξ（j）分别代表在每个时间窗口ξ中所拟合的X（i）和Y（i）的m阶多项式。

第四步，将所有时间窗口ξ中的去趋势协方差经如下处理，我们可得到如下q阶波动方程：

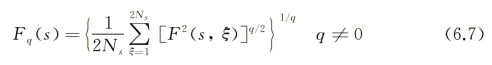
q=2时，MF-DCCA退化为DCCA。q在一定程度上反映了波动的大小，q＜0时为小型波动，q＞0时代表大型波动。

第五步，标度指数（scaling exponent）Hxy（q）可用来衡量时间序列波动的标度行为特征（scaling behavior）^[1]。当q取不同值时，标度指数Hxy（q）可通过最小二乘法，计算Fq（s）和s对数图的斜率得到。相应的幂律表达式如下：

对于不同取值的q，当Hxy（q）＞0.5时，两时间序列间的交叉相关关系是持续（persistent）的，换言之，从统计意义上而言，一个序列值的增加会使得另一个序列的数值也增加。若Hxy（q）＜0.5，两时间序列间的交叉相关关系是反持续（anti-persistent）的，这意味着从统计的角度而言，一个序列值的增加会使得另一个序列的数值降低，两序列表现出交叉均值回复的特征。若Hxy（q）=0.5，则两序列间不存在交叉相关关系，亦即一个序列值的变动对另一个序列值不会造成统计意义上的任何影响，若两序列为金融时间序列，则该情况表明此时资产价格不可被预测，市场效率最高。

作为广义的交叉相关指数，标度指数Hxy（q）传达了幂律关系的存在。当Hxy（q）的取值独立于q时，两时间序列间的交叉相关关系有单重分型特征，否则有多重分型特征。当x（i）和y（i）是同一序列时，MF-DCCA退化为MF-DFA，当q=2时，MF-DCCA退化为DCCA，且交叉相关指数Hxy（q）与赫斯特指数H类似。

第六步，Renyi指数rxy（q）可用来刻画多重分型本质（Zhou，2008）。

若τxy（q）和q间存在线性关系，则两时间序列间的交叉相关关系是单重分型的，否则则为多重分型。

第七步，通过勒让德变换（Legendre transformation），时间序列的奇异性（the singularity content）可从分形谱（multifractal spectra）fxy（α）得到。

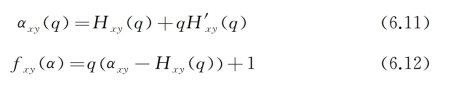
（q）是标度指数Hxy（q）的一阶导数。α为赫尔德指数（Hölder exponent）或奇异力度（singularity strength），描绘了时间序列的奇异性和单重分型特征。分形谱的宽度决定了多重分型的力度（the strength of the multifractality），可通过Δαxy=max（αxy）-min（αxy）求得。分形谱越宽，多重分型的力度越强。

为进一步考察时间序列的多重分型程度（degree of the multifractality），有以下ΔH（Yuan et al.，2009，2012）。

ΔH越大，代表多重分型程度越高，市场波动程度也越高，反之则反。