套期保值与对冲避险的优化方案

假定投资者同时持有期货和现货的头寸，则投资者所持期货和现货头寸的资产组合收益可表示为：

其中RH，t为套期保值资产组合的收益率，Rs，t为投资者所持现货头寸的收益，RF，t为投资者所持期货头寸的收益，γt为套期保值比率。若投资者持有现货头寸的多头，则套期保值比率就是投资者需要卖出的期货合约的数量。基于t-1时期信息集的套期保值资产组合条件方差（波动率）则可表示为：

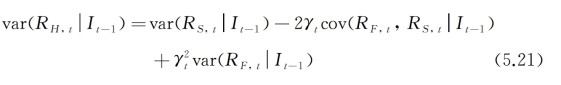
最优套期保值比率（OHRs）为能使套期保值资产组合条件方差（波动率）最小的γt。基于t-1时期信息集的最优套期保值比率可通过5.21式对γt求偏导，并令表达式为零来求得（Baillie and Myers，1991）。

通过GARCH模型估计出的条件波动率可用来计算最优套期保值比率（Kroner and Sultan，1993）。若投资者持有某种资产（比如资产i）的多头，可使用另一种资产（比如资产j）的空头来对冲，则期现价格间的最优套期保值比率为：

其中hsF，t为期现价格收益率的条件协方差，hF，t为期货合约收益率的条件方差。样本外套期保值比率可通过滑动窗口分析法得出。在t时期预测向前一期（t+1期）的条件波动率。预测的条件波动率可用来构建向前一期（t+1期）的套期保值比率，而套期保值比率预测值则可用来构建套期保值资产组合。本书将滑动窗口的长度设定为2 802个观测值，得到向前1 000步的套期保值比率。(www.xing528.com)

图5-4展示了上证综指和恒生指数、上证综指和标普500指数以及恒生指数和标普500指数间向前一步最优套期保值比率。由图5-4可见，ADCC-SGARCH和ADCC-TGARCH模型所产生的最优套期保值比率走势非常接近，而GO-SGARCH和GO-TGARCH模型的最优套期保值比率走势也较为接近。与此同时，GO-SGARCH和GO-TGARCH模型的OHR波动较小，而ADCC-SGARCH和ADCC-TGARCH模型的波动较大。从图5-4的A，B和C三组图形中可以发现，在美联储退出量化宽松货币政策后至美联储进入加息通道前这一段时期，即从2014年年末至2015年年初，以及2015年下半年至2016年年初，三组数据的向前一步最优套期保值比率出现了3次峰值。2015年12月美联储进入加息通道后的半年内，3组数据的向前一步最优套期保值比率经历了较大幅度的上涨。可见在美联储退出宽松型货币政策，货币政策从紧的情况下，投资者均应加大对美股的持有以实现最优的套期保值比率。这与前文对中美股市相关系数在美联储退出量化宽松货币政策以及美联储进入加息通道期间大幅下降，从而有利于投资者配置美股的结论是一致的。

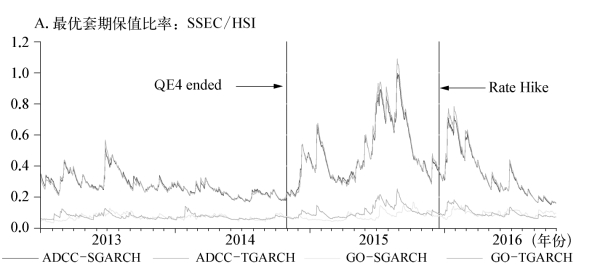
表5-9汇报了根据不同模型形式计算得出的最优套期保值比率间的相关系数。SSEC/SP500该对数列所对应的各相关系数较低，ADCCSGARCH和ADCC-TGARCH模型间的相关系数值接近于1。这和图5-4所示的情形是一致的。

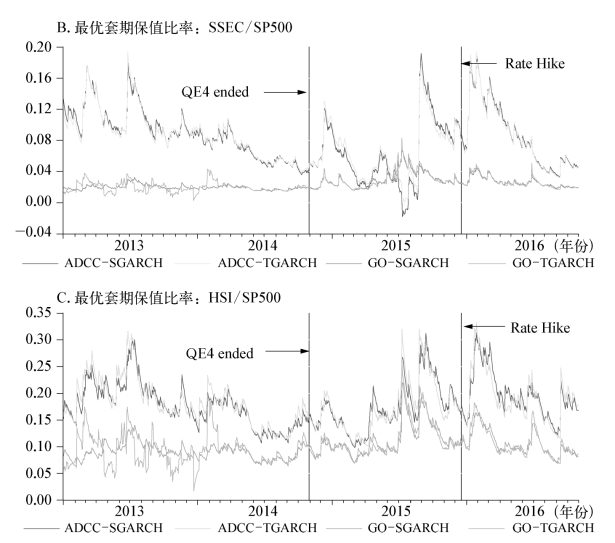
图5-4　向前一步滑动最优套期保值比率

表5-9　不同模型所估最优套期保值比率的相关系数

注：括号内为P值。