GO-GARCH模型实证结果：优化与三项变量的比较

对于GO-GARCH模型，表5-7汇报了旋转矩阵U，混合矩阵A以及参数估计值。因UTU=I，所以旋转矩阵是正交矩阵。因GO-GARCH模型是对因子进行估计，所以估计结果中没有列出参数的标准差。由表5-7可知，对每个因子而言，波动的短期持续性比长期持续性要小得多（α＜β），这和DCC以及ADCC模型估计结果是一致的。单元GARCH模型为EGARCH模型时，根据参数α＞0的要求以及稳定性条件α+（γ/2）+β＜1，模型估计结果较不稳定，这一点和前文一致。

表5-7　GO-GARCH模型估计结果

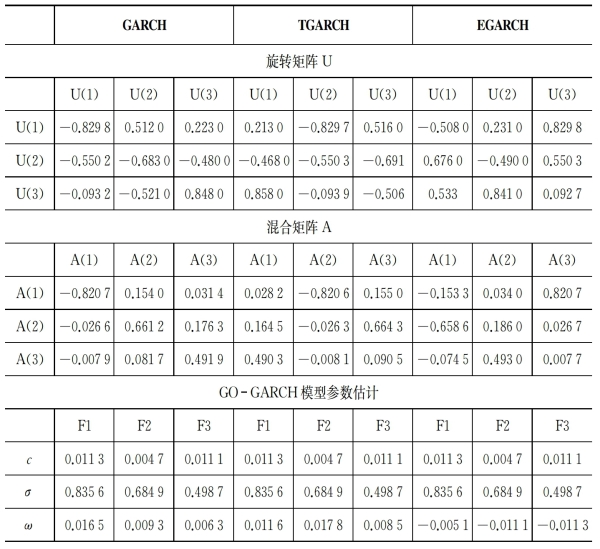
续　表

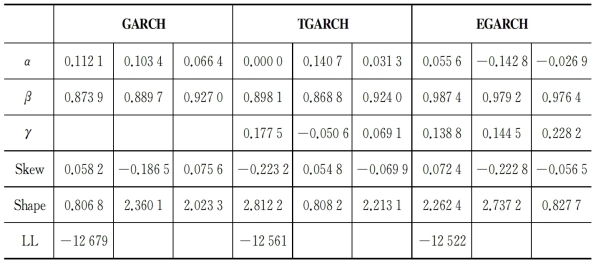
注：该表所得估计结果基于MANIG分布。

由以上估计结果，本书绘制出根据无外生变量的ADCC-GARCH族模型所估计的动态条件相关系数以及由GO-GARCH族模型所估计的条件相关系数走势图。由图5-2可见，ADCC-GARCH族模型中，不同单变量GARCH模型所估计出的动态条件相关系数具有高度一致性。在GOGARCH族模型中，由不同单变量GARCH模型所估计出的条件相关系数走势也非常接近。但ADCC-GARCH族模型与GO-GARCH族模型的条件相关系数走势却存在差异。

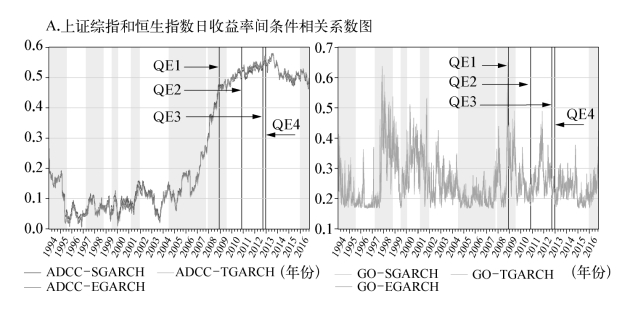
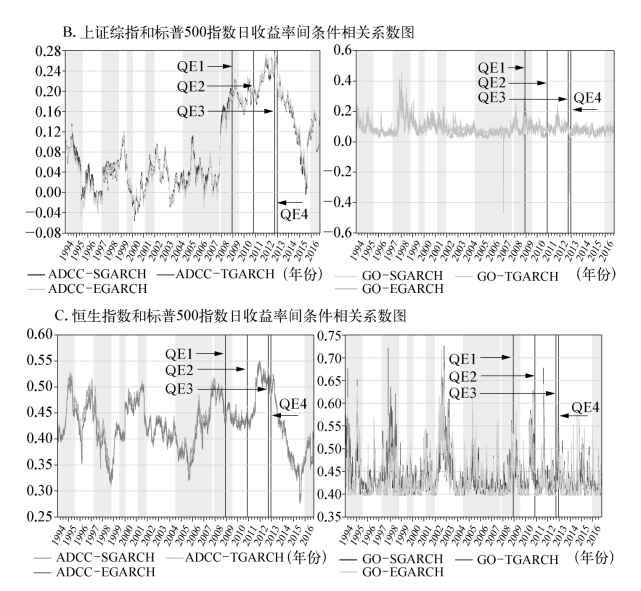
图5-2　上证综指、恒生指数和标普500指数日收益率条件相关系数

注：图中2001年3月至2001年11月，2007年12月至2009年6月的阴影部分为NBER经济周期测定委员会所定义的经济衰退期其余阴影部分为美联储加息区间。四条竖线依次代表美联储推出第一、二、三和四轮量化宽松货币政策的时间点。

ADCC-GARCH族模型的动态条件相关系数波动性较大，上证综指和恒生指数日收益率间的动态条件相关系数从2007年金融危机爆发后便一路上升，从危机前的0—0.2水平左右震荡上升至0.5—0.6水平。可见，2008年金融危机爆发后，内地股市对外开放程度上升，宏观基本面因子对内地和香港的经济和资本市场有着趋同的显著影响。受类似基础经济变量影响的内地和香港经济自然表现出类似或同步的经济水平变动，由此两市场间产生关联性，内地和香港股市的联动性大大增强。

金融危机爆发前，上证综指和标普500指数日收益率间的动态相关系数在-0.04—0.12震荡，相关性较弱，2007年12月—2012年10月，两者的动态条件相关系数迅速上升，从0一路飙升至0.28，可见金融危机的爆发使得中美两国股市处于同一宏观经济大环境中，投资者心理和市场情绪因素趋同。鉴于投资者通常不可能获取市场上的全部信息，因此投资者倾向于跟随其他市场的投资行为，追踪其他市场的动态，当美国投资者面临危机抛售本国股票时，中国投资者在恐慌情绪下也纷纷抛售股票，中美股市间的风险传染加强。从美联储退出量化宽松货币政策至2015年12月美联储进入加息通道前，两市的相关系数迅速下降至零左右，可见两国投资者对美联储货币政策调整的反应和解读差异较大，反映到资产价格上，即表现为两市相关性迅速下跌至零。随后，国内市场逐步消化了美联储货币政策即将调整的信息，两市在美联储加息这一共同事件的刺激下，投资者行为趋同，两市间的动态相关系数随之上升，达至0.16。2015年12月美联储加息尘埃落定后，中美股市受各自国内经济基本面和市场环境、制度所影响，两市间联动性下跌，动态相关系数又从0.16回落至0.08。投资者可抓住两市收益率相关关系为负的特定时刻，持有两市股票，从而获益。(www.xing528.com)

恒生指数和标普500指数日收益率间的动态条件相关系数在金融危机爆发前主要在0.325—0.525的区间内上下波动，且在2007年金融危机爆发前夕呈现出一路上升的态势。金融危机的爆发反倒使两市联动性有所下降，该下跌趋势直至美联储开始执行第二轮量化宽松货币政策时才结束。由此展现出港股和内地股市面对外在冲击时的差异化反应模式。恒生指数和标普500指数日收益率相关系数于第二轮量化宽松货币政策期间飙升至0.55，随着美联储开启第三轮量化宽松货币政策再次下跌，并在美联储步入加息通道前达到最低点（0.275）。这可能是由于美联储在短时间内接连变更量化宽松货币政策，美国国内资金流动性变动剧烈，股市相较港股而言自然展现出不一样的变动特征。随着美联储2015年12月进入加息周期，两市间的联动性在短暂回升后再次下跌。

以上实证结果一方面验证了Ito et al.（1994）关于市场间存在交叉传染的观点^[3]，即中美股市相关性在金融危机爆发和美联储执行量化宽松货币政策（特别是前两轮量化宽松货币政策）期间得到了加强，中美股市间传染效应存在。此外，我们也发现，美联储处在加息周期时，中美股市间的动态相关系数呈下跌的态势，尤其在美国当地时间2015年12月16日，美联储时隔7年再次进入加息通道后，上证综指和标普500指数日收益率条件相关系数迅速从高于0.16的水平滑落至0.08，表明美联储货币政策的调整对中美股市联动有着不可忽视的影响。可能的原因在于，美联储加息往往意味着国际资本、“热钱”回流美国，美元指数上升，人民币汇率贬值预期强烈，中国资本市场面临着资金迅速撤离，流动性大幅下降的局面，中美股市间的相关性自然迅速降低。

GO-GARCH模型的条件相关系数波动则相对小很多，上证综指和恒生指数日收益率相关系数在大多数时期处在0.2—0.3的水平。在1997—1998年东南亚金融危机，2008年全球金融危机以及第二轮至第三轮量化宽松货币政策执行期间，两市相关系数上升至0.6或以上，验证了李成等（2010）以及杨雪莱和张宏志（2012）关于市场间交叉传染的论点，表明金融危机所带来的市场传染效应使得内地和香港股市的相依性有所上升；对上证综指和标普500指数日收益率而言，除了在1997—1998年亚洲金融危机，2007—2008年金融危机以及2011—2012年欧债危机期间两市的条件相关系数越过了0.2水平，其余绝大多数时候两市相关系数均维持在略高于零的低位水平；恒生指数和标普500指数日收益率间的条件相关系数波动性比前两者要大，且与ADCC模型的结论类似，恒生指数和标普500指数日收益率间相关性也强于其他两者（恒生指数和标普500指数日收益率相关系数平均大约在0.5左右），尤其强于上证综指和标普500指数日收益率间的相关性。可见，香港股市相对于内地股市，与美国股市的关联性更强，对外界冲击的反应更为灵敏。2015年12月美联储货币政策的中性化（在这里货币政策中性化指基准利率从极低利率水平向常规利率水平变动）使得两者间相关性有下降的趋势。由以上分析可以看出，美联储每轮加息周期以及美联储执行新一轮量化宽松货币政策所带来的美元回流、汇率波动以及市场预期调整，对中美股市的相依性都会产生一定程度的影响。因此我们可得出结论，美联储货币政策调整对中美股市的相关性以及投资者的投资策略制定都有着不可忽视的影响。

参考Basher and Sadorsky（2016），本书于表5-8中给出不同模型所估条件相关系数的相关系数。对于每一对股指日收益率，ADCC族模型和GO-GARCH族模型所估计出的条件相关系数间的相关性非常弱，其中相对而言最高的是ADCC-SGARCH和GO-SGARCH模型所估条件相关系数的相关性（0.045 8）。另一种进一步探究该问题的方法是绘制“信息冲击相关系数曲面”（news impact correlation surface）。鉴于各冲击对因子产生各自独立的影响，而信息冲击曲面是各因子独立信息冲击曲面的结合，结合混合矩阵A，可构造潜在资产因子曲面方程的动态效果。鉴于本书重点考察对象是上证综指和标普500股指日收益率间的联动性，因此我们绘制出不同模型框架下SSEC/SP500的条件相关系数曲面图。

表5-8　不同模型所估条件相关系数的相关系数

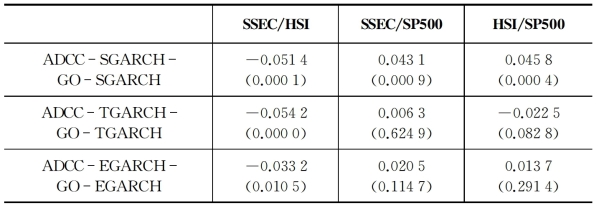
注：括号内为P值。

在ADCC-SGARCH模型框架下（图5-3a），从z-1坐标轴（SSEC）来看，上证综指和标普500指数的条件相关系数曲面从0.3下降至-0.3。与之相对，从z-2坐标轴（SP500）来看，条件相关系数曲面从-0.3逐步上升至近0.6。因此，不同冲击对上证综指和标普500指数日收益率间的相关性有着非对称的影响。在ADCC-TGARCH模型框架下，条件相关系数曲面表现出相似的形态和特征（图5-3b）。

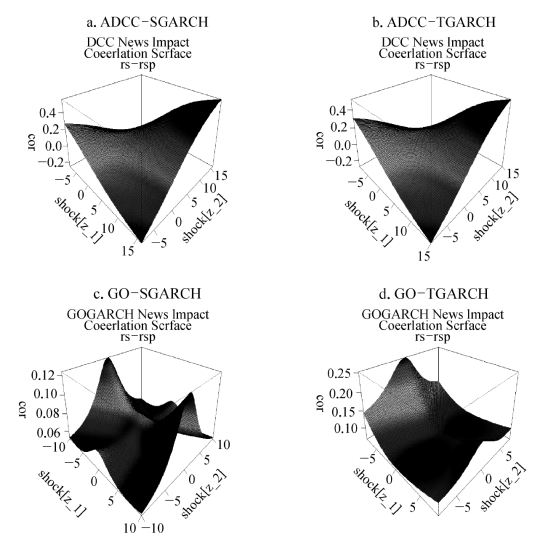
图5-3　上证综指和标普500指数日收益率的信息冲击相关系数曲面

注：rs代表上证综证的日收益率，rsp代表标普500指数的日收益率。

在GO-GARCH模型框架下，条件相关系数曲面的形态发生了巨大变化。在ADCC模型框架下，曲面呈现出凸的特征，但在GO-GARCH模型框架下，整个曲面更多表现出凹的特征。由GO-SGARCH模型所得条件相关系数曲面可知，从f-1坐标轴来看，因子1和因子2的相关系数从0.04上升至0.06，随后又降至0.04。从f-2坐标轴来看，外来冲击使两者相关性从0.04上升至0.14，随后又降低至0.04。由GOTGARCH模型所得条件相关系数曲面与之有一定区别。从f-1坐标轴来看，因子1和因子2的相关系数从0.14降至0.05，随后又缓慢升至0.10。从f-2坐标轴来看，外来冲击使两者相关性从0.10升至0.15，随后又下降至0.10。相较于ADCC模型，GO-GARCH模型的信息冲击相关系数曲面对称性更强，无明确方向（零附近）的冲击使两市间相关性上升。这是因为在GO-GARCH框架下，冲击是附属于因子的，而GOGARCH模型的因子都是正交的。