动态条件相关系数（DCC-GARCH）模型及应用分析

标准GARCH模型未考虑资产间的相关性（协方差）是否发生变化。本部分采用Engle（2002）提出的Dynamic Conditional Correlation模型，通过采用不同形式的单元GARCH模型，考察金融市场变量间波动溢出及其动态相关性，从而进一步分析市场间波动效果溢出效应。Engle（2002）的两元DCC模型可简要表述如下：

假定收益率向量rt服从rt～N（μ，Ht）分布，设定条件协方差矩阵服从Ht=DtRtDt形式。其中Dt为对角元素为收益率序列标准差的对角矩阵，Rt为各收益率序列经单元GARCH模型拟合后得到的标准化残差的条件相关矩阵。DCC模型的估计过程可分为两步：第一步，使用单元GARCH模型得到各收益率序列的条件方差q1，t和q2，t；第二步，设定条件

相关矩阵为如下形式：

其中Qt具备如下形式：(www.xing528.com)

z1，t-1和z2，t-1分别为从两个单元GARCH模型中得到的各收益率序列的标准化残差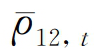，12，t为两标准化残差的无条件相关系数。由此我们可得到条件相关系数如下所示：

Cappiello et al.（2006）基于DCC模型和GJR-GARCH模型，通过在单元GARCH模型波动方程中加入非对称项，提出了ADCC模型的架构。非对称项也可被视为杠杆效应项，可用来测度这样一种常见的现象：金融资产价格下跌对波动的强化作用大于金融资产价格上升对波动的强化作用。这也可被解读为坏消息比好消息对市场的冲击更大。ADCC模型中，动态Qt变为如下形式：

其中A，B和G为n×n参数矩阵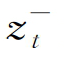，为以零为门限的标准化残差序列。当其小于零时取zt，大于零时取零。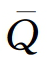和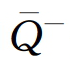分别为zt和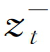的无条件相关系数矩阵。