单元GARCH族模型的优化方法

为测定金融资产收益率波动效应，Engle（1982）提出了ARCH模型，随后Bollerslev（1986）又进一步提出了GARCH（Generalized Autoregressive Conditional Heteroskedasticity）模型，基本的GARCH模型未考虑正负不同信息的非对称性。Glosten，Jagannathan and Runkle（1993）在基本GARCH模型条件方差方程中加入负冲击的杠杆效应，得到GJR-GARCH模型，以此考察和测度收益率冲击对波动影响的非对称效应。Zakoian（1994）首次提出门限GARCH（TGARCH）模型，以测度收益率冲击对波动可能存在的非对称影响，如下式所示。

方程（5.1）为均值方程，Rt为市场从第t-1日至第t日的每日收益率，Φt-1为第t-1日的市场信息集，方程（5.2）为条件方差方程。该模型假定正负残差εt对条件方差的冲击存在非对称性，对条件方差ht的正和负冲击是不同的。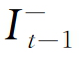为示性函数，当εt＜0时，该值取1，否则为0。当γ为零时，TGARCH模型退化为普通GARCH模型。

Nelson（1991）提出了刻画收益率冲击对波动影响非对称效应的另一种GARCH模型，为Exponential GARCH（EGARCH）模型，具体模型形式如下：(www.xing528.com)

相关参数的解读同TGARCH模型类似，γ项仍为测定非对称效应的参数。EGARCH模型相较于普通GARCH模型和TGARCH模型，其优势在于自动保证条件方差为正。下文我们将普通GARCH模型，TGARCH模型以及EGARCH模型分别作为动态条件相关（DCC）模型框架下的单元GARCH模型，估计DCC模型的动态相关系数。