样本选择和模型描述的优化策略

本部分选取上证国债指数，上证公司债指数，上证企业债指数。因债市的交易相对股市而言，每日收盘价波动相对较小，因此，参照Alizadeh et al.（2002），本章我们将基于日内对数最高价和对数最低价之差计算得出的日内对数价格变动区间（Range）考察美联储货币政策对我国债市的影响（但为叙述简便，这里的对数价格变动区间后文将统一简称为收益率）。上证国债的样本区间为2003年1月2日至2018年2月21日，上证公司债的样本区间为2008年1月2日至2018年2月28日，上证企业债的样本区间为2003年6月9日至2018年2月21日。

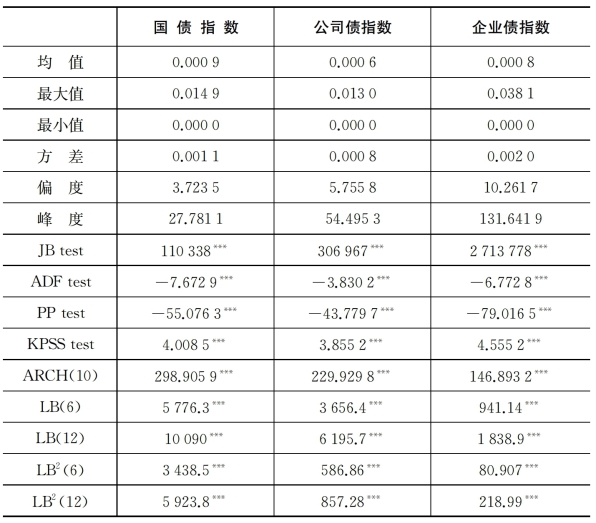
由表4-7可见，我国国债指数，公司债指数以及企业债指数日内对数价格变动区间皆接近于零，偏度均为右偏，峰度均大于3，序列均不为正态分布，序列皆平稳，但存在异方差性，序列有ARCH效应，表明使用GARCH类模型进行拟合是适合的。

表4-7　上证国债指数，公司债指数和企业债指数描述性统计结果

注：“Shibor-3M”，“FR007”，“TB-3M”分别代表3个月Shibor利率，3个月银行间回购定盘利率以及美国3个月国债收益率，其他符号与表4-1类似。(www.xing528.com)

对于控制变量的选取，我们首先将美联储货币政策调整划分为扩张周期（expansionary）和紧缩周期（contractionary），扩张周期为美国当地时间2003年1月2日至2003年6月25日，2006年6月30日至2008年10月16日，紧缩周期为美国当地时间2003年6月26日至2006年6月29日，2008年12月17日至样本期结束。因此，我们考虑在EGARCH模型中加入美联储政策周期调整的虚拟变量，当美联储处于紧缩周期时，该变量取1，当美联储处于扩张周期时，该变量取0。与此同时，我们参照郦金梁等（2012）的做法，将每日交易量分解为预期部分和冲击部分。具体方法如下，

其中a为常数，b为滞后一阶的对数交易量的系数，et为残差项，我们将残差的估计值定义为交易量的冲击（innovation）部分Δυolt，将对数交易量减去交易量的冲击部分得到交易量的预期部分Δυolt。

将交易量的冲击部分和交易量的预期部分作为控制变量纳入EGARCH模型的均值方程和方差方程中，并将交易量的冲击部分和预期部分分别与美联储货币政策相乘得到交乘项，一并纳入EGARCH模型的均值方程和方差方程中。均值方程采用常数项加上滞后一阶的自回归项，再加上外生变量的形式。具体模型如下所示。其中式（4.14）为加入外生变量的均值方程，式（4.15）和式（4.16）为方差方程。式（4.15）为加入外生变量的EGARCH模型形式，式（4.16）为加入外生变量的TGARCH模型形式。φi，φj以及ψk为均值方程，EGARCH模型和TGARCH模型外生变量的系数。