如何进行一致性检验：详细指南

从理论上分析得到：如果A是完全一致的成对比较矩阵，应该有aijajk=aik。

但实际上在构造成对比较矩阵时要求满足上述众多等式是不可能的。因此退而要求成对比较矩阵有一定的一致性，即可以允许成对比较矩阵存在一定程度的不一致性。由分析可知，对完全一致的成对比较矩阵，其绝对值最大的特征值等于该矩阵的维数。对成对比较矩阵A的一致性要求，转化为要求A的绝对值最大的特征值和该矩阵的维数相差不大。

检验成对比较矩阵A一致性的步骤如下：

计算衡量一个成对比较矩阵A（n＞1阶方阵）不一致程度的指标CI：

式中λmax是矩阵A的最大特征值。

从有关资料查出检验成对比较矩阵A一致性的标准RI，RI称为平均随机一致性指标，它只与矩阵阶数n有关。随机指标如表10-1所示。按下面公式计算成对比较矩阵A的随机一致性比率CR：CR=。

表10-1随机指标表

判断方法如下：当CR＜0.1时，判定成对比较矩阵A具有满意的一致性，或其不一致程度是可以接受的；否则就调整成对比较矩阵A，直到达到满意的一致性为止。(www.xing528.com)

对上例的矩阵：

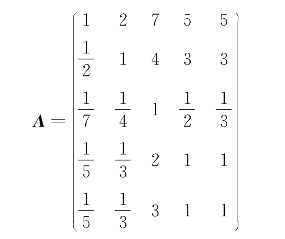
计算得，查得RI=1.12，

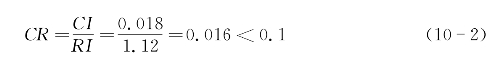
这说明A不是一致阵，但A具有满意的一致性，A的不一致程度是可接受的。此时A的最大特征值对应的特征向量为U=（-0.8409，-0.4658，-0.0951，-0.1733，-0.1920）。这个向量也是问题所需要的。通常要将该向量标准化，使得它的各分量都大于零，各分量之和等于1。该特征向量标准化后变成U=（0.457，0.263，0.051，0.103，0.126）T。经过标准化后这个向量称为权向量。这里它反映了决策者选拔干部时，视品德条件最重要，其次是才能，再次是群众关系、年龄因素，最后才是资历。各因素的相对重要性由权向量U的各分量所确定。

在实践中，可采用下述方法计算成对比较矩阵A=（aij）的最大特征值λmax（A）和相应特征向量的近似值。

定义可以近似地看作A 的对应于最大特征值的特征向量。

计算

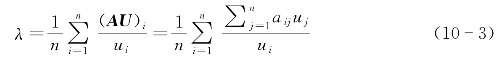
λ可以近似看作A的最大特征值。实践中可以由λ来判断矩阵A的一致性。