【摘要】：比较同一层次中各因素关于上一层次的同一个因素的相对重要性，构造成对比较矩阵。通过计算，检验成对比较矩阵的一致性，必要时对成对比较矩阵进行修改，以达到可以接受的一致性。在符合一致性检验的前提下，计算与成对比较矩阵最大特征值相对应的特征向量，确定每个因素对上一层次该因素的权重；计算各因素对于系统目标的总排序权重并决策。
本小节介绍定性分析时经常使用的层次分析法（analytic hierarchy process），来了解如何通过层次分析法将定性问题定量化。
层次分析法简称AHP法，是美国运筹学家沙旦于20世纪70年代提出的，是一种定性与定量分析相结合的多目标决策分析方法。特别是将决策者的经验判断给予量化，引入决策系统。
AHP法基本理论是先对问题所涉及的因素进行分类，然后构造一个各因素之间相互连接的层次结构模型。因素分类：一为目标层，表示问题所要达到的目标因素；二为准则层，这是衡量目标能否实现的标准；三为子准则层，是准则层的细分（准则层可不限于一层，只要最终把问题剖析清楚即可）；四为方案层，指实现目标的方案、方法、手段等。按目标到方案自上而下地将各类因素之间的直接影响关系排列于不同层次，并构成一层次结构图。根据层次结构图确定每一层的各因素的相对重要性的权数，直至计算出措施层各方案的相对权重数。依此可对各方案进行优劣排序，最后作出选择。对于复杂的问题，可分为总目标层、子目标层、准则层、子准则层、方案层或层次更多的结构。
层次分析的四个基本步骤：
（1）在确定决策的目标后，对影响目标决策的因素进行分类，建立一个多层次结构。(www.xing528.com)
（2）比较同一层次中各因素关于上一层次的同一个因素的相对重要性，构造成对比较矩阵。
（3）通过计算，检验成对比较矩阵的一致性，必要时对成对比较矩阵进行修改，以达到可以接受的一致性。
（4）在符合一致性检验的前提下，计算与成对比较矩阵最大特征值相对应的特征向量，确定每个因素对上一层次该因素的权重；计算各因素对于系统目标的总排序权重并决策。
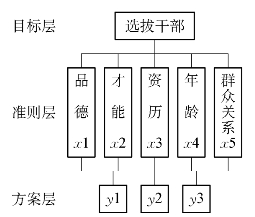
图10-1层次结构图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
