边际结构模型及其灵活设定和估计方法

如上文所述，边际结构模型针对Ypotential建模。这里，Ypotential指的是A的不同取值串下Y的潜在取值。需要指出的是，所谓的潜在取值，指的是如果“所有的人”都接受了特定A的取值串的情况下在Y上的取值，而不是我们看到的那些A的取值真的为特定取值串时Y的取值。例如，上面提到的三个时间点，A有八种不同的潜在取值串，那么Ypotential就有八种情形，分别代表着“如果数据中的所有人”的A取八种中的任意一种时Y的取值。

前面章节中也遇到过类似的问题。在简单随机实验中，我们手里有的数据是实验组中分析对象的Y的取值和控制组中分析对象的Y的取值（期望值）。而我们想知道的是，如果所有人都进入实验组的话，Y的取值（期望值）是什么，以及如果所有人就进入控制组的话，Y的取值（期望值）是多少。当时，我们采用了加权的方法完成这一工作，即针对实验组中的个体进入实验组的概率，取其倒数来估计如果所有人都是在实验组的话Y的期望值。同理，针对控制组也可以利用个体进入控制组的概率的倒数进行加权计算。这里，针对处理变量随时间变化的情况，我们也可以采用同样的分析策略，只是这里我们的加权办法较之以前更为烦琐。由于A是一串处理效用取值，因此，在控制混淆变量L的取值历史Lt的情况下，A取值为特定处理历史At的概率可以写成

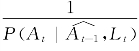自然，我们要加权的话，就可以使用P（At|Lt）的倒数。为了估计出P（At|Lt），我们就需要对等式右边的各项进行估计。P（A1|L1）是用L1来预测A1的概率，如果A1是一个二分变量，我们可以拟合logistic回归模型获得P（A1|L1）的估计值同理，P（A2|A1，L2，L1）可以用logistic回归模型来获得其估计值，其中A2为响应变量，A1、L2和L1为自变量。依次类推，后面每一项我们都能够估算出其估计值。那么，针对时间点t而言，我们估计出的概率为在这个时间点上的加权权重为，整个针对一串A取值At的总的加权W就可以写成

在实际的计算过程中，W有可能出现极值。这是因为分母是一系列概率的乘积，而概率是取值0～1之间，因此乘积项越多，最后的取值越小，那么权重就会越大。由于极端权重会将最后的估计结果向大权重对象方向拉，因此我们通常希望尽可能地避免大权重的出现。为此，一个解决办法就是可以在分子上乘以一个数来尽可能平衡W的取值。这里，我们可以得到新的稳定权重（stabilized weight，简写为Ws，其中s表示稳定的意思），如下：

相比于上面的权重表达式，稳定权重在分子部分增添了一个连乘积，这一乘积中的单独的每一项是各个时间点的At依据前面时间点一系列A的取值Ai-1预测的概率值。之所以这一项可以起到稳定权重的作用，是因为如果分母过小的话，分子也肯定同方向的变小，从而不至于出现过分大的权重值。当然，除了上面表述的Ws之外，我们也可以在分子的连乘积内放入基线的混淆因素L1，这起到类似的效果：(www.xing528.com)

上述权重的表达式本质上就是各个时间点上的倾向值估计值的乘积，其中用来估计倾向值的是时间点t及其之前的各时间点的混淆变量L，以及时间点t之前的A的取值历史。正因为如此，我们需要正值假设，即要求分母相乘的各项不能为0，否则只要有一项为0，分母即为0，后续的分析便无法进行了。

上面介绍了基本的加权方案，下面介绍一下模型的设定问题。在边际结构模型中，模型的形式设定可以比较灵活。例如，我们可以认为各种潜在状态下的Y的取值Ypotential的期望值为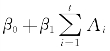。此时，我们实际上看的是一共个体在所有时间点内，A取值为1的总数。当然，也可以设定模型，认为特定时间点m之前的处理效应与m之后的处理效应不同，即Ypotential的期望值设定为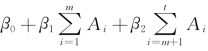。最后，我们也可以在模型中放入其他不随时间变化的变量，并设定其与各个时间点的A产生交互效应，不一而足。

需要说明的是，如果数据结构比较简单，我们实际上可以不采用加权的办法来估计边际结构模型。这里采用的方法是利用g 估计的手段来估算Ypotential的期望值。这一估算过程依据的公式被称为g-formula（这里的g表示广义generalized的意思）。这个公式表示起来很简单，其将Y的分布函数写成处理变量历史A和混淆变量历史L的函数。由于我们关心的是Y的分布如何随着A改变而改变（亦即A对Y的影响）。此时，g-formula将给定A时Y的分布函数写为

如果我们能够利用数据估算出第t个时间点的Y值如何受到t以及之前一系列A的取值和L的取值的影响，并同时能够估算出每个时间点混淆变量L如何受到之前一系列A的取值和L的取值的影响，就能够直接用非参数的方法写出f（Yt|At） ，自然也就能够计算出E（Yt|At），进而估计边际结构模型。例如，如果有两个时间点的话，我们有f（Y2|A1，A2）=|A1，A2，L2，L2）×f（L2|A1，L1）×f（L1）。