随时间变化的处理效应简介

在本章中，我们将介绍两种方法来分析随时间变化而变化的处理变量对于响应变量Y的因果效果。在前面介绍的各种方法中，我们的处理变量通常是在某个特定时间点测量的。例如，在个体进入到一个研究设计中后，一些人被分配到实验组，一些人被分配到控制组，分配完以后，各自就留在相应的组中间，每个人的处理变量的取值就固定了，或者1，或者0。但是，一些现实的社会问题涉及更为复杂的情况。比如，如果我们关心的处理变量是所在居住小区的类型（可以简单划分为好的小区和差的小区，分别取值为1和0）对于个体高考成绩的影响，那么在一个人参加高考之前，可能有一系列的搬迁。此时，处理变量就涉及随时间变化而变化的情形。一个人可能搬迁过两次，那么处理变量就有三个状态。假设这个人出生时居住在一个不是很好的小区，但是随着时间的推移，家庭经济状况逐渐好转，后续小学阶段和中学阶段搬进了好的小区，那么处理变量取值“串”为0 1 1。同理，如果一个人一开始住在一个好的小区，但是逐渐家道中落，则他或者她的处理变量的取值可能就是1-1-0，依此类推。

随时间变化而变化的处理效应之所以重要，是因为它衡量了处理变量的潜在变化对于响应变量的影响。例如，在上面谈到的居住小区的问题中，如果我们只是看高中阶段的小区类型，那么小时候一系列生命历程下的居住小区状态就被忽略了。但是形塑一个人学习习惯的关键时期可能恰恰是高中以前的生命历程阶段。因此，我们需要考察个体在早些时候的居住环境，这种居住环境的影响可能是持久的，甚至是比后续的居住环境影响更大。因此，考虑随时间变化的处理变量非常重要。实际上，在公共卫生和医学研究中，此类方法也是有很大的用武之地的。例如，病人的服药剂量有可能随时间变化而变化。一个病人入院10天，每一天的药量会根据其表现不断改变。此时，为了很好地把握药物效果，我们需要考虑这10天处理变量的变化情况，以及这种变化对病人出院前的状态Y的影响。

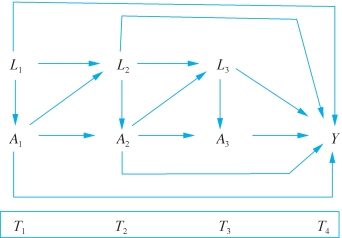
显然，一旦把时间因素引入进来，因果推论过程中的混淆偏误的作用情况就会非常复杂。时间通常用T来表示，为了避免误解，我们在本章中用A来指代处理变量，L指代潜在的混淆因素，Y指代响应变量。基于这些变量，我们可以假想如图12-1所示情况。

(www.xing528.com)

图12-1　随时间变化的处理变量图示

如图12-1所示，假设有四个时间点，T1是基线状态，在这个点上我们观测到处理变量A1和混淆变量L1的取值，其中A1的取值受到L1的影响。在T2这个时间点，L2受到L1和A1的影响，A2则受到A1和同时期的L2的影响。依此类推，在T3这个时间点，L3受到之前的L2和A2的影响，同时A3受到之前A2和同时期L3的影响。最后在T4这个时间点，我们测量了响应变量的取值Y。在这个图示中，处理变量涉及一系列取值“串”A1 A2 A3。同时，混淆变量也是随时间变化的，因此同样呈现出一连串的取值L1 L2 L3。和前面谈到中介分析时的情形类似，我们这里不能通过简单的控制L1、L2和L3来分析A1 A2 A3对Y的影响。例如，L3代表了A3和Y之间的一个混淆因素，因此为了分析A3对于Y的影响，需要控制L3。但是，L3本身又是A2对Y影响的中间因素，如果控制了L3，A2对于Y的影响就会被低估。再则，L3本身称为碰撞变量（collider），如果我们控制了L3，L2和A2本来因为控制L2而被打断的联系又被恢复了。此时，A2对Y的影响受到了A2←L2→Y这条线的混淆。

总之，在随时间变化的处理效应分析过程中，我们不可避免地进入到一个两难境地。对于那些随时间变化而变化的混淆变量，我们控制他们也不是，不控制他们也不是。此时，需要采用一些特殊的处理办法。在使用这些方法之前，有一些通用的前提假设需要满足。这些假设可以被看成是传统因果推论假设在随时间变化的因果关系分析中的一个扩展。