在社会科学研究中,固定效应模型使用的越来越多(Allison,2009)。尤其经济学的很多经验考察,都会采用固定效应。所谓固定效应,顾名思义,就是通过变量控制的手段将一些需要考虑到的具有混淆效应的变量“固定”起来(见图8-1)。
固定效应和因果关系的估计是怎么结合起来的呢?这个问题的答案可以用上面的图示来说明。假设处理变量D和响应变量Y之间的关系是我们关心的问题。那么我们知道,一些混淆变量有可能同时影响了D又影响了Y。常规的操作是把这些混淆变量找出来,然后在一个回归模型中控制起来,这个是常规的办法。但问题在于,我们需要控制的混淆变量有可能很多,无法穷尽。或者虽然我们能够想到某些混淆变量,但是数据中缺乏相关的测量。比如,在研究上大学对收入的影响的时候,什么因素会同时影响一个人上大学的概率和收入的高低呢?这种混淆因素的列表可以很长。在某一项具体的研究中,我们经常有一种顾虑,生怕遗漏了潜在的混淆因素。
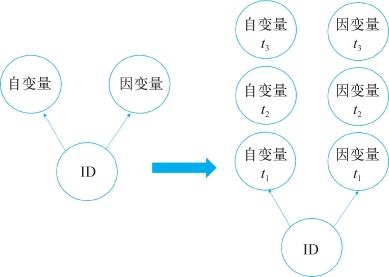
图8-1 固定效应示例
这时候,我们会希望有一个一劳永逸的办法,即能够有一个变量把潜在的混淆因素一网打尽。这个变量实际上就是被研究对象在一个数据中的ID。无论是直接观测到的还是无法直接观测到的混淆因素,所有变量的取值都是跟随着个体ID来的,故而ID和所有的变量都是高度相关的。比如说1、2、3是三个被研究对象的ID,这三个人对应的性别取值为男、女,女,对应的年龄取值是30、40、50等。可见,所有这些混淆变量的取值组合最复杂的情况下也只能对应特定的ID。此时,就算我们有很多混淆变量,甚至有很多没能够直接测量的混淆变量都没有关系,因为无论这些混淆变量的取值如何彼此组合,最终对应每种组合都是一个特定的ID。很显然,如果我们把ID给控制起来,根本不用担心混淆变量的问题。
但是,是否能够这样操作取决于数据的性质。比如上图左边所示的截面数据情况,是否我们把ID控制起来,处理变量和响应变量的关系就不受混淆因素影响了呢?理论上如此,但是经验上我们却不能这样做。这是因为我们在把混淆变量的组合给控制起来的同时,控制ID也把处理变量和响应变量的各种取值组合控制起来了。从某种意义上讲,控制ID也就固定了“一切”取值。换句话说,我们拟合一个模型,然后把ID作为控制变量给控制起来之后,实际上相当于每一个ID下面只有一个观测值。也就是说,对应于处理变量的每个取值水平,我们只拿了一个观测值去做回归,这个时候当然什么都得不到,因为自由度完全不够用。在常规的截面数据中,类似的问题便会发生。
但是,如果我们手里的是一个历时性的数据,情况就有所不同了。在一个历时性的数据中,每一个ID下面,就不是一个观测值,而是一串观测值。具体的数据结构如上图右边所示。比如一项研究中,我们针对每个分析对象连续观测四年,这样每个ID下面有四个历时性观测值了。那么,即使我们控制了ID,也可以探究处理变量和响应变量的关系。比如,我们只看ID=1的话,ID下的处理变量和响应变量都还是有自己的变动过程。针对上面的例子,至少处理变量和响应变量都有四年的变动趋势。这时,我们控制了ID以后,还是可以分析D和Y各自四年的变化之间有什么“共变”关系。反观传统的截面数据的话,我们对每个人的观测点只有一个,针对ID=1,D就一个固定的值,Y就一个固定的值。如果我们只有两个固定的取值,自然没有什么相关关系可以计算,毕竟D和Y没有变化,它们都不再是变量。而这些问题在历时性的数据中就不再是问题了。
那么,我们可以进一步看一下ID所控制起来的是哪些因素。简单地说,固定效应通过固定ID的方式所控制起来的因素,是那些“不随时间变化的个体特征。”比如,我们控制了ID,那么这个被分析对象的性别特征(比如男性)便被控制起来了。由于性别不会随着时间变化,所以在一个特定的数据集里面,我们会发现,这个人的性别变量的取值在各个年份都是一样的。男性总是男性,四年的取值是一样的。除了性别之外,还有很多不随时间变化的因素,比如种族。在我们控制了ID之后,类似于这种不随时间变化的因素,无论看得到还是看不到,都被控制起来了。换句话说,固定效应甚至能够将那些看不到的“不随时间变化”的混淆因素固定起来,这是其他因果推论手段通常无法完成的。这个特点对于经验研究者非常具有吸引力,因为有大量的混淆变量跨时点变化的幅度很小,我们便可以近似地认为固定效应也将这种混淆变量控制起来了。总结一下,在固定效应模型中,通过控制了ID,我们实际上控制的是那些不随时间变化的个体特征,无论观测得到还是观测不到,都被控制起来了。
但是,固定效应却无法控制那些随着时间变化的混淆因素。这实际上很好理解。在固定效应中,我们关心的是,平均而言,处理变量的变动趋势如何和响应变量的变动趋势产生关联。但是如果混淆变量本身也随着时间变化而变化,且变动模式与处理变量保持一致,那么无论我们通过固定效应发现了何种处理变量和响应变量之间的关联性,都无法排除混淆因素的效果。举例而言,假设混淆因素为Z,且Z的变化趋势和D一致,那么在图8-2中,D和Y的负相关有可能是由于Z的干扰造成的。换句话说,Z和D正相关(变动趋势一致),Z和Y负相关(变动趋势相反),那么自然,D和Y彼此之间即使没有什么实质性的关联,其变动趋势也为负相关。
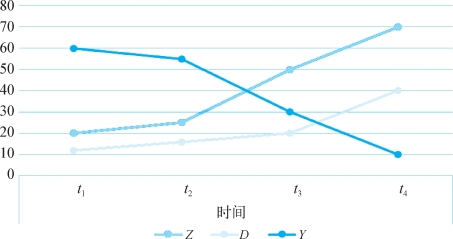
图8-2 随时间变动的混淆误差
固定效应的具体计算过程很简单。具体而言,有两种办法。一种是,如果有两个时间点的话,计算y在这两个时间点之间的变化,即做了一个差值运算。假设模型可以写为(i表示个体,t表示时间,αi表示个体的效应,λt表示时间效应,Xit是控制变量):
![]()
假设时间点从0到1,很显然,在时间点0,我们有:
![]()
在时间点1,我们有:
![]()
那么,通过计算他们的差值,我们就把代表个人特征的αi约掉了,从而得到(https://www.xing528.com)
![]()
另外一种计算固定效应的方法,就是中心化运算,即每个变量减掉了它相应的均值。此时,针对响应变量的均值,我们有
![]()
用yit减掉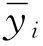 ,我们同样可以消掉代表个人效果的αi,即
,我们同样可以消掉代表个人效果的αi,即
![]()
实际上,对于大多数的因果推断问题而言,固定效应模型是一个很好的选择。如果研究者有理由认为,随时间变动的混淆变量很少,而大部分的混淆变量来自不随时间变动的那些变量时尤为如此。社会科学研究者通常还会纠结于究竟是选择固定效应还是选择随机效应。这方面也有一些计量经济学的检验方法。但是从因果推论的角度看,固定效应和随机效应有不同的模型表达方式,因此随机效应有可能无法起到控制混淆因素的作用。例如,在传统的随机效应模型中,我们有
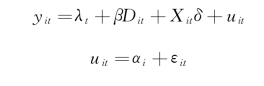
这里的uit代表随机扰动项,在随机效应模型中,这一随机扰动项被分解为两部分,一部分是个体之间的变异水平αi,一部分是个体内部不同时间点的变异水平εit。从这个角度来看,随机效应模型和固定效应模型的区别就显现出来了,其区分的关键在于我们如何定义αi。
在固定效应模型中,αi代表的是每一个个体的ID,张三的ID是1,李四的ID是2,等等。这个ID是一个固定了的数字,是一个有实际意义的具体值,不被看作一个变量。正因为αi是一个定死的数,不随时间变化而变化,我们才能够采用计算差值或者中心化的手段将其去掉,这是固定效应的逻辑。但是随机效应下,每个人是被看作一个总体的样本中的一个代表。个体所带来的,是方差的差异。此时,ID就不是一个定死的固定值,而是一个变量,它有自己的分布和方差。之所以有自己的方差,是因为下一次抽样的时候,ID信息可能就变了。因此,如果是看随机效应的话,相当于做了一个方差分解的工作,一部分方差来源于个体之间的差异,一部分方差是来源于个体内部的差异。这就类似于,我们看一个数据集中Y的总的变化,一部分的变化原因来自人和人不一样所带来的Y的变异,还有一部分原因来自平均而言,特定的对象随着时间变化所体现出的Y的变异,这是两种来源的方差。将其区别开实际上就是一个方差分解:组间的方差就是人和人之间的方差,组内的方差,就是特定的人随着时间变动的方差,这是随机效应的基本思路。由于随机效应不是把每个个体的ID当成固定的值,而是看作一个更大的总体中抽样得来的观测点,所以在作随机效应的时候,作的本质上是方差分解。但是,由于我们不再把αi看成一个可以代表所有不随时间变化的混淆变量的代表,随机效应模型很难帮助我们控制潜在的混淆因素的影响,自然也不太能够帮我们进行因果推断。从这个角度而言,至少就因果推断而言,固定效应要优于随机效应。
当然,这里也加一句,固定效应虽好,但也不是无懈可击。例如,固定效应由于消掉了αi,因此无法提供针对不随时间变动的变量的系数估计。此外,固定效应会放大测量误差的影响,这些都是我们应当注意的地方。
在R里面,固定效应的分析可以用以下代码实现。这里我们采用世界价值观的调查,控制的固定对象是国家ID,即控制了国与国之间潜在的和观测到的混淆因素。相关的经验发现的解释和传统的线性回归一样,这里不再赘述。需要注意的是,下面的代码前半部分是直接控制了国家ID,将其作为哑变量放进模型。后半部分的代码使用的是特定的固定效应估计程序。两个分析步骤的结果是一样的。但是,如果ID变量太多,将其作为哑变量放入模型会带来自由度的极大损耗。在样本有限的情况下,还是建议读者慎用。
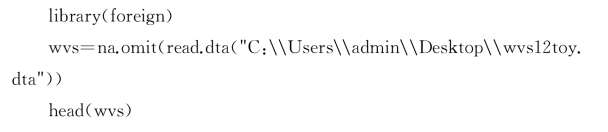

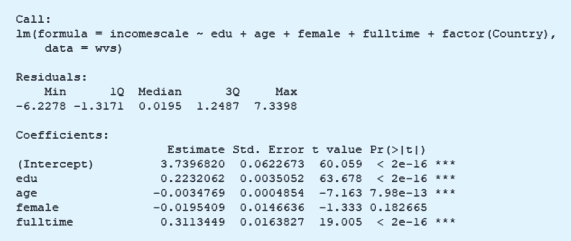

在STATA中,我们也可以进行固定效应分析,代码如下。经验结果和上面的一致,这里不再赘述。

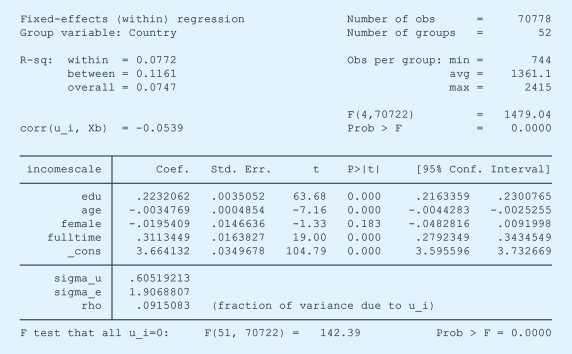
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




