如何选择带宽并进行稳健性检验

目前为止，我们已经介绍了如何利用回归断点设计进行因果关系的分析。在这一部分，我们将介绍两个辅助性工作。第一个工作是带宽的选择。第二个工作是对结果的稳健性进行评估。

对于第一个问题，首先需要明确，什么叫带宽呢？带宽就是我们在一个回归断点设计中，从临界点c往左往右各挪动的距离。在回归断点设计中，带宽的选择很重要，但实际操作起来却又很模糊。比如，回到上面的高考成绩的例子，我们都认可需要从分数线向上向下选取一定的区间，但是这个区间是多少分呢？换句话说，我们需要选取多大的带宽才能保证分数线上下的人比较相似呢？有的人可能会说1分，另外一个人可能说3分，当然，5分为什么不可以呢？最后，有些人可能觉得10分上下也都没有什么不行的，不会带来系统性的差异。这样的话，带宽的选择变成了一个仁者见仁、智者见智的问题，这种主观性肯定是对我们的分析不利。那么，为了保证我们研究的客观性，我们需要寻找到一些方法，保证我们可以基于经验资料来确定带宽的大小。

目前，回归断点设计中的带宽选择算法有很多。这里不一一列明。仅举两个比较常用的技术。一个是代入法，一个是交互验证法。这两个方法都不是基于我们的经验判断来确定带宽的。先看代入法。这个方法是很简单的。经济学家Imbens和他的同事推导出了一个最优带宽的表达式（Imbens和Kalyanaraman，2012）。基于这个公式，我们只需要将我们研究的具体信息输入进去，带宽自然就确定的。用h来表示带宽，这个公式可以表示如下：

在这个公式中，Ck表示特定的核函数（kernel function）下的常数。c是临界值，（c）是在临界点处使动变量的方差估计值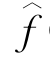，（c）是使动变量在临界点处的分布函数估计。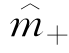（c）表示在临界点以上估计的响应变量和使动变量的关系函数，而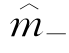（c）表示在临界点以下估计的响应变量和使动变量的关系函数。对于它们分别取二阶导数，我们得到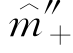（c）和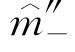（c）。在估计二阶导数的时候，为了提升计算的准确度，需要分别增加一个常数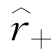和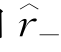。最后，N代表了样本大小。从这个公式可以看出，采用代入法计算带宽需要我们计算一系列的统计量。但实际上，由于目前大家都是采用软件来进行操作，我们并不需要手动计算这些统计量和最后的带宽，很多分析过程都是自动化的了。

另外一个确定带宽的方法叫交互验证法。与带入法相比，交互验证法的逻辑相对复杂一些，其中比较常用的叫留一（leave-one-out）法。

使用这种方法的话，我们首先要做的是先给定一个备选带宽，比如h1。之后，我们从临界点向下，找到距离临界点最近的一个观测值，假定是点A。然后以点A为上边界，再向下h1范围内选取一些观测点。在这个范围内除了点A以外，以其他的点为基础拟合一条回归线。基于这条回归线，预测一下点A处在响应变量Y上的取值，A点的预测值和观测值之间的差值计算出来，假设这个差值的绝对值表示为ΔA。

下一步，我们从A点再向下移动，找到A点之外距离临界点最近的点，假定是点B。针对点B，我们进行同样的操作，将点B作为上边界，向下选取h1范围的点。用范围内B点之外的其他观测点做回归模型，这个模型下B点处Y的预测值和实际观测值之间的差值的绝对值表示为ΔB。

如此这般，将临界线下边的点穷尽，各个点的Δ的值加起来，然后得到一个对应h1带宽的总的Δ值。由于Δ代表了实际值和观测值的差异，可以近似看作一种残差。自然，带宽越好，残差就应该越小。

这时，我们再设定第二个备选带宽h2，然后基于上面同样的分析，得到基于h2的残差值。直到穷尽了各种候选带宽的值。

对于临界点以上，我们采用同样的分析过程，确定最优的带宽。

基于上面的描述，我们可以知道，这样一个带宽选择的过程计算量是很大的。比如，我们可能试了1万个备选h值，如果在临界点左边有1 000个点的话，我们就要针对每一个h值做1 000次回归，一共就做了1千万次回归。当然，手工计算是不可能的，我们都要依靠电脑来进行计算。

讲完了带宽选择问题。我们来介绍一下在作完回归断点设计以后，需要考虑的一系列稳健性检验。

第一个稳健性检验是关于带宽。这部分的分析看的是，如果我们改变带宽选择方法的话，是不是结论就变了。理想的情况，我们改变带宽大小，实质结论不应该变化。那么反过来，如果我们的实质结论只是因为带宽变化就变化了（例如不显著了），那就说明我们的结论是非常不稳健的。这一条稳健估计是很容易理解的。例如，在图7-2中，断点左右各有四个点，如果我们只是将带宽选为临界点左右各两个人的话，会发现两组之间有显著差异。但是如果我们把带宽扩大成左右四人的话，发现临界点左右的均值无差别了。这就说明我们的结论不太稳健。

第二个稳健性检验是在改动临界点的情况下，观察研究结论如何变化。这个检验也称为安慰剂检验，是说如果我们把临界点变动到别的位置，观察结论是否成立。这个检验的原理在于，我们基于观测资料观察到的结论是具有实质意义的，因此如果我们简单地把临界点改变位置，就把我们研究问题的实质意义改变了，那么应该不会存在因果性关系。如果以上大学为例，我们如果把分数线降到200分，那么上大学与否的含义与一开始分数线在600分时定义的上大学与否已经不一样了。此时，我们一开始认为的上大学所具有的因果性关系应该就不一样了。换句话说，我们改变临界点的位置，实质上改变的是自变量的定义，那么定义不同，理应经验模式应该也有所差异。

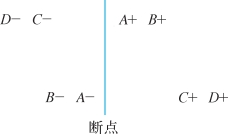
图7-2　结论稳健性示例

第三个稳健性检验关注的是使动变量本身在临界点处是否有显著的差异。上面也说到了，如果说使动变量高考分数在断点处存在跳跃，那就说明有可能有潜在的人为操纵（例如分数线下的人主动通过努力改变成绩以进入分数线以上）或者存在一些我们没有考虑到的混淆因素在起作用。针对这个问题，有专门的检验，叫麦克拉瑞（McCrary）检验。这个检验的原假设是使动变量在临界点处是连续变化的，那么如果麦克拉瑞检验的p值很大，则支持了连续性变化的假设。否则，我们需要认为使动变量在临界点处有比较大的变化。

这里我们展示的是Lee（2008）做得非常经典的在位者优势的例子。所谓的在位者优势，是指在选举过程中，之前已经被选上的“前任”具有优势，很有可能再次当选。这个例子中，处理变量D是之前是否当选，使动变量是上一次选举的时候的得票比例。很显然，如果得票比例超过50%，就会成为在位者（D=1），否则如果上次选举的得票比例低于一半，则不会是在位者（D=0）。响应变量是下次选举是否当选。

在R中，具体的分析过程可以参见https：／／cran.r-project.org／web／packages／rddtools／vignettes／rddtools.html。这里就经验分析简要解释一下。

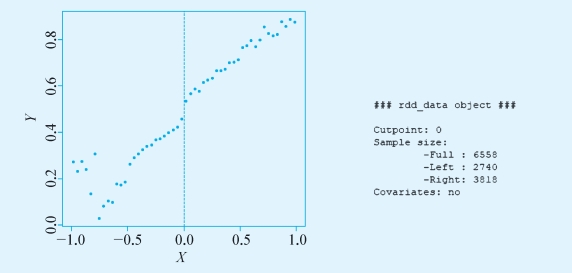
图7-3　R软件输出结果

通过数据描述（图7-3），可以看到在断点处有一个明显的跳跃。在现有数据中，断点左边有2 740人，右边有3 818人。一共样本量是6 558人。这里没有考虑控制变量。

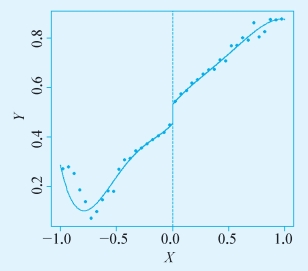
图7-4　R软件输出结果

如果我们分别在断点两边拟合参数模型，就可以估计断点处的因果关系。为了考虑潜在的曲线关系，我们拟合了曲线模型，其中多项式最高为四阶。可以发现，两边模型的截距之差是统计显著的，其代表了因果关系的估计。

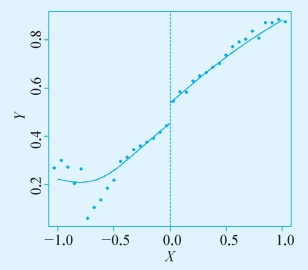
图7-5　R软件输出结果

我们也可以采用非参数方法，使用局部线性回归，并采用代入法来确定带宽。同样，因果关系的估计是统计显著的。

图7-6　R软件输出结果(www.xing528.com)

下面可以看一下使动变量在临界点上下是否连续。图7-6展示，说明基本上可以认为是连续的。通过McCrary检验（p=0.195 2），连续性也得到的支持。

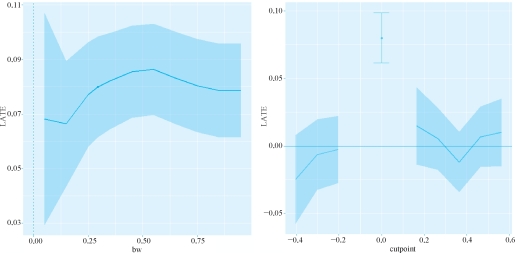
图7-7　R软件输出结果

如果我们更换带宽的话，可以发现结论虽然有一定的波动，但总是成立的。同样，如果我们把临界点换到别的地方，结论就不成立了。因此，这里的回归断点设计是比较稳健的。

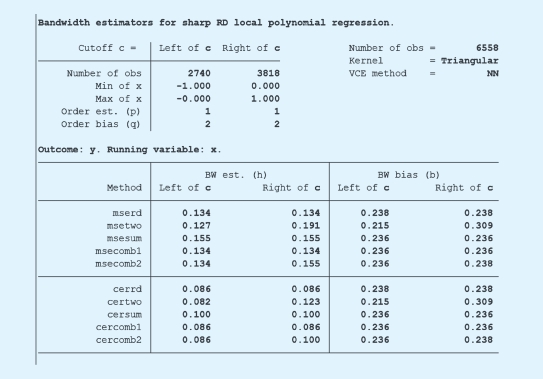
在STATA中，我们可以利用以下代码进行类似的分析。结果和上面的一致，所以不再赘述。对于带宽选择感兴趣的读者，可以使用rdbwselect命令，其中展示了多种新的带宽选择技术。

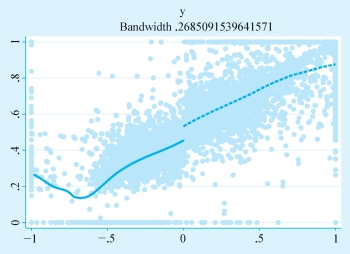
图7-8　STATA软件输出结果

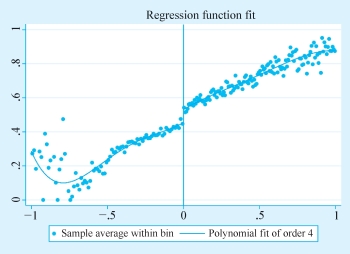
图7-9　STATA软件输出结果

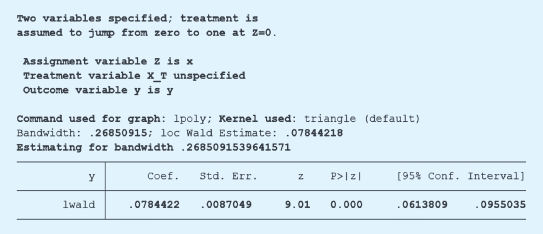
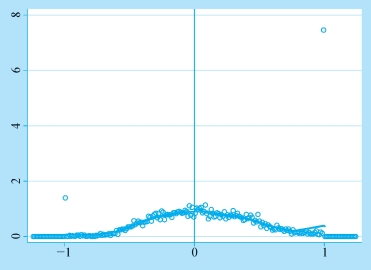
图7-10　STATA软件输出结果

上面例子是确定性的回归断点设计。我们也可以在软件中进行模糊断点设计。虽然在R中，rddtools程序包也可以完成模糊断点设计，但为了展示分析过程，我们也可以采用rdd的程序包。首先我们先用rdd程序包分析上面的例子，采用以下代码：

相关的分析结果如下所示：

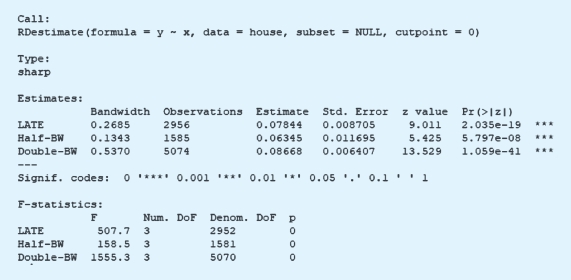
这里我们有三种带宽，LATE模型采用的是Imbens-Kalyanaraman的代入法带宽，另外两个模型分别采用这一带宽的一半以及这一带宽的两倍来作为带宽值。三种带宽下的模型都是显著的（F值），但是估计出的因果效果有一定的差异（Estimate一列的值）。

我们在rdd程序包中也可以作图，如图7-11所示。

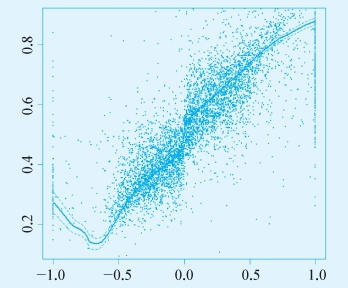
图7-11　R软件输出结果

最后，对使动变量做连续性检验，得到下面的图7-12。

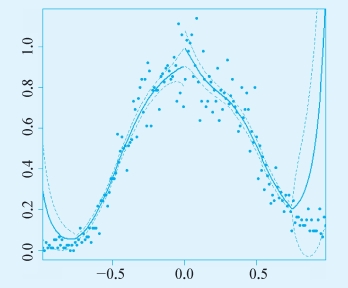
图7-12　R软件输出结果

如果是模糊断点设计的话，我们需要给定处理变量犣。这里，我们在前面的例子的基础上，生成一个处理变量犣。例如，我们可以将犣设定为一个二分变量，在使动变量临界点下面，将犣取值为1的概率设置为0.2。在使动变量临界点上面，将犣取值为1的概率设置为0.8。这样，在使动变量的临界点下面，不是所有人都会落选，个别人的处理变量取值是1（即当选）。而在使动变量临界点上面，也不是所有人都会当选，个别人的处理变量取值是0（即没有当选）。当然，当选的概率从临界点上下来看是逐渐变大的。

利用rdd程序包，我们可以基于下面的代码进行分析：

因果关系的估计系数如下。无论采用什么带宽，都有显著的因果关系。

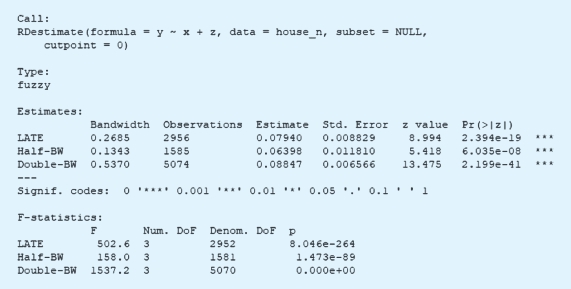
对于模糊断点设计，我们可以作两幅图，一幅针对响应变量在断点处的变化。一幅针对处理变量在断点处的变化。如下所示，二者在断点处都有显著的变化，因此二者的比值构成了模糊回归断点设计的因果效应估计。

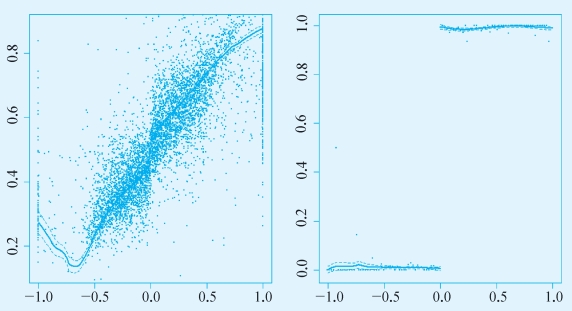
图7-13　R软件输出结果