工具变量方法：探索基本逻辑和因果推论的价值

工具变量的基本逻辑可以用图6-1表示，其中D为自变量，Y为响应变量，U为混淆变量，Z为工具变量。

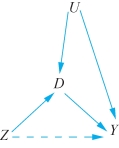
图6-1　工具变量方法原理

很显然，D对Y有影响，这是研究者希望分析的因果关系。但是有一些混淆变量U，一方面影响了D，一方面影响了Y。因为U的存在，D和Y的因果关系没有办法很好地估计出来。这就类似于，是不是上大学D和是不是能赚钱Y这两个变量都和个人的能力U相关，有能力的人一般收入会高一些，有能力的人的教育水平也通常会高一些。但是究竟何为能力，或者什么能力决定了一个人的收入和教育水平，这是很难讲清楚的。自然，如果没有办法控制能力这一混淆变量U，我们估计出的D和Y的关系就有可能是虚假的。例如，我们有可能发现D和Y之间的关系是正向的，看上去好像上大学的人收入比不上大学的人的收入高一些，但有可能上大学的人和能不能挣钱之间不存在什么实质性的关系，只是因为这些读书好的能力也高，而能力高的人挣钱多一些，从而让读书与收入之间才显得是正相关的。如果出现这种情况的话，我们就没办法去准确估算大学教育和收入之间的真正关系。

但是，如果有工具变量Z，研究者就能够探究D和Y之间的真实关联。这个工具变量Z需要和U没有直接关系，也就是图中它们之间没有任何连线。Z和Y也没有“直接”的关系，因此这根线是虚线。但Z可以影响D，D可以影响Y。换句话说，Z对Y的影响必须通过D的传递才能实现。这些便是工具变量的两个基本特征，一来它和混淆变量U没有关系，彼此之间相互独立；二来它和响应变量Y没有直接关系，有任何关系都要通过处理变量去传递。

上面介绍的工具变量的特点可以进一步整合进线性模型中。比如，响应变量Yi可以写成是Di和Ui的函数Yi=β0+β1Di+β2Ui+εi，其中εi是随机扰动项，且和Di、Ui都独立。但是由于测量上的问题，我们没有办法直接观测到Ui，此时Ui就只能进入到随机扰动项中，即随机扰动项变成了β2Ui+εi。自然，如果Ui和Di彼此关联，那么结果便是，因为忽略了Ui，我们所估计的Di的系数时就违背了传统回归模型的假设，所得到的系数β1估计就是有偏差的。

但是，如果我们有工具变量就不一样了。按照上面谈到的，工具变量Zi和Ui是没有关系的。因此，有：

Yi和Zi的关系必须通过Di来传递，所以说通过一个很简单的统计计算，可以发现Yi和Zi的斜方差实际上是Di和Zi的斜方差乘以β1，而β1就是我们感兴趣的Di的系数，具体的计算过程如下：

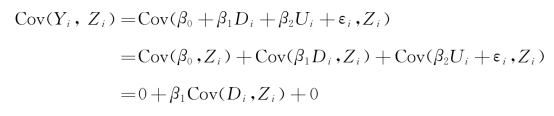
基于这样一种统计关系，估计出β1的取值，就比较容易了，其可以表示为Yi和Zi的协方差比上Di和Zi的协方差。换句话说，我们对于因果关系β的估计就是Yi和Zi的共变程度比上Di和Zi的共变程度，如下所示：

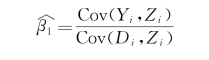(www.xing528.com)

这个看起来似乎很复杂，但还是很容易理解的。这个表达式的分子是Yi和Zi的共变，而Zi并不直接作用于Yi，而是要通过Di来影响Yi。用一个简单的图形来表示，就是：

基于这个图示，Zi对Yi的影响由两部分组成，一部分是Zi如何影响Di（假设用a表示），另一部分则是Di如何影响Yi（假设用b表示）。那么，Zi对Yi的影响就是a×b。如前所述，我们关心的是Di如何影响Yi（也就是b），自然我们用Zi对Yi的影响除以Zi对Di的影响就得到了。换句话说，由于传递性的存在，只要工具变量对Yi的影响算出来了，除以一下工具变量对于自变量Di的影响，就能够得到了自变量对于响应变量的影响，这是一个很直观的想法。

那么在进行因果推论的时候，工具变量会起到什么作用呢？通常而言，工具变量方法和因果推断的交集出现在“样本不服从（non-compliance）”的情况下。什么叫“样本不服从”呢？它描绘的是这样一种情境。比如，医生在进行药物药效分析时，将进入研究的病人分为实验组和控制组。实验组中的病人被要求服药，控制组中的病人被要求不服药。理想的情况是，病人都服从这种安排，按照医生的安排服药或者不服药。但实际会出现什么情况呢？有可能实验组的这些病人中间，一些人偷偷没有服药。同理，控制组的这些病人，有可能通过别的渠道找到这种药吃了。这就是所谓的“样本不服从”。简言之，被研究对象没有服从研究人员的安排，让分析对象吃药，但他或者她不吃，不让分析对象吃药，他或者她偏吃。将样本不服从的情况考虑进来，我们到目前为止讲到的所有关于因果推断的估计量都只能称为意向处理效用（intent-to-treat effect），就是研究者“想要”的那个处理效应。在这个例子中，我们的意向处理效果就是大家在现有安排下的处理效果。但实际情况是，有些人分配到实验组的没吃药，分配到控制组的反而吃药，这就涉及样本不服从情况。

面对这种情况，工具变量便有了用武之地。作为研究者，在一项研究中能做的只能是采用一种随机化的方式来分配处理变量水平（例如随机分发药），但通常没有办法保证我们分发出去的药物，被研究对象一定会按照事前的安排服用或者不服用。此时，我们可以把药物的分发方式看成一个工具变量Z（这里暂时去掉下标i）。由于药物的分配是随机的（比如采用扔硬币的方式决定，扔正面进入实验组被分配到服用药物，扔反面进入到控制组不服用药物），工具变量Z就是一个完全随机的变量，自然和任何潜在的没有观测到的混淆变量U彼此独立。在分药Z到症状Y之间，我们有一个真正关心的处理变量D。D代表了是否吃药。只有通过D，我们才能真正了解药效，所以是否吃药才是我们的处理变量。在这种情况下，我们采用工具变量就能够估计出D对Y的影响。具体而言，药物的分配是随机的，从而构成随机实验。因此，Z对于Y的影响以及Z对于D的影响都能估算出来。这就好比两个随机实验，一个随机实验的响应变量是D，另外一个随机实验的响应变量是Y。换句话说，Z和Y是怎么共变的我们能算出来，同理，Z和D是怎么共变的我们也能算出来。两个一除就得到了D对Y的因果效果。这就是工具变量的好处。就算我们能控制的只是如何分配药品，工具变量方法也能够帮助我们去推算吃药和症状之间的关系。

在社会科学研究中，这种“样本不服从”问题是一个很普遍的问题。比如，我们都知道，北京的车牌是要通过抽签随机分配的。那么，我们可以把它想象成一个随机化的变量。假设我们想知道抽中车牌以后开自己购买的车会不会提升北京居民的幸福感。但是问题在于，很多人即使抽中也可能不会使用车牌（比如没有及时考出驾照）。有些人没抽中，但可以通过别的途径获得车牌从而开上自己的车。我们会发现，在这个研究中，可以保证的只是让被研究对象去抽签，但抽中了以后是不是一定能够享受到那个牌子带来的驾车体验，或者没抽中是不是一定没有办法开自己的车上路，是很难讲的。这里面肯定会有一些“样本不服从”的情况存在，这就要使用工具变量了。与这个例子类似，我们研究教育经历在学龄儿童中的影响时，往往也会利用日期作为工具变量。众所周知，出生在8月后的孩子要晚上学一年的，而对于小孩子而言，这一年会带来体力、智力等各个方面的差异。此时，上学时长的一年差异是我们关心的自变量，而出生日期是我们的工具变量。但是，很多时候，人们的上学安排并不严格遵从规定，一些出生在8月以后的孩子的父母可能采用一些手段让自己的子女早上学，同样一些出生在8月之前的孩子的父母也有可能希望能够推迟子女上学的时间。这也是我们所说的“样本不服从”。此时，出生日期就是工具变量，上学时长是处理变量。

那么，在具体的研究中，应该如何使用工具变量呢？通常而言，我们可以采用二阶段模型法。这个方法是计量经济学中的常规方法，因此这里仅简单介绍一下，感兴趣的读者可以从其他计量经济学教材中获取更多的信息。二阶段模型法拟合两个模型。一个模型以D为响应变量，看什么因素决定了被研究对象是不是吃药。另一个模型以Y为响应变量，看哪些因素决定了被研究对象的症状。如下：

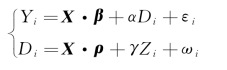
在这个模型中，ωi与Zi和X都彼此独立，εi与Zi和X都彼此独立，但是由于有潜在的混淆因素U存在，εi与Di之间彼此不独立。基于这些设定，可以把Di的表达式代入Y的方程中，得到：

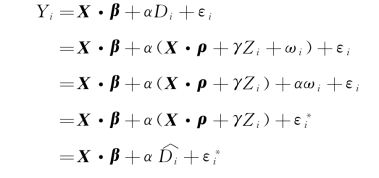
通过上面简单的运算，可以发现，最后的模型相当于把Di的预测值X·ρ+γZi作为一个新的变量放进Yi的模型中，然后去计算它对于Yi的影响，其中的误差项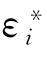=αωi+εi。但是需要注意的是，这里的误差项是有的，因为基于一开始的针对Yi模型，误差项应该是Yi-X·β-αDi，但是当我们把Di的预测值放进去以后，误差项变成了二者并不完全等同。好在目前大多数的软件会自动进行误差的修正，并不需要我们手动计算。此时，我们估计出的α的值就是工具变量对因果关系的估计。