倾向值细分及处理效应异质性的优化方案

最后，所谓的细分，是指将估算出的倾向值得分划分为不同的小的区间。每个区间内部的个体，彼此之间的倾向值差异不大，因此可以近似地看成一个随机实验。那么，我们在每一个区间内去估计因果效果，之后将不同区间的估计综合起来就是总体的平均处理效应的。

关于细分的方法，有必要多说几句。由于倾向值的实质意涵是个体进入实验组的概率，那么当我们对其进行细分的时候，不同组估计出的因果处理效果实际上能够体现出随着进入实验组的概率不同而表现出的处理效应异质性（heterogeneity）。这里可以举一个例子，是布兰德（Jannie Brand）和谢宇关于大学回报异质性的分析（Brand和Xie，2010）。我们都知道，通常而言，上大学的个体的收入平均而言要高于不上大学的个体。但是问题在于，高等教育的回报在不同类型的人中间是不一样的，有些人的回报可能高一些，有些人的回报可能低一些。因此，我们需要分析，同样是大学教育，在不同类型的个体之间的回报有何差异，或者说异质性如何。布兰德和谢宇首先估计出个体上大学的概率，也就是倾向值。之后按照细分的思路，将倾向值从小到大分为几组，在每组内部估计高等教育的回报率。利用图示法表达，如图5-4所示。

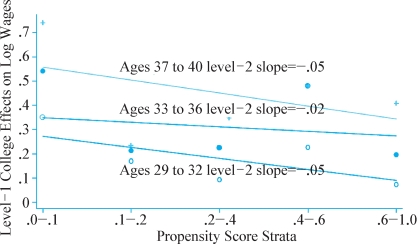
图5-4　处理效应异质性举例

图片来源：Brand and Xie（2010）中的图2（第288页）。

这里X轴是上大学的概率，也就是倾向值，代表了一个人有多大的概率可以上大学。之所以称为strata，是因为这些倾向值被切成了几段，然后在每一段里面估计上大学究竟能给那一段中的个体带来多大的收益。如果每一组的高等教育回报水平用一个点来表示的话，我们就能够用一条回归线来计算这些点所展示出来的基本变化模式，也就是我们所谓的异质性。在这幅图中，可以看到有几条线。这些线是针对不同年龄段的人作的，但它们的趋势是一致的，即全部斜向下。这些模式说明，那些特别不容易上大学的人（倾向值得分比较小的组的人），他们的高等教育回报反而很高。对于那些倾向值数值很高的人而言，他们的回报反而更低。这个模式可以这样理解。假设有两个人，一个人是富二代，一个是穷人的孩子。如果上大学的概率和家庭收入正相关，那么如果让这两个人都去上大学，富二代从大学里面获益不是那么高，反而是穷人的孩子能够从大学的经历里面获益最多。与之相关的一个政策启示便是，大学教育为了社会效益的最大化，应当将录取资格向社会弱势群体（也就是那些不太容易上大学的群体）倾斜。

对于这种分析异质性的研究议题，上面说到的先细分后对各组处理效应进行回归分析的方法也称为细分-多层次法（Stratification-Multilevel Method，SM）。这里之所以说是多层次，是因为我们所拟合的回归模型是基于小组的处理效应估计，因此相比于小组第一层次的细分，回归是更高的第二层次的分析，故而是多层的。除了这一方法之外，我们还可以先将实验组和控制组的个体基于倾向值得分进行匹配，匹配好以后，对于每个匹配对，估算处理效应。之后再看处理效应从倾向值得分低的组到倾向值得分高的组是如何变化的。这里我们可以用一些非参数的平滑方法来看各个匹配对的处理效应是如何变化的。这也称为匹配-平滑法（Matching-Smoothing Method，MS）。与这一思路近似，我们也可以分别对实验组和控制组中的个体的数据先进行平滑处理，看实验组与控制组的人的收入如何随倾向值的变化而变化。之后，将两条平滑变化曲线相减，从而得到处理效应异质性的估计。这个方法被称为平滑-差值法（Smoothing-Differencing Method，SD）。

目前为止，实现这些方法的最简便的软件平台是STATA。假设我们想知道高等教育的回报异质性的话，可以采用以下命令完成上述三种估计方法。

use C：＼Users＼admin＼Desktop＼CGSS10toy12.dta(www.xing528.com)

hte sm lgindiannualincome edu4 female fedu medu fhkagr mhkagr

hte ms lgindiannualincome edu4 female fedu medu fhkagr mhkagr，lpoly（degree（1））

hte sd lgindiannualincome edu4 female fedu medu fhkagr mhkagr，ngrid（100）

分析结果如图5-5。

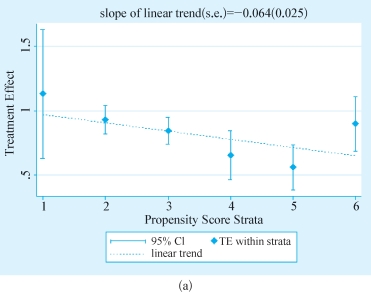
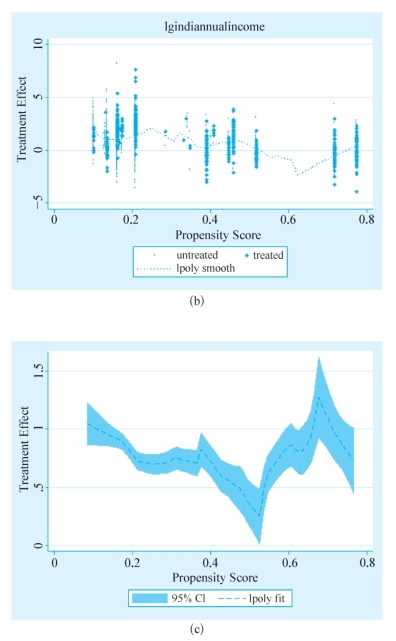
图5-5　STATA软件输出结果

三种结果彼此之间差异比较大，但是SM方法表示出的信息比较具有可解释性，体现出了某种负选择效用。而MS和SD方法则更加精细，可以展示出每一段的倾向值所对应的处理效用大小。