匹配法衡量实验组和控制组匹配质量的方法

关于匹配法，最后需要阐明的问题是在匹配完成以后，如何衡量匹配的质量。对于这个问题，最简单的解决办法就是看一看匹配完成以后，这些混淆变量在实验组和控制组之间的差异是不是变小了。如果匹配完成以后，这些混淆变量在实验组和控制组之间的取值彼此接近。那么我们就能够说，匹配的质量很不错。这里，我们有一个统计量可以具体衡量匹配前后，混淆变量取值在实验组和控制组之间的差异变化。这个称之为标准均值差。

这个公式很清楚，我们看的就是混淆变量在实验组和控制组之间的均值差异，然后除以各自方差加总平均的开根号。需要说明的是，标准化均值差不是T检验，对于T检验的话，如果我们希望比较组a和组b的均值差异，采用下面的公式：

二者的区分还是很明显的，对于T检验，分母部分涉及实验组和控制组的样本量na和nb，而对于标准化均值差，则是除以2。为什么这样操作呢？因为我们的目的是要看实验组、控制组之间的混淆变量是不是在匹配之后变得更加相似，这个相似程度不应该随着样本量的大小而改变。换句话说，实验组和控制组之间在混淆变量上相像与否是一个事实问题，不会因为增加或者减少样本量而改变。像就是像，不像就是不像，做了匹配以后，匹配的质量高低，和样本量的大小应当是无关的。从某种意义上说，样本量大小决定了统计推断的时候的推断质量，而匹配好坏，实际上是一个样本特征。如果匹配得不好，就算是样本量增加了10万倍，实验组还是和控制组之间存在混淆变量的系统差异。正因为如此，在计算标准均值差的时候，不能够把样本信息放进去。

上面针对的是连续型的混淆变量，比照这一公式，对于离散型混淆变量而言，标准化均值差可以写成

除了标准均值差之外，另外一种衡量匹配质量的方法是图式法，这在下面的经验示例中会进一步展示。

最后我们再简要介绍一个使用不多的衡量匹配质量的方法。这个方法看的是实验组和控制组的倾向值分布的重叠度。这个方法实际上是衡量匹配前后，实验组和控制组的倾向值的相像程度。如果匹配后在实验组选取一个人的倾向值，假设这个是0.3。然后看0.3在整个实验组样本中的倾向值分布中的位置。比如果说比0.3数值小的占了全部分布的30%。那么，如果在控制组中，比0.3的倾向值小的占了控制组整体分布的28%。那么，这就说明这两个分布很像。同理，我们也可以看分布的中间的一部分。比如在实验组中，点A和点B之间的面积能够占所有分布的95%。那么，A点和B点所对应的取值挪到控制组的分布上，假设A和B之间的面积也能够占94%或者96%，这也能够说明这两个分布很像，因为它们主要的密度部分重叠了。当然，如果匹配质量很差，那么有可能我们把实验组中的占比95%的AB段挪下来，只占控制组分布的60%。这就说明匹配质量很差，因为在实验组中，倾向值的分布占95%的部分到控制组的分布中只占60%。这说明这两个分布太不一样了，当然匹配的质量就很差。在实验组中占总分布2.5%及以下的取值是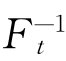（0.025），占总分布97.5%及以下的取值是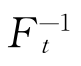（0.975），这样的话，在实验组中占中间95%的AB段如果挪到控制组的话，所占比例πc可以表示为

同理，在实际操作中，我们也可以把控制组的某个AB段挪到实验组去，以衡量两个分布的相似程度，其对应的占比πt为

最后我们简要谈一下匹配后的分析过程。当我们能够做到一个比较好的匹配数据后，最简单的选择是做组间比较（例如T检验）。当然，也可以基于匹配数据做回归模型。这种基于匹配的回归分析也被称为线性回归调整。一些被用于匹配的混淆因素再次在这个回归模型中作为控制变量来使用。线性回归调整的好处在于，可以将可能存在的混淆偏误进行进一步的消减。之所以能够如此，是因为目前为止我们讲的匹配大部分都是非精确匹配。因此匹配过程不可能要求实验组和控制组在混淆因素X上完全一样，自然还会有一些潜在的误差。那么这种误差究竟有多大，我们很难判断。比如，一个60岁的人最后和一个55岁的人匹配起来，差5岁究竟对于Y而言严不严重呢？换句话说，5年的年龄差异究竟会不会带来响应变量Y的巨大变化呢？这个问题很难回答。此时，我们应该将年龄变量依旧在回归模型中控制起来，以尽可能地消减其带来的误差。

在统计软件R和STATA中，我们都可以进行匹配分析。这里我们采用经典的lalonde数据。这个数据中的变量及其含义参见表4-4。其中处理变量为treat（是否参加某培训项目），响应变量为re78（1978年的实际收入），其他为混淆变量。

表4-4　Lolonde数据中的变量及其含义

（续表）

在R里面，我们采用以下命令进行多种匹配。

采用细分法，我们的经验发现如下：

首先针对每一个混淆变量，报告了实验组和控制组各自的均值以及经验quantile函数的差值的最小值、均值和最大值。

由于这里做的是细分，即根据倾向值细分为5个子群，R的输出结果针对每一个子群报告了上述的对比，这里不再赘述。

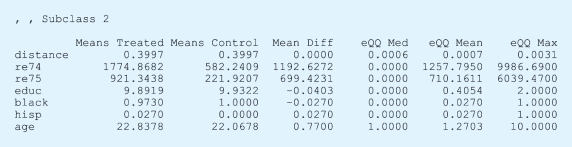
这五个子群的样本量大小如下：

如果将五个子群混淆因素在实验组和控制组之间的差异综合起来，我们有以下结果。

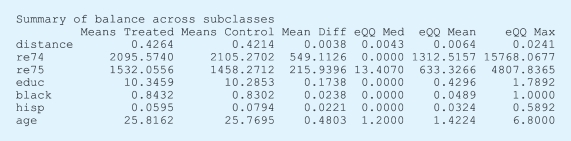
上述结果是根据倾向值细分后剩余的可能的混淆因素不平衡水平，与样本一开始的不平衡情况相比，还是得到了优化，其中优化比例为：(www.xing528.com)

如果采用最近距离匹配，结果会相对简单。如下所示，R的输出结果仅报告了匹配前后混淆因素在实验组和控制组之间的差异情况，以及匹配之后结果的优化情况。需要注意的是，对于re74这个变量而言，最近距离匹配反而拉大了实验组和控制组之间的差异。

最后是遗传匹配的结果。同样，只是报告了匹配前后混淆变量平衡水平及其可能的优化。

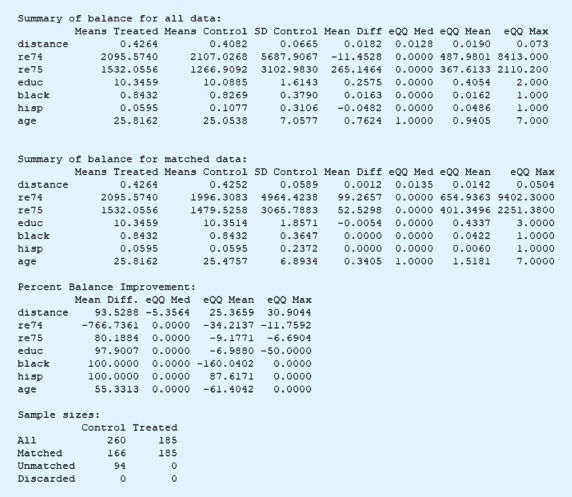
之后，检验一下混淆变量在匹配前后的平衡性变化。通过love.plot命令，我们可以发现，采用遗传匹配，除了re74之外，其他混淆变量在实验组和控制组之间的平衡性都得到了优化。

我们也可以查看Jitter图。可以发现，匹配后实验组中的样本与控制组中的样本有很大一部分是重叠的。当然，一部分的控制组中的样本因为缺少匹配对象而被删除掉了。

如果看匹配前后倾向值的分布情况，我们可以发现，整体而言，倾向值在实验组与控制组之间的匹配得到了提升。

图4-6　绝对均值差异

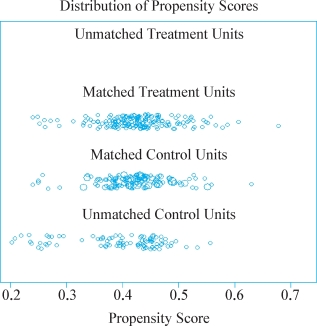
图4-7　倾向值重叠度

图4-8　倾向值分布对比

最后，在得到匹配样本之后，我们可以基于匹配样本拟合回归模型，相关结果如下，其系数的解释与常规回归方法一致，这里不再赘述。

与R相比，STATA中对于匹配方法的操作是围绕着直接估计因果关系的系数展开的。具体我们使用的命令如下所示。

各种匹配结果如下所示。

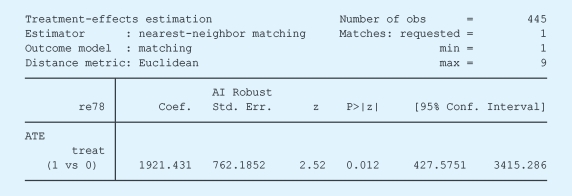
在实验组和控制组之间，倾向值的重叠程度可以用图4-9表示。

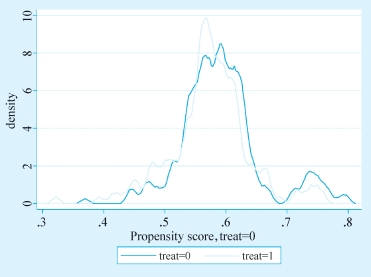
图4-9　倾向值的重叠程度

针对混淆变量age，我们可以检查其匹配前后的平衡性变化，如图4-10和图4-11所示。

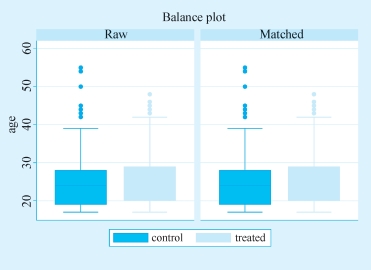
图4-10　混淆变量age匹配前后的平衡性变化

图4-11　变量Density匹配前后的平衡性变化

整体的对于所有混淆因素的平衡性分析结果如下所示。