匹配法操作过程中的平衡问题及样本量的控制

关于匹配的具体步骤，我们可以进行两种基本的区分。一种匹配叫精确匹配，另一种匹配叫非精确匹配。什么叫精确匹配呢？很简单，就是说找来的和某个个体匹配的对象，和这个个体的混淆特征的取值要一模一样。比如，一个研究中的一个研究对象性别是男性，城市户籍，重点高中毕业。那么为了找到与之精确匹配的对象，也需要找一个男性、城市户籍、重点高中毕业的人。很明显，精确匹配是最好的状态，因为通过精确匹配，一项研究保证了在所有能观测到的混淆变量上，被匹配的两个人之间绝对是一样的，也就是说，在所有混淆因素上都是取值一样的，所以说这是一个最好的匹配策略。

但是很遗憾，精确匹配在现实中使用得很少。原因在于，精确匹配是“样本杀手”。比如，一项研究一开始有1万个样本，如果一定要坚持精确匹配的话，有可能最后只剩下二三十个人了。这是因为精确匹配的过程匹配的不是一个混淆变量，而是很多混淆变量。而且有一些混淆因素是连续性变量。那么精确匹配对于匹配对象的要求就非常高。比如年龄，找一个老年人匹配一个老年人相对容易，但一定要找一个60岁的人匹配另一个60岁的人，对匹配对象的选择就会有太大的限制，自然不是那么容易找得到。如果样本足够大，当然可能找得到这种对象，但是大部分其他人就是不符合这个条件的了。那么，如果研究者一定要坚持精确匹配，最终的匹配样本就会变得非常小。从某种意义上说，这里涉及的是匹配法过程中的平衡问题。如果研究者想要大样本，那么匹配的过程就不能那么精确。如果研究者想要一个精确的匹配，那么最后剩下的匹配样本就不可能那么大。正是在这个意义上，很多时候社会科学研究者需要有一定的样本量来保证统计检定力，故而采用的是非精确匹配方法。

所谓非精确匹配，是说一项研究中，要求的匹配关系不一定在混淆因素上取值一模一样，只是近似即可。比如被研究对象是一个60岁的人，找一个59岁的人和他匹配也差不多。这样做之所以可行，是因为我们通常觉得即使有误差，也不会有太大的问题，只不过差了1岁而已。那么，61岁的人可否用来和60岁的人匹配呢？也可以。62岁的人呢？似乎也没有太大问题。按照这种近似而非严格一致的原则进行的匹配就是非精确匹配。基于上文的讨论，这种非精确匹配是尽量在匹配的精度和样本量之间寻求一种平衡。我们在放宽匹配精度的情况下，尽量保证样本量。这对于大多数社会科学研究者而言是比较现实的一种方法。因此，大多数的研究使用匹配方法的时候采用的是非精确匹配的手段。

当然，无论是精确匹配还是非精确匹配，都需要找到一些指标来衡量不同个体在混淆因素上的距离。从本质上讲，我们认为个体A和个体B能够匹配起来，就是因为他们在混淆因素上距离更近。假设只有实验组和控制组两组人，我们可以从实验组出发，针对实验组中的个体I，收集其一系列背景信息X（例如性别、年龄、教育水平等）。之后，我们转到控制组中的个体。假设控制组有三个人，分别是A、B和C，这时候我分别计算A和I，B和I，以及C和I在X上的距离。然后将与I距离最近的一个控制组个体挑选出来与I匹配起来。

但是，距离的测量并不是一件简单的事情。在实际操作过程中，研究者有很多的选择。最简单的一种匹配就是精确匹配。精确匹配很简单，如果实验组的个体I和控制组的个体J在混淆变量X上的取值是一样的，我们就认为他们的距离是0。换句话说，在混淆变量构成的一个空间或者超空间上，I和J重叠了。但是，依据精确匹配，只要他们的X取值不一样，那么我们就认为他们的距离是无穷大的。换句话说，只要在一个方面不严格一样，距离就要设定为无穷大，因此不能匹配起来。唯有在混淆变量X上完全一样，才匹配起来。如果我们用Dij来指代个体i和个体j之间的距离，精确匹配可以表示为

除了精确匹配之外，现实中用的比较多的距离测量叫马哈拉诺比斯（Mahalanobis）距离。马哈拉诺比斯是一个印度统计学家的名字。从某种意义上说，马哈拉诺比斯距离是对常规的欧几里得距离（又称欧氏距离）的扩展。比如，在二维空间里面计算两个点的距离。这两个点它们都有各自的坐标，那么欧几里得距离就是坐标差的平方和，然后开根号：

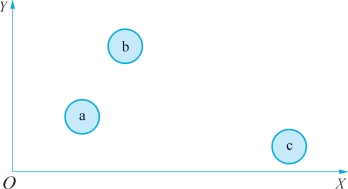
图4-1　欧氏距离举例

例如，如果我们的匹配是在图中这个二维空间里去做的话，a代表实验组中的个体，b和c代表控制组中的个体。很明显，那肯定是a和b匹配起来，因为它们的欧氏距离更近。这里的例子只是一个二维空间，如果实际研究中有超过两个维度的信息，可以把二维扩到三维、四维等。在三维空间中的话，欧氏距离的计算公式只需要再加上第三个维度上坐标差值的平方即可，例如。也就是说，维度可以不断地扩展，但基本的计算方法是一样的。

但是，欧氏距离的问题在于，我们的计算过程没有把X和Y变化的量纲差异考虑进去。在上面的例子中，我们说欧氏距离可以使用，一个前提是，横轴变动的单位和纵轴变动的单位一样。比如在我们都很熟悉的欧氏坐标系中，横轴变动1，纵轴变动1，这个变动的量纲或者单位是一样的，代表着同样水平的变动，参照标准是一样的。但问题是，很多时候两个轴的数字变动的参照系并不一样。比如，我们对比两个人跑动的距离，一个人跑的距离是10 m，另一个人跑的是5 m，我们一般会说10 m肯定比5 m长。但这个说法是不严谨的，因为我们不知道这两个人所参照的对象是什么。比如，在一些最多只能跑5 m的人中间，一个人跑了4 m，已经可以算得上是很长的一段距离了。但是如果在一些随意就能够跑100 m的人中间，某个人只能跑10 m，这个距离实际上是很短的。所以，当两个人去对比的时候，究竟谁可以称得上跑的距离“长”，还需要结合他们各自的参照对象来考虑。也就是说，参照系有一个各自的参照标准，我们以此为依据判断个体之间的高下比较合理。将参照系考虑到距离的测量中便是马哈拉诺比斯距离所完成的工作。如果我们在一维的情况下看，马哈拉诺比斯距离的公式可以表示如下：

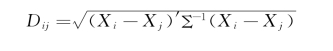
和欧氏距离相比，马哈拉诺比斯距离增加了对X协方差Σ的考虑，即乘以协方差矩阵的逆矩阵。这个公式看起来似乎很复杂，但实际上非常容易理解。从本质上看，马哈拉诺比斯距离就是标准化以后的欧几里得距离。所谓标准化，就是计算一下标准得分。相信读者们对于标准分都不陌生。在高考的时候，不同省份之间的考生进行比较都需要基于标准分而非原始分。通过除以衡量变动程度的一个统计量（标准差），一个在北京参加高考的考生的成绩，就转变成了所有北京考生考分的变异程度下该考生的名次。这种相对名次在不同省份之间就是彼此可比的了。马哈拉诺比斯距离所计算的距离就是把这种可比性考虑进去，从而在尺度上进行统一。从这个角度来说，马哈拉诺比斯距离通常要比欧几里得距离使用的范围更广（如果变化量纲一致，则Σ为单位矩阵，马氏距离就变成了欧氏距离）。

在具体的研究项目中，研究者有可能需要计算欧氏距离或者马氏距离，这里我们展示一下在R里面如何进行具体的操作。这里采用很经典的鸢尾花数据，我们只选用其中四个变量的六个观测值使用，数据如下：

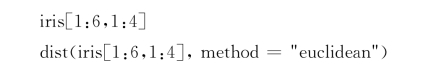
这个数据是衡量鸢尾花的不同特征。例如，sepal.length和sepal.width是指萼片的长度和宽度，petal.length和petal.width是指花瓣的长度和宽度。

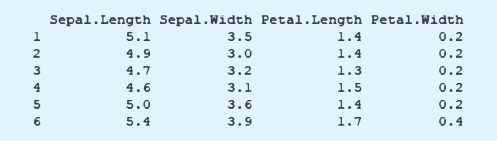
欧氏距离的计算，我们采用了dist命令，得到的分析结果如下：

在生成的距离矩阵中，可以看到，第一行观测和第二行观测之间的欧氏距离为0.538，其他数值的解释同理。

为了计算马氏距离，我们使用Stat Match包，其中的mahalanobis.dist命令可以帮助我们计算马氏距离，如下：

和欧氏距离不同，第一行和第二行观测之间的马氏距离值为2.237。

上面的计算采用的是封装好的统计包。实际上，无论是欧氏距离还是马氏距离，手动计算也都比较简单。例如，数据中第一行和第二行观测点的欧氏距离的计算方式如下：

在计算马氏距离的时候，我们首先需要知道这四个变量两两之间的协方差信息，如果用A来表示协方差矩阵，我们有：

那么，第一行和第二行观测在这四个变量上的算术差值设为V，基于A和V的值，我们计算第一行和第二行观测之间的马氏距离，得到2.237。这部分计算的代码如下：

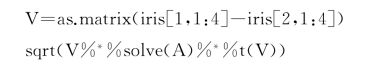
除了欧氏距离和马氏距离之外，第三个衡量距离的方法是基于倾向值。如上文所讲到的，所谓倾向值，是指个体进入实验组（相对于控制组而言）的概率（这里用e表示）。由于在观测性研究中，这个倾向值是基于混淆变量估计出来的，因此我们就可以用不同个体之间估计出的倾向值大小来衡量二者之间的距离，如下：

我们之所以能够用倾向值来衡量个体的距离，是因为倾向值是所有混淆变量的一个总结性变量。从本质上讲，当两个被研究对象在混淆变量上不一样的时候，这种差异之所以重要，不是因为这种差异本身重要，而是因为由于这种差异，这两个个体接受处理变量影响的概率不一样了。比如，一个被研究对象是男的，另一个被研究对象是女的，这种性别差异对于一项研究而言是需要处理的，原因在于由于性别不同，上大学的概率不一样，从而进一步干扰到分析上大学的经济回报问题。同样的理由，年龄不同和户籍不同等混淆因素上的差异性，最终都体现在人们进入实验组和控制组的概率差异上，这个概率差异就是倾向值的距离。正因为如此，我们可以基于这些混淆变量计算出的倾向值的得分，进一步算一下它们的差值以衡量个体间的距离。

实际上，基于倾向值的分析让计算过程变得更简单了。这是因为倾向值本身就是一个数值，是一维的。因此，我们只需要用一个个体的倾向值得分减掉另一个个体的倾向值得分即可，这个分析过程和马氏距离的计算相比，明显简化很多，毕竟用个体A的一串特征和个体B的一串特征进行匹配，工作量是很大的。尤其是如果处理变量的类别超过两个，工作量会迅速增长。在此情况下，倾向值匹配的优势就很明显了。

基于倾向值去进行匹配也有一个问题，即倾向值的取值范围是在0～1。所以，两个个体的倾向值的差值的取值范围就很窄（-1～1）。而由于这种比较窄的变动范围，我们匹配过程就不得不患得患失，因而不利于最终的匹配。比如，10和10.1这两个数值匹配起来好像没有问题，但是，0.1和0.2能匹配吗？我们似乎感觉没有那么自信，是因为其差值相比于原本的取值也算比较大的了。虽然两个的差值都是0.1，但由于一开始的数值起点也小，后续的匹配就有可能不是特别好。

为了解决这个问题，我们就需要把0～1变动的倾向值想办法转换成一个从负无穷大到正无穷大变化的一个值。数学上，这可以通过logit变换完成。所谓logit变换，就是做如下操作：

通过这种变换，一个取值在0～1的数值e就转换成了一个取值范围从负无穷大到正无穷大的一个值了。此时，如果我们的匹配基于logit变换后的倾向值，两个被研究对象之间的差值也是负无穷大到正无穷大。由于距离不能够为负值，所以最后它们的距离从0到正无穷大，此时距离的定义如下：

这种匹配也叫线性倾向值匹配。由于线性倾向值的取值范围较之之前的原始倾向值得分更加宽，这种取值范围更加有助于我们做匹配。这里需要说明的是，究竟倾向值差异或者线性倾向值差异多大才能够算接近，标准通常是由研究者来定的。比如，我们可以对距离差异没有任何容忍度，这就是一个精确匹配的过程。对于一个倾向值是0.69的人，我们一定要找一个0.69的人与之匹配。但是，如果我们对于距离的容忍是在正负0.1之间，那么，倾向值为0.69的人就可以和倾向值为0.68～0.70的任何一个人匹配。如果我们对于距离的容忍度是0.05，那么和倾向值为0.69的个体进行匹配的人就是那些倾向值在0.64～0.74的分析对象。当然，能不能找到合适的人来进行匹配，也取决于数据质量，即数据中是否有比较相似的对象。

上述的这些测量距离的方法可以有一个综合的运用。比如，一项研究中，研究人员可以先看一看两个个体之间的线性倾向值究竟差多少？如果差得很多，就没有必要进行下一步的匹配，毕竟这两个人之间的距离已经很大了。此时，我们可以认为这两个人之间的距离无穷大。实际操作中，我们可以给这个无穷大的距离一个具体的数值，比如将距离值设定为9 999。面对这么大的数值，基本上没有软件会去将两个人匹配起来。另一方面，如果线性倾向值的差距是在可接受范围内，这就说明个体之间的倾向值没有差别那么大。在此情况下，我们可再进一步使用马哈拉诺比斯匹配或者精确匹配。上述的操作可以用公式表示：如果|logit（ei）-logit（ej）|≤c，则Dij=否则Dij=∞

这就是对上面多个距离测量的综合运用，把线性倾向值匹配和马哈拉诺比斯距离匹配两个结合在一起。其中，线性倾向值的距离是一个限定条件，后续的马哈拉诺比斯距离用来进行实际的匹配操作。

在确定了距离的度量之后，下一步要做的就是具体进行匹配了。这里要解决三个问题：（1）每个个体能够匹配几个对象；（2）在匹配的过程中，每个个体是否能够重复使用；（3）匹配的算法。对于这三个问题，我们分别讨论。

1.匹配对象个数

我们首先看第一个问题，即匹配对象的数量。对于这个问题，我们基本上有两种匹配方法，一种叫一对一匹配，一种叫一对多匹配。一对一匹配，就是说一个实验组的人匹配一个控制组的人，反之亦然；一对多的话，一个实验组的个体要匹配多个控制组的对象，或者一个控制组的个体匹配多个实验组的人。一对一匹配有什么好处呢？经过一对一匹配，匹配的误差会很小，因为每次在做匹配的时候，都是找了一个和某个对象最相似的人去匹配，所以说这时候匹配的两个人之间的差异是很小的。但是，通过一对一匹配的话，后续分析的方差会很大。这是因为最终的样本量会被压缩，每一个匹配对也就是两个人而已。与一对一匹配相比，如果一项研究允许一对多匹配的话，这时候最终的样本会很大，所以方差会相对而言更小。但是，一旦允许一对多匹配，就意味着一个被分析对象和他或者她“最”接近的那个人匹配起来了，同时又跟与其“次”接近的人也匹配起来了。自然，匹配的质量就会受到影响，整体的误差就会升高。(www.xing528.com)

实际上，上面谈到的一对一或者一对多的匹配，展现的就是经典的方差与误差的平衡关系。误差变大了，样本也变大了，方差就变小了。因此，具体采用什么方法是研究者的一个选择。通常来讲，在实际操作中用的最多的还是一对一匹配，一对多的匹配用的不是特别多。

需要说明的是，一对多匹配过程中，匹配对象的个数可以是不固定的。例如，一对N的匹配过程，这个N是可以变动，对于不同的个体来讲不一样。比如，一号被研究对象进行一对二匹配，二号被研究对象可以进行一对一匹配，三号被研究对象可以进行一对三匹配，这实际上是可变动的匹配。虽然这种匹配引入了某种灵活性，但是我们需要在后续的分析过程中进行加权。这是因为，不同的匹配对的大小不一样了。如果一对一匹配的话，每一对都是两个人，这时候各个匹配对的权重都是一样的。但如果允许一对多匹配的话，有的匹配对就两个人，有的匹配对是四个人，有的匹配对是三个人，这时候我们不得不需要特定的加权方案对他们进行处理。

讲到这里，我们需要讨论一下匹配过程的样本损失问题。无论采用什么距离测量，我们在匹配之后的匹配样本与原始样本相比，肯定是有样本损失的。基于特定的研究问题，有时候一个6 000多个样本的数据，匹配下来只能剩下200多个人了。当然，也有最极端的情况，匹配以后的匹配样本和原来的样本差不多大，没有样本损失，但这是很少见的。通常而言，一个很大的样本匹配完之后，留下来的分析对象有可能只是原来样本的二分之一甚至五分之一大。

但是，这种样本损失对于分析的统计检定力而言，影响不会特别大。理由有两个。第一，统计的检定力取决于实验组、控制组哪一个更小。通常而言，正如前文所言，很多研究最终关心的是ATT，即针对实验组的平均处理效应。这时候，最好的情况是实验组比较小，而控制组相对而言更大。我们就有足够的控制组候选人来匹配实验组中的个体。最理想的情况，我们能够保证实验组的每个人都能有控制组中的人与之匹配起来。也就是说，控制组要足够大，以提供足够多的备选对象跟实验组的人去配对。因此，样本检定力主要取决于实验组和控制组中相对更小的那一组的容量。第二，通过匹配，可以提升样本相似度，从而降低了因为模型不确定性带来的误差，进而提升统计检定力。这一点可以从那些没有能够和实验组的人进行匹配的控制组个体这个角度来看。通常而言，匹配完了以后，把没有能够进行匹配的个体删掉。这个过程实际上是在尽可能保留有用的信息，而删除冗余信息，从而提升数据质量。这是因为删掉的人没有办法找到和他们匹配的人。换句话说，他们太独特，以至于找不到和他们相似的人。回到前文谈到的因果推论的假设，对于这些人，我们实际上没有办法去探究他们的反事实的状态。从倾向值的估计角度来说，因为我们在现有的资料中找不到和这些特殊对象特别像的人，这些人的倾向值就会特别极端。如果是控制组的个体，有可能他们的倾向值低到非常接近0，对于他们而言，正值假设就会受到质疑。因此，匹配只不过是把多余的信息删掉，同时把最后有用的可以进行反事实因果推断的样本保留下来。故而匹配之后对于统计检定力的影响应该不大。实际上，如果把这些极端的个体留在分析样本中，数据中实验组和控制组之间的可比性就会被拉低。此时，研究者的模型或者拟合不出来，或者即使拟合出来，也会用到很多模型外推的手段，这当然不是一个很好的情况。

2.匹配对象重复使用

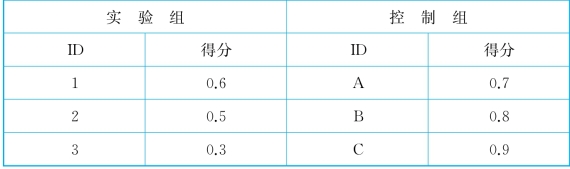
关于匹配方法的另一个重要问题是，一个被研究对象能不能使用很多次。假设实验组中的三个人编号为1、2、3，控制组中的三个人编号为A、B、C。如果1号和A匹配了，2号和B匹配了，那么3号是否还能够再和A或者B匹配呢？如果可以的话，那么这就涉及被研究对象的重复使用了。如果不允许重复使用，一旦某个个体被匹配完了以后，这个个体就被拿走，再也不会在后续的匹配过程中考虑进来。这样一种匹配方法也称为贪婪匹配。这是因为这种匹配的逻辑是先到先得，把和自己最像的人匹配好而不考虑其他人了。之后，这个被匹配的对象就被拿掉，后面来的人不可能与之匹配。在上面谈到的例子中，实验组中的1号首先进行匹配，查看了控制组中的三个人，发现A和自己最像。于是1-A匹配。然后，2号来了，但是，已经没有A作为候选了，2只能去看B和C谁和自己最相像。如果2号发现C和自己很像，那么就和C匹配。此时，3号最后一个来，就没有选择，只剩下B，也就只能和B匹配了。对于贪婪匹配，很重要的因素是谁先匹配，先挑选的那个对象肯定匹配质量是最高的。同时，后挑选的对象有可能匹配质量很差。还是回到这个例子。假设我们用一个数字来衡量个体的特征（这个数字可以理解为倾向值，如表4-1所示），1号、2号和3号三个人的数值分别是0.6、0.5、0.3，A、B和C这边的数值分别是0.7、0.8和0.9，这时候1号的0.6的分数会和得分为0.7的A进行匹配。2号基于自己0.5的分值，在剩下B的0.8和C的0.9中间，只能选B的0.8了。选完以后，C的0.9只能够和3号的0.3进行匹配。很显然，C和3号的取值差异已经很大了。

表4-1　匹配举例Ⅰ

但是，如果研究者允许一个个体能够反复使用，那么挑选的顺序就不重要了。相应地，匹配的质量也会得到提高。之所以匹配质量会提高，是因为每个个体都能够找和自己最接近的个体去匹配，而这个最接近的个体有可能同时和很多人都很像。在重复使用的情况下，回到上面的例子中，1、2、3都和A去匹配，A就用了三次。这样的匹配情况下，整个匹配质量是可以提高。

但是重复使用也有自己的问题。即每个匹配对彼此之间不是独立的。比如，1和A匹配，2和A匹配，1-A和2-A这两对人就不是彼此独立的，因为他们有一个共同的个体A，这对于后续的统计处理而言是挺麻烦的一个事情，毕竟几乎所有的统计分析的假设前提是不同对数之间彼此独立。除此之外，还有一个麻烦的问题是，如果一个个体被反复的使用的话，一种最极端的情况是这里所展示的，A和所有的实验组的人都很像，结果发现1、2和3号都和A匹配起来，对A反复的使用，实际上造成的结果是，控制组的其他人（B和C）就没用了。换句话说，控制组的信息就变得非常的同质化，因为对于这个匹配过程而言，控制组就一个人A（被使用很多次），而B、C都是被视为冗余的了。

3.匹配算法

下面一个要讨论的问题是怎么进行匹配。基于上面的讨论，个体间的距离计算出来了，同时研究者也决定好了是采用一对一还是一对多匹配，以及可不可以个体重复使用，下面就是实际操作进行匹配了。具体的匹配过程可以采用的策略有很多。上面谈到贪婪匹配就是其中之一。找到和自己最接近的人然后匹配起来，这是一个非常直来直去的匹配方法。除了这种方法以外，还有一种方法叫最优匹配，它“优”在哪里呢？对于最优匹配而言，这时候需要考虑的因素已经不再是单个个体的匹配优度，而是整体的匹配优度。这是最优匹配的一个最基本的特征。换句话说，最优匹配的方法优化的是整体的状态，而不是单个个体的状态。换个角度来说，在贪婪匹配中，我们的思路是要保证每次匹配的时候被匹配的对象之间的距离最小。比如说1号，找一个和自己最相像的，2找一个和自己最相像的，以此类推。研究者寻求的是每次匹配时个体层次上的匹配达到最优（即距离最短）。但是这里所说的最优匹配，看的是整体的“平均”距离。这里可以展示一个具体的例子。

在表4-2中，如果采用贪婪匹配的话，一个匹配的方式是A匹配V，B匹配Z，C匹配X，D匹配Y。这些匹配对的平均距离是3.6。但如果采用最优匹配的话，看的是整体最优，一个匹配策略的就是AV、BX、C-Y和DZ，这时候整体的平均距离就变成了3.4。实际上，所谓的最优匹配，我们是很熟悉的。从某种角度来说，这就相当于田忌赛马，每一轮比赛的时候拿自己最厉害的马和对方最厉害的马去比赛，这时三轮比赛有可能全部输掉。但是田忌放掉一轮，把最差的马和对方最好的马去比赛，但是后面两轮都能赢，这时候就能达到整体最优。可见，如果研究的目的只是看到单轮最优的话，那最后可能全盘达不到最优的状态。而把目标放在整体最优上，“成本”只是某些个别匹配达不到最优而已。

表4-2　匹配举例Ⅱ

需要提及的是，在最优匹配里面有一种匹配方法叫全匹配（full matching）。在这种匹配策略下，研究者不再是关注每两个个体的匹配，而是把所有人看成一整块，然后像切蛋糕一样，尽量保证切的每块蛋糕内部，匹配对象的整体距离最小。这时候有可能在某块蛋糕内一个实验组的人匹配两个控制组的人，而在另外一块蛋糕中，一个实验组的人只匹配一个控制组的人。在全匹配中，我们不再纠缠于究竟是一对多还是多对一，最终的目的就是保证每一块内部，至少每个实验组的人都能找到相应的匹配对象。而为了达成这一目标，我们就是把整个空间做了一个分割，这就是所谓的全匹配。一个全匹配的过程可以通过图4-2展示。其中，不同的色块代表了切出来的不同的蛋糕“块”。我们需要做的是，保证在每个色块中，至少有一个实验组的人和至少有一个控制组的人。在日常实践中，全匹配是比较常见的一个最优匹配的方法。

图4-2　全匹配示例

总结一下，最优匹配有以下三个优点。第一个优点，和一般的贪婪匹配相比，最优匹配不存在顺序效应。也就是说，采取最优匹配的话，不存在先到先得的问题。第二个优点，至少能够保证所有实验组的人都能在控制组中找到匹配对象。在传统的匹配策略中，很有可能一些实验组的人因为难以寻找到控制组的匹配对象而被放弃掉。第三个优点，考虑到全匹配的优势，采用最优匹配的话，可以使用全匹配的策略，而传统的匹配过程无法使用全匹配。

除了最优匹配，还有一种匹配方法就是直接拿倾向值得分去匹配。倾向值最大的优点就是它可以降维。如上文所述，一开始的时候研究者可能面对很多混淆变量。这些混淆变量的数量如此之多，以至于直接进行匹配的话计算难度比较大。但是如果把它们都“总结”为一个倾向值得分的话，后续需要做的只是基于倾向值进行匹配即可。这是倾向值匹配的一个非常突出的优势，即只是在一维水平进行匹配，而不是在多维上进行匹配。在一维上进行匹配非常容易，如果把这个倾向值进行了线性处理（例如进行logit变换）的话，其取值能从负无穷大到正无穷大，这时候把所有个体的倾向值进行排序，然后就近匹配即可。也就是说，这相当于在一把尺子上找最近的点去匹配，从而把很复杂的多维情况变成了一个一维的匹配。

此外，采用倾向值进行匹配的话，研究者也可以选定一个范围进行匹配，这个叫卡尺（caliper）匹配。所谓的卡尺，实际上就是一个半径范围。比如说研究者可以将卡尺定在0.1。那么对于一个倾向值取值是0.3的实验组个体而言，在控制组中倾向值在0.2～0.4的所有人都可以拿来和这个倾向值为0.3的实验组个体进行匹配。只是，卡尺的具体值需要研究者自己来设定。这里提醒一点，这个卡尺半径不能设置得太小，设置太小，实际上和精确匹配没有区别。比如说对于倾向值为0.3的个体，研究者将卡尺半径设定为0.000 01，就没有太大的意义了。通常来说，比较常见的卡尺半径值是0.01或者0.05。卡尺匹配可以用图4-3表示。

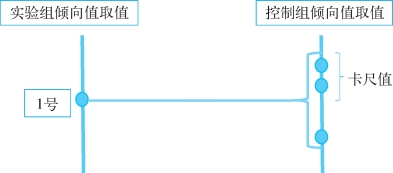
图4-3　卡尺匹配示例

还有一种匹配方法在经济学里面用得比较多，称为核函数（kernel function）匹配。前面介绍过，传统的匹配方法，是针对特定实验组中的某个对象，挑一个或者几个和他或者她特别像的人匹配起来，但是一些无法找到匹配对象的人会被删除掉，这有可能造成样本的严重损失。与之相比，核函数匹配尽可能地保留原始数据。比如，还是用表4-3描述的情形为例。

表4-3　匹配举例Ⅲ

实验组中的个体1的倾向值得分为0.6，而在控制组中，和他最像的人是个体B。在传统的贪婪匹配中，1-B匹配即可。但是对于核函数匹配来说，则是定义一个权重设定。比如，在这里对于控制组中的A、B、C各自设定了一个权重，由于B和1最接近，我们可以给B很大的权重。而取值为0.5的个体A和1号之间的距离稍微远了一点，我们可以给他次大的权重。最后，C的0.9的取值和1号的0.6的取值相比，距离是最远的，那我们给他一个最小的权重。这时候，我们需要把A、B、C三者的值做一个加权平均，然后用这个加权平均的数值和个体1进行匹配。如果A、B和C的权重分别是W1、W2和W3的话，那么，和1号进行匹配的数值不再是某一个单个个体的观测值，而是他们数值的加权平均，即W1×0.5+W2×0.63+W3×0.9，其中W1+W2+W3=1。

可见，核函数匹配的好处就在于每个被研究对象都会被用上，此时，最后使用的匹配样本就会因为有充足的样本量来保证统计效率。除此之外，核函数匹配还有一个好处。即对于W1、W2、W3这些权重的基本状态，有一些已经形成的比较成熟的权重描述。这是什么意思呢？我们都知道，在安排权重的时候，需要对最相像的个体给予一个很大的权重，而随着距离越远，权重越低。但是从高权重到低权重的赋值变化过程可以有很多模式。比如，随着距离的越来越远，权重可以有一个线性下降，也可以有一个曲线下降。这些不同权重下降的方式分别对应了不同的核函数。例如，权重的分布可以是正态分布，从中心点（最相像的人）向两侧平滑下降。最后需要特别说明的是，核函数匹配可以囊括上面讲到的卡尺匹配。具体操作上，只需要采用均匀分布核函数即可。基于这一核函数，与被研究对象最相像的人左右两侧一定范围内的个体赋予同样的权重，相当于在一定的范围内计算平均值，而超出这个范围的个体权重为0，即不予考虑。这些方法可以用图4-4和图4-5表示，其中我们关心的是实验组的1号的匹配。

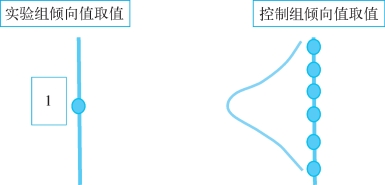
图4-4　正态分布核函数示例

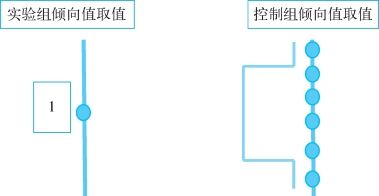
图4-5　均匀分布核函数示例

最后一个匹配方法，叫遗传匹配（genetic matching）。遗传匹配可以看成倾向值匹配与马哈拉诺比斯距离匹配的一个综合。回到之前讲到的马哈拉诺比斯距离，它的表达式如下：

而在遗传匹配中，个体间的距离计算是

与马哈拉诺比斯距离相比，遗传匹配所采用的距离度量增加了一个权重矩阵。这个权重矩阵的作用就是平衡马哈拉诺比斯距离和倾向值距离对计算最后的距离取值时的作用大小。具体而言，在计算遗传匹配的距离时，原始数据需要增加一列，即估计出的倾向值。换句话说，倾向值作为一个新的混淆变量增加到原始数据中去。因此，如果原来的项量是N个元素的话，现在变成了N+1个元素了。而W是这样一个矩阵，它的非对角线元素为0，而对角线元素则是一系列的权重值。这里可以举一个简单的例子，假设有三个混淆变量。那么增加倾向值以后，每个个体的混淆变量增加为4个。假设个体i和个体j之间在原来三个混淆变量上的差值分别为d1，d2和d3，而在倾向值上的差值为dps，则新的距离可以表示为

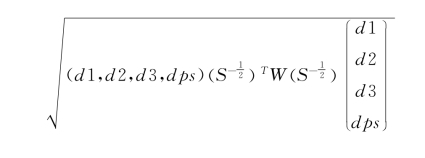
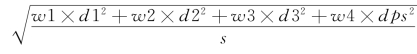暂时我们不去看，W是一个4×4的矩阵，可以表示为。通过代入计算，上面的表达式变为。很显然，如果w 4=0，w 1=w 2=w 3=1，这就是传统的马哈拉诺比斯距离。如果w 4=1，w 1=w 2=w 3=0，这就是传统的倾向值距离。研究者可以通过调整权重的取值来平衡究竟匹配过程是偏向于多变量的马哈拉诺比斯匹配还是一维的倾向值匹配，这就是遗传匹配的逻辑。当然，如果有个别混淆变量很重要，我们可以针对这个混淆变量给一个很大的权重，表示在计算个体间距离的时候，这个变量起到很重要的作用。遗传匹配的这些特征无疑给研究者很大的操作空间。从某种意义上说，这是遗传匹配一个非常好的特征。用这种匹配方法相当于在倾向值匹配和马哈拉诺比斯匹配之间选取了一个中间状态，这个中间状态可以有不同的权重，而这些是我们作为研究者可以设置的。

最后要介绍的匹配方法是和传统的回归模型结合起来，以求尽可能地削减因为实验组与控制组之间混淆变量的不平衡造成的误差（Abadie和Imbens，2011）。从某种意义上讲，这个方法是对一般的匹配方法的修正，故而姑且将之称为回归调整匹配。具体而言，回归调整匹配的思路是这样的。在传统的匹配过程中，对于实验组中的个体而言，他们未能够被观测到的Y（0）是由控制组中的匹配个体的Y平均值来估算出来的。同理，控制组中的个体未被观测到的Y（1）可以由与他们匹配起来的实验组中的个体的Y的平均值来估算出来。假设个体i的匹配对象范围为JM（i），那么分别针对实验组和控制组中的个体，其反事实状态的估计值如下：

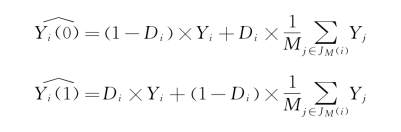
如果我们有一个很好的模型，可以刻画出响应变量Y和混淆变量X之间的关系。则对于实验组中的个体而言，他们未能够被观测到的Y（0）可以用这种“完美”的回归模型的预测值来估算。举例而言，如果在控制组中，有Y=μ0（X）+ε，则我们知道，对于控制组的个体而言，Y的最优的预测值是。此时，对于实验组中的个体i，我们就能够假设，如果他身处控制组的话（反事实状态），他的响应变量取值就应该是。同理，如果在实验组中，我们有模型Y=μ1（X）+ε，那么对于实际上身处控制组中的个体j而言，他的反事实状态（即假设如果身处实验组的话）应该是。如下所示：

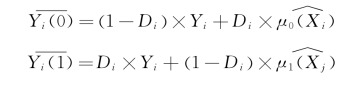
回归调整匹配的思路是将上述二者结合起来。很明显，实验组中的个体i如果和控制组中的个体j匹配起来的话，则j的观测值Yj有可能仍然包含一部分由于i、j在混淆因素X上的差异而造成的系统偏差。此时，如果我们直接以Yj作为匹配材料，则无疑没有剔除出这些系统偏差。一个做法是，从Yj中减去因为Xi和Xj不同而造成的Y的取值差异。此时，如果针对控制组我们有一个很好的回归模型，则这种因为Xi和Xj不同而造成的Y的系统取值差异可以表示为

利用这些估计值，我们就能够进一步修正潜在的实验组和控制组之间的误差，从而尽可能准确地估计出因果关系。