加权法在因果推断中的运用及功能

除了上面介绍的模型法之外，我们也可以用加权的手段去估计Y（1，M（0））和Y（0，M（1））。这就是Hong等人提出的ratio-of-mediatorprobability weighting（RMPW）方法（Hong、Deutsch、Hill，2015）。这个方法的基本思路如下，假设自变量X和中介变量M都是二分型变量，那么它们的取值组合起来有四种情况，如下所示：

表11-2　RMPW方法示意图

对应于这四种情况，我们可以观测到Y的不同取值。这里一定要注意，Y（1，0）是指Y（X=1，M=0）。这个统计量和前面的不同，是可以直接观测到的。比如，自变量可以是教育水平（1=教育水平高；0=教育水平低），中介变量可以是收入（1=高收入；0=低收入），结果变量可以是幸福感得分，那么Y（D=1，M=0）就是指那些教育水平高但是收入水平低的人群的幸福感得分。只要样本中存在这种类型的个体，我们就能直接观测到并基于他们计算Y的平均值。

观察这个表格可以发现，X=1的时候分为两种情况，一种是X=1的时候M=1，即M（1）=1，另外一种情况是X=1的时候M=0，即M（1）=0。这样的话，我们观测到的Y（1，M（1））就有两种可能性，一种是Y（1，M（1）=1），另一种是Y（1，M（1）=0）。如果我们知道M（1）=1的概率和M（1）=0的概率，就能够将Y（1，M（1））写成Y（1，M（1）=1）和Y（1，M（1）=0）的加权平均值，即

这个表达式中右边的每一个统计量都是能够观测出来的，其中M（1）=1的概率实际上就是这类人占整个群体中的比重（在一个样本中，教育水平高同时收入高的人的比例），同理M（1）=0也是如此（在一个样本中，教育水平高同时收入低的人的比例）。Y（1，1）是教育水平高同时收入高的人的幸福感得分，Y（1，0）是教育水平高同时收入低的人的幸福感得分。

按照同样的逻辑，我们有

这个公式可以解释为，那些教育水平低的人的幸福感得分是两部分人的幸福感得分的加权平均，Y（0，1）是教育水平低但是收入水平高的人的幸福感得分，这类人占样本的比例是p（M（0）=1）。Y（0，0）是教育水平低同时收入水平低的人的幸福感得分，这类人占样本的比例是p（M（0）=0）。和上面一样，这些统计量都是直接可以从数据中算出来的。

那么，问题就来了，我们如果照葫芦画瓢，可以写出下面的公式：

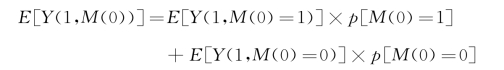
公式的左边是我们希望估计出来的所谓的“矛盾的”统计量，即自变量取值为1，而响应变量M的取值是在自变量取值为0的时候的取值，当然，可以是1，也可以是0。按照加权平均的原则，从单纯数学表达的角度，这个统计量表示为Y（1，M（0）=1）和Y（1，M（0）=0）的加权平均，其权重分别为p（M（0）=1）和p（M（0）=0）。单纯看公式右边的这四个统计量，在数据中我们可以直接算出p（M（0）=1）和p（M（0）=0），其分别为各自样本数占整个样本的比例。但是，我们无法直接算出Y（1，M（0）=1）和Y（1，M（0）=0），因为这两个统计量是矛盾的。在一个数据中，对于那些自变量为1的人，我们看到的它们的响应变量就会是M（1），而不是M（0）。

那么，为了能够计算E（Y（1，M（0））），需要进行一些简单的数学变换。虽然我们看不到Y（1，M（0）），但是能够直接观察到Y（1，M（1）），这两个统计量之间有什么联系呢？可不可以通过Y（1，M（1））来间接估计一下Y（1，M（0））的取值呢？答案是肯定的。(www.xing528.com)

具体而言，针对特定的数据集，我们能够算出来的是Y（1，M（1）=1）的期望值，其估计值是样本均值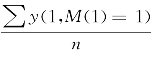。但是我们看不到Y（1，M（0）=1）。不过，我们可以借助加权的思想，来间接估计Y（1，M（0）=1）。比如，将M取值为1的个体看成一个特定的群体，这个群体中的人有两部分组成，一部分是M（1）=1，另一部分是M（0）=1。此时，如果这两部分的人是从这个M=1的群体中随机抽取出来的，那么，我们就能够用M（1）=1的那部分人的Y的观测值来估计M（0）=1的Y的取值。这就好比是从同一个总体中抽取两个样本，只要是随机抽样，样本也足够大，那么一个样本的某个变量的期望值应该和第二个样本的变量的期望值一样，二者都等于总体的均值，这就是大数定理。但是，M（1）=1和M（0）=1这两类人从M=1这个群体中的抽取的概率不一样。前者被抽取出来的概率是p（M（1）=1|T=1），后者被抽取出来的概率是p（M（0）=1|T=0）。那么，我们需要对二者被抽中的概率进行调整。由于抽中概率的倒数是权重，也就相当于作了权重调整，如图11-4所示。

图11-4　加权法原理

对于M=1的这群人，我们按照反事实的逻辑区分出两类人，这两类人有不同的抽中概率，那么他们的权重也就不一样。对于y（1，M（1）=1）而言，我们可以直接观测到，因此无须加权。但是对于另外一种M（0）=1的对象而言，我们是无法直接看到的。虽然如此，我们能够计算权重之比，这样的话，只需要利用权重对比，就能够间接的计算出M（0）=1的情况下，对于y（1，M（0）=1）期望值的估计值，即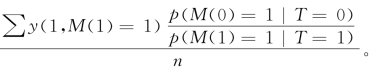

重复上述分析过程，整体的Y（0，M（1））这一矛盾统计量的数学期望，可以表示为

至此，所有的统计量都是可以通过数据计算出来，我们也就能够估计出矛盾的统计量，有了矛盾的统计量的估计值，后续的中介分析就可以直接进行了。在R里，上述的分析可以通过以下代码实现：

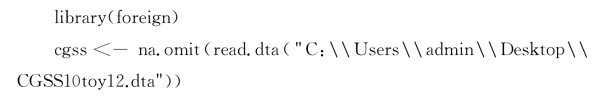
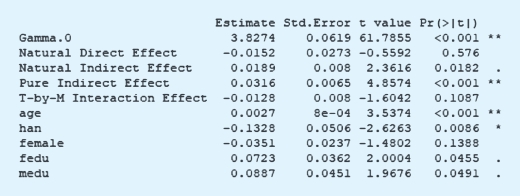
通过上述的结果可以发现，收入水平的确能够起到显著的中介效用。