如何利用细分法解决实验组与控制组的混淆变量问题

传统的回归模型在因果推论上的问题在于研究者无法直接观察到混淆变量在处理变量不同水平下的平衡情况，一个最直接的解决办法就是一一查看混淆变量的平衡性，然后在混淆变量取值一致的情况下（例如都是男性，或者都是城市人口），分别考察因果关系，之后汇总。在混淆变量的数量有限且存在相关的测量的情况下，这不失为一种很好的分析策略。在因果推论的文献中，这种分析方法也称为细分法（subclassification），如表3-1所示。

表3-1　细分法举例

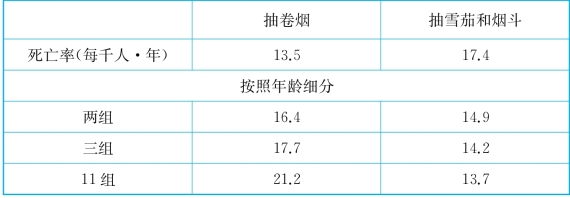
为了展示细分法的主要思路和优势，这里采用统计学家Cochran的一个非常经典的研究（Cochran，1968）。他关心的是抽烟和死亡率之间的关系。具体而言，有两种烟，一种是卷烟，一种是雪茄和烟斗。针对每种抽烟方式，他收集了每千人每年的死亡人数，然后对比。结果发现，抽卷烟的个体的死亡率在13.5‰，抽雪茄和烟斗的个体的死亡率是17.4‰。基于T检验的分析，这两组人的死亡率的组间差异是统计显著的。换句话说，基于这个经验发现，我们可以得出结论，抽雪茄和烟斗的人要比抽卷烟的人死亡率更高。(www.xing528.com)

但是，这个结论肯定存在选择性误差。比如，不同的抽烟方式本身不是随机分配的，不同类型的人选择不同的抽烟方式。我们都有这样的生活经验，年轻人抽烟的话，基本上都是抽卷烟的。我们很难想象一个高中生抽着烟斗或者抽着雪茄走在大街上。但是，一些老人，如果他们抽着雪茄或者抽着烟斗，我们不会有任何违和的感觉。这说明什么呢？抽雪茄和抽烟斗的人，他们的平均年龄应该比较大，而抽卷烟的人，一般平均年龄都比较小。而年龄大有什么风险呢？自然是死亡率高。所以，如果不控制年龄，直接做简单的T检验的话是不行的。基于这个原因，细分法就要把年龄这个重要的混淆变量进行细分。比如，年龄可以是从18岁～80岁的一个区间，那么我们就把这个区间切成几块，在每一块里面看不同的抽烟方式和死亡率之间的关系。可以看到，一开始只是先切两组，比如说年纪大的和年纪小的两组。我们会发现，一开始的结论就被逆转过来了。不是抽烟斗或者雪茄的人，而是抽卷烟的人死亡率更高。如果进一步分三组，分11组的话，我们会发现这个结论是很稳健的，和一开始的结论完全相反：抽卷烟的死亡率更高。实际上，到了切11组的时候，抽雪茄和烟斗死亡率基本上是抽卷烟的死亡率的一半了。

通过这个例子，可以看出细分法的优势所在。在不断细分年龄这个混淆变量的过程中，我们的分析都是在每个切块里面去做的。这实际上就相当于控制了年龄这个变量，因为在一个切块内部，人们的年龄差异不会太大。当然，这种控制并不是完全的控制，因为即使是切块内部，年龄还是有一定的变异的。但是细分法的作用就是压缩年龄这个混淆变量的变异程度。比如，18岁～25岁这个切块内部，虽然被研究对象还会有一定的年龄差异，但这种年龄差异已经非常小了，都是年轻人，因此这种差异不足以造成死亡率的很大变化。但是，如果我们不做细分，就有可能拿一个18岁的被研究对象和一个80岁的被研究对象去进行对比。80岁的人很有可能抽的是雪茄或者烟斗，18岁的人更有可能抽的是卷烟。这个时候80岁的比18岁的死亡率高，我们无法判断究竟是因为抽烟的方式不同，还是年龄的不同，或者二者兼而有之。

综上所述，在细分法中，研究者通过对已知的有限混淆变量的细分，可以很好地去控制它们，从而保证因果推论的无偏性。当然，这里的例子很简单，只是年龄一个混淆变量在发挥作用，如果有两个混淆变量，可以建一个二维的平面，然后对平面进行切割。如果是三个混淆变量，就可以建立一个三维的空间，然后对空间进行切割，以此类推。但是，如果混淆变量数量很多，细分法就会出现问题。当我们不断地去切割的时候，针对每个切块，内部能用的被研究对象就越来越少了。我们可以假想一下，如果一共有300个被研究对象，把混淆变量切成三个切块的话，每一组平均下来就100个人。当然，如果不是平均分配，这300个人里面，有可能200个都是一个切块，这样的话，另外两个切块平均下来每一个只能有50个人了。可以想象，如果我们增加分析的维度，切块的数量会迅速增加，与之伴随的是，每个切块能够被分配到的分析对象的数量迅速减少。这就是我们通常意义上讲的维度灾难。面对这样一个问题，一个解决办法是我们后面要讲的倾向值方法。倾向值起到降维的作用，它可以把所有混淆因素转化为一个数值，然后仅针对这一数值进行处理。

细分法的工作是让混淆因素在实验组和控制组之间达到均衡。这里需要提到的一个问题是，对于均衡，有时候需要分清楚总体不均衡和抽样不均衡。总体不均衡是指实验组和控制组的人彼此之间有一些系统差异，这种系统差异是数据本身的问题，和我们如何获取数据无关。因此，细分法和后面介绍的一系列方法所处理的对象是总体不均衡问题。除了总体的不均衡之外，还有一种不均衡是因为抽样造成的，这就是抽样不均衡。比如，总体里面80%是男的，结果抽样里面50%是男的，这从一个侧面说明抽样本身出问题了。而抽样出了问题，影响的是结论的推广性。总体不均衡的处理解决的是内部有效性的问题，即我们的结论是否足够可靠以反映某种因果性。但是抽样的不均衡解决的是外部有效性问题，即我们的结论在何种程度上可以从样本推广到更多的人。这里细分法谈到的均衡，说的是实验组和控制组要在混淆因素上达到某种总体均衡，和抽样过程没关系。比如，实验组有80%男性，控制组尽量也保持在80%男性，或者说离80%差别不大的一个比例。另一方面，如果统计总体里面80%是男性，但抽样抽出来以后只有40%是男性，这种抽样不均衡不是因果推论直接来处理的。在这种情况下，实验组有可能有20%男性，控制组只要也保证20%男性也可以。如果实验组的男性比例30%，我们也通过细分尽可能保证控制组男性比例也是30%左右。总而言之，如果只是就因果推论谈均衡的话，是不在乎样本里面的比例和总体比例之间的差异的，我们只在乎实验组和控制组之间的均衡。所以说，总体和样本之间，这是一个抽样的问题，控制组和实验组之间，是因果推论的问题。