回归模型的外推问题与随机实验结果的复制

所谓回归法，就是传统的回归模型，比如OLS、广义线性模型等。这种模型的共同点在于，可以将一系列的混淆变量的观测作为控制变量放在模型中，从而起到消除控制变量影响的作用。其可表示为

在上面的公式中，响应变量Y可以表示为处理变量D、控制变量C和随机扰动项e的函数。在此函数中，D的效果就是在控制了C的前提下的效果。

说到回归模型，今天的社会科学量化研究往往会质疑回归模型在因果推论方面的作用。实际上，这种争论在统计学领域里面也是一直存在的。究竟回归模型能否帮助我们建立因果关系呢？Shadish等人在2008年有一篇论文讨论了这一问题（Shadish，Clark和Steiner，2008）。具体而言，他们看的是各种控制混淆变量的方法是否能够复制基于随机实验的结论。其中，基于控制变量的回归模型有很好的表现。换句话说，通过Shadish等人的研究，传统的回归方法在满足一定条件的前提下也是能够复制随机实验的结果，从而给出因果关系的估计。这无疑给长于回归分析的社会科学研究者带来了很大的信心。这个研究过程如图3-1所示。

图3-1 随机实验设计验证回归模型效果

研究者共找到455个学生，通过随机安排的方式，235个学生进入随机实验组，210个学生进入观测研究组。然后，随机实验组再进行第二次随机安排，有的学生随机接受口语训练，有的学生随机接受数学训练，这就是一个很典型的随机实验了。与之对比，在观测研究组，实验人员让学生自选是否进入口语训练还是数学训练。当然了，一旦允许被研究个体自选，他们背后的各种社会因素都会起作用，比如说男生怎么选，女生怎么选，城市人口怎么选，农村人口怎么选，各种复杂因素的不同组合都会有各种影响。基于这种研究设计，我们发现，第一步区分随机实验组和观测研究组的时候是随机安排的。因此，这两组的研究设计（一组经过二次随机安排不同的训练，一组通过自选进入不同的训练）具有可比性。最后发现，通过各种各样的观测性分析操作（包括多元回归）得到的结论和随机实验（第二次随机）研究得到的结论是非常近似的。因此，即使是在因果推论的研究中，可以说回归模型也是有价值的。在实践操作过程中，通常而言，研究者只要能够有效地把混淆因素通过回归模型控制起来，得到的结论就是和随机实验的结论实质上趋近。区别可能只是一个得到的点估计值是5.1，一个得到的点估计值是6.1。但二者都是统计显著的，而且符号一致。这对于大多数社会科学研究而言，已经足够了。这是因为我们很多时候不是特别在乎具体的数值，而是看数值所反映的实质结论。例如，这个系数是不是在常规的显著性水平上显著，系数是正还是负。原则上讲，只要系数正负方向和统计显著性是一样的，我们基本上会认为二者的结论一致。

虽然这个研究给我们一定的信心，但回归法依然有一个不得不面对的问题：外推（extrapolation）。什么叫外推呢？这里举一个例子（如图3-2所示）。在散点图上有三个点，我们基于这三个点做了一个回归模型。当X取值是x1的时候，Y的取值是什么呢？很多时候，我们倾向于给出基于回归模型做的预测值y1。但是如果退一步仔细想一下，我们怎么知道X取值为x1的时候，它的Y值就一定是y1呢？得出这个结论，依据是什么呢？依据可能是回归模型的拟合优度。比如图中的回归模型，所有的观测点都在回归线上，我们很难得到一个更好的模型了。此时，我们会说，这个模型拟合的那么好，那么对X取值为x1时，Y的取值的最好的猜测应该就是y1了。但是，实际上在图中阴影部分的区域是一大片空白。换句话说，没有任何资料来告诉我们这部分的数据区域中X和Y的关系的基本模式。有可能是曲线a的关系，也有可能是曲线b的关系。实际上没有办法从经验上去确定X和Y之间在阴影部分就一定是线性关系。此时，利用别的数据点建立的模型去推广到没有直接数据支撑的部分，就是所谓的外推。

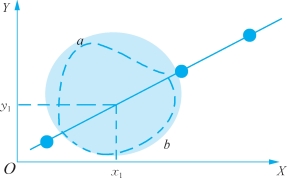
图3-2　外推举例

对于经验研究而言，外推是我们经常使用或者默认的方法。但是在一些具体的研究中，外推有可能带来问题。打个比方，这就类似于医生找了一些病人拟合了一个模型来确定药效，然后把这个结论用到一些新的病人身上。有时候这样做没有问题，但是万一这些新的病人和医生建立结论依据的那些病人有系统差异呢？有没有可能，医生的药对建立模型的这些病人有很好的效果，但是对新的病人毫无疗效甚至有反作用呢？某种意义上，这也是为什么任何药品出来后都要超出实验室的范围进行临床研究，以便最后把药效尽可能推广到一些没有实验涉及的人群身上。

在我们平时的研究中，很多时候没有意识到外推的问题，但这绝不意味着外推的问题不存在。这里我可以举个例子。假设一共有三个变量：是否上大学、收入情况和性别。我们都知道，在分析上大学和收入关系的时候，性别是一个很重要的混淆因素，女性相对男性在上大学机会上有劣势，而同时女性相对于男性而言在劳动力市场也有劣势。如果我们不控制性别，而只是简单地看上不上大学和收入的关系，这个结论是存在潜在的选择性误差的。面对这种情况，理想的数据信息应该是这样的，做一个2×2的表格，分别对应上不上大学和男女性别（如图3-3所示）。然后在每一个横的两组之间做对比（分别计算b-a和d-c），然后再算它们的加权平均。我们得到的就是在控制了性别以后上不上大学对于收入的影响。

(www.xing528.com)

图3-3　上大学和收入关系的外推举例

比如说，男性中上大学的人的平均收入b是100，不上大学人的平均收入a是80。女性中间上大学的个体的平均收入d是80，不上大学的个体的平均收入c是60。如是男性女性人口比例是一样的，最后上大学对收入的影响就是（100-80+80-60）／2=20。

那么，如果所有的女性都不上大学，上大学的人里面都是男性的话，我们的分析能不能进行下去呢？答案是否定的。因为这个2×2方格中少了一个方格的信息，我们因此不能计算针对女性的大学回报，自然不能计算后续的加权信息了。按照这样的设计，随机产生了一些数据，如图3-4所示。

图3-4　外推举例之假想数据

这个数据中，女性（gender=0）上大学（college=1）的人数为零。如果我们希望分析在控制了性别后大学教育的收入回报，这个分析理论上讲是没有办法进行下去的。但如果把这个数据放到STATA里面去分析，会发现STATA仍然会报告一个结果。

那么STATA怎么算出来这么一个遗漏方格的信息从而计算出上大学能够带来20.5个单位的收入的提升呢？实际上，这里就是外推在起作用。这里可以认为这三个变量构成一个三维空间。那么，空间上有一些空白点。但是，基于已有数据构成的平面基本上取代了空白点，从而把模型信息代入到空白点的地方。以这个例子中的数据为例，我们把它们画到一个3D散点空间中，如图3-5所示。可以看到，在四个支柱处，有三个都有数据点支持，但是有一个缺乏数据。但是这并不妨碍回归模型设置一个回归平面，并基于这个平面和缺乏数据点的支柱的交叉来“外推”到那些实际不存在的上大学的女性的平均收入水平，如图3-5中点A所示。和上面的二维例子一样，这个点A的信息基于的是模型的外推，而在这个支柱的位置上是没有任何经验信息的。但是很遗憾，这种外推的应用是软件默认的操作，我们并没有办法直接从模型结果中检查出来。

图3-5　外推举例的三维分析结果

外推对于因果推论而言，最大的问题在于结论有可能不是数据的经验模式，而是混杂了基于模型对于未知数据区域的猜测。究竟猜测的数值为何，自然取决于拟合的模型是什么样的。正如上面的二维数据的例子中展示的，线性模型和曲线模型对于未知区域的数据模式的猜测是不同的，自然结论也不同。我们对于因果关系的推论就很大程度上取决于模型的形式。形式不同，估计值就不同。也就是说，我们的结论很不稳健。

从另外一个角度来讲，上面的问题也就是因为我们没有办法去严格地控制性别。换句话说，性别这个混淆因素在上大学和不上大学之间是高度不平衡的。在随机实验一章中，我们已经谈过，随机实验的优势在于能够将混淆因素在实验组和控制组之间拉平，从而保证混淆因素的平衡性。也就是说，除了混淆因素外，只有处理变量的取值在实验组和控制组之间有所不同。但是上面这个例子，性别作为混淆因素明显在大学组和非大学组之间不平衡：男性占了100%，而女性是零。那么，我们估算的因果关系就有瑕疵，因为实际上根本就没有任何经验信息告诉我，女性的大学教育的经济回报是多少。所以，这看似控制了性别的大学教育回报研究中，性别因素实际上是在上不上大学的两组人之间不平衡的。在STATA中，虽然统计结果告诉我们性别对于收入没有显著的影响（p值是0.34），但由于性别没有办法在实验组和控制组之间达到平衡，这里所谓的控制的性别是一个假的控制。

综合上面的例子，我们可以认为，在做社会科学研究的时候，完全可以用回归模型去做因果推断。但要时刻注意的一点是，有可能在回归模型中，虽然放了很多控制变量，但这些控制变量在实验组和控制组之间并不平衡。一旦出现这种情况，我们的回归结果就有可能不能做因果性的诠释。因此，单单去看统计输出结果有时候是有问题的。比如上面的输出表格，模型的R方能达到71%，这对于一般的社会科学研究而言，可谓完美了。可惜的是，这么完美的一个分析结果，如果从因果分析的角度来讲，却是站不住脚的。