如何分析随机实验数据的方法与应用

上文提到，基于随机实验得到的研究资料相较于基于观测性研究的资料而言，具有比较简单的分析过程。由于相关混淆因素对于响应变量的影响都能够通过随机化的过程拉平，因此研究者只需要将关注点置于处理变量之上即可。在现有的研究实践中，我们有两种分析随机实验数据的方法。第一种方法就是T检验。第二种称为费舍尔精确检验（Fisher's Exact Test）。这里用一个简单的例子来说明两种方法的异同。

假设目前一项研究中有六个研究对象，给他们随机分配一些教学项目，一部分人分配到新的教学项目里，一部分人分配到旧的教学项目里。他们在不同的教学项目里待了一个学期以后看他们的考试成绩，如图2-4所示。

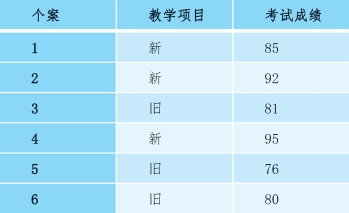
图2-4　随机实验举例

按照T检验的分析思路，我们看的是新教学项目组的个体的平均成绩和旧教学项目的个体的平均成绩之间究竟有没有显著性差异。假设“1”代表了新的教学项目，“0”代表了旧的教学项目，在这六个被研究对象中，处理变量的取值就是1-1-0-1-0-0。用传统的T检验分析，采用以下R代码，得出分析结果。

p值是0.039 62，说明这两组之间是有显著差异的。

在STATA中，类似的T检验也可以操作，代码如下。结论与这里的一致，不再赘述。

关于T检验，这里还是有一些地方需要说明的。T检验的来源是尼曼（Neyman）的重复抽样检验。从因果推论的角度来看，处理变量对于响应变量的影响，也就是我们关心的因果关系τ，可以表示为

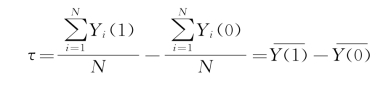
而对它的估计量则是

即组间均值。可以证明，这个估计值是无偏的，也就是说，E（τ^）=τ。

至此，这与传统的独立样本T检验一致。但是，在传统的独立样本的T检验里，两组均值差异的方差是实验组的方差比上实验组的样本量大小，加上控制组的方差比上控制组样本量的大小。但是，基于严格的数理推导，实验组的均值和控制组的均值之差的方差实际上有三部分组成，一部分来自实验组，一部分来自控制组，第三部分来自二者的协方差，表示如下：

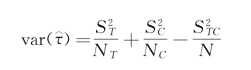
之所以有协方差存在，是因为我们将实验组的人看作Y（1）的观测，控制组的人看作Y（0）的观测，但是对于同一个个体而言，Y（1）和Y（0）肯定是相关的，因此我们假想同一个人分别放入实验组和控制组后，他们的取值应该有一定的联系。例如，一个老人放入实验组后的症状表现和他放入控制组的症状表现应该有联系，这种联系来自这同一个个体的生理情况。因此，在计算组间均值差值的方差的时候，严格来讲需要减掉一部分的协方差。但是问题在于，这部分的协方差无法直接计算。如果想计算出协方差部分，需要同时知道Y（1）和Y（0），当然，这是无法满足的（因果推断的基本问题）。正因为如此，如果采用传统的T检验方法来做因果推论问题，所使用的方差实际上是被夸大了的。简单地假设Y（1）和Y（0）彼此独立，也就是认为协方差为0，但是严格的计算过程还需要减掉一个正数的。也就是说，虽然这里的p值是0.039，但如果真的把没有看到的协方差考虑进去的话，p值会变得更小一点。

对于T检验而言，研究者关心的问题是，实验组和控制组的均值是不是一样。但我们都知道，均值这个统计量很多时候并不可靠。在算平均收入的时候，把一个富翁拉进来，一下子整体显得平均收入很高，但实际上这种很高的平均收入隐藏了内部的不均衡，所以平均收入不是一个很好的指标，其对于极值的影响反应是很大的。那么相比于T检验，一个替代方案就是费舍尔的精确检验方法。和尼曼不同，费舍尔的假设可以称得上强（strong）零假设。对于尼曼的T检验而言，零假设是组间均值相等（例如，μ实验组=μ控制组）。但费舍尔而言的零假设更加强，是指对于每个个体而言，处理变量没有任何效果（例如，Yi（1）=Yi（0））。也就是说，尼曼看的是处理变量的组间效果，而费舍尔看的是处理变量对于个体的效果。因此，费舍尔的假设较之尼曼而言更强，故而叫强零假设。

基于这样一个强零假设，后续的工作就和尼曼的思路有所不同了。传统的T检验要通过零假设建立一个零分布，如果我们知道零假设下的统计量是一个正态分布，那么就能够看极值部分（尾部）的面积，这就是p值。我们也要建立一个基于零假设的零分布。由于尼曼的思路是反复抽样，因此我们通常认为零分布是正态分布。但是在费舍尔这里，并不假设零分布服从任何已知的分布形态，而是基于排列组合来构建“经验”零分布。我们还是回到刚才的教学项目的例子，基于强零假设的话，这个教学项目对于“每个人”来讲没有任何效果。因此，一个人进入哪一个教学项目组，应该不会改变其成绩。比如，这里的1号，他实际上分配的是新的教学项目组，他的考试得分是85分。那么，如果这个教学项目对他没有任何作用的话，同时如果他当时分配在一个旧的教育项目组的话，他的成绩是多少呢？还是85分。这时候就可以把这六个教育项目重新分配，然后就得到一个新的成绩，如图2-5所示。

图2-5　随机实验举例之强零假设状态

可以看到，4号和5号还是分配在原来的教学项目，但1号已经到旧的教育项目组了。虽然分配到旧的项目组里面，但他的考试成绩应该还是85分。由于这里的85分不是我们直接看到的，而是基于强零假设推论的，因此加了括号。以此类推，每个人都做了类似的工作。基于这个新的表格，可以计算新的教育项目组和旧的教育项目组之间的组间均值差异。如果看原始数据，组间差异是11.67分。但重新洗了一遍牌，再做一个分配的话，得到的组间差异就不一样了。换句话说，这时候再看新的教学项目组和旧的教学项目组的均值差异就不一定是11.67分了。如果把这6个教育项目组不断去洗牌，那有几种排列组合呢？可以算出来，是=20，如图2-6所示。

图2-6　随机实验举例之所有排列

针对每一种排列，都可以计算一下新的教育项目和旧的教育项目之间的均值差异，从而得到一个差值的分布，这就是基于强零假设的零分布了。这时候我们再把实际计算得到的11.67分放在这个分布上。可以发现它在一个很极端的位置，由此我们就可以把零分布拒绝，即拒绝强零假设。如果在R里面做的话，可以把处理变量的分配做一个排列组合，从6个人里面取3个，分成实验组、控制组，针对每一种组合做一个简单线性回归（类似于计算组间差异），得到一个回归系数。这时候再把观测到11.67的点在这上面标注出来。代码如下：

具体的分析结果如图2-7所示（此为零分布）。

图2-7　随机实验示例分析结果(www.xing528.com)

在零分布上右边的一条竖线代表了观测到的11.67。这条线在一个很极端的位置上，那就说明，这个11.67是真的很大的一个数字，而不是通过随机的排列组合就随便能得到的。因此，可以得出结论，这两个教学项目的确对学生的成绩有不同的影响。

在STATA中，我们可以进行类似的分析，代码如下：

经验结论与这里的一致，11.67的观测值是比较极端的。

这里插一句题外话，费舍尔当时是怎么想到这么一个“聪明”的主意的呢？他这个思路来自很有名的叫做女士品茶的实验。当时一位英国老太太说，英国茶和牛奶，先放牛奶和先放茶，它的口味是不一样的。当时很多人不相信，茶和牛奶混在一起了，谁先放谁后放有什么区别呢？但费舍尔想到这么一个方法来测试这个老太太是不是真的能够判断出口味的差异。遵循同样的逻辑，比如说让这位老太太连喝六杯茶，三杯是随机先放奶后放茶，三杯随机先放茶后放奶。喝完以后让这位品茶的人判断这六杯茶哪些是先放奶，哪些是先放茶的，以此计算她的正确率（比如其正确率为70%）。这里要问的就是，她如果靠猜能不能达到70%的正确率呢？如果她靠猜就能达到70%，那就说明她根本没有这个辨识能力的，但如果靠猜“很难”达到70%，那就说明她确实有这个辨识能力。那问题是怎么判断她是不是猜的呢？费舍尔就用了强零假设的逻辑。如果她是猜的话，对于这位老太太而言，先放茶和先放奶，她给出的答案应该都是一样的。同理，列举出各种排列组合，最后得到了零分布。基于这个分布，看老太太实际的70%的正确率所处的位置。如果她的正确率的数值在零分布上处在一个很极端的位置上，那说明她很有可能不是猜的。因为如果靠猜的话，很难达到这么高的正确率。但如果70%的正确率在分布的中间位置，那就说明随便猜一下就能达到70%的正确率，自然不能说老太太有很高的品鉴能力。

在社会科学研究中，也有类似的分析思路。例如，一项研究探索了美国各个县宗教组织的多样化程度和当地居民宗教参与情况的关系（Voas，Crockett and Olson，2002）。他们可以用赫芬达尔指数计算多样性，用各个县信教居民的比例计算宗教参与情况。基于观测数据，每个县都能计算其多样化程度和宗教参与情况，以此知道二者的相关程度，这是观测到的信息。那么为了进行费舍尔精确性检验，研究者可以把这些宗教组织在不同县之间进行重新排列，就像洗牌一样。每洗一次牌，就计算一下宗教多样化程度和宗教参与情况之间的关系。在多次洗牌之后，我们得到基于强零假设的零分布，然后就去看观测到的二者之间的关系在整个洗完牌之后得到零分布上关系的位置，这是一个很好的分析思路。而这个思路也直接将我们引入到排列检验（permutation test）这一方法。所谓的排列检验，指的是不一定要穷尽各种潜在的组合，而是每一个重新对处理变量的分配进行排列，然后计算这种随机排列下的所谓处理效应。在多次排列后，我们就能够建构类似于强零假设那样的零分布，以便进行假设检验。例如，我们如果想知道教育和收入的关系，并对其进行排列检验，可以采用以下代码：

可见，教育和收入之间有着显著的联系。

在STATA中，类似的分析通过以下代码实现：

＃从后面的回归模型中抽离出edu4的系数b＃

由于p值小于0.001，我们可以说，教育水平的确会对收入产生显著影响。这一结论是通过非参数的排列检验得来的，其中没有任何对零假设分布形态的规定（我们不要求正态分布）。

基于排列检验，我们可以进一步引入控制变量。罗森鲍姆（Rosenbaum，1984）指出，如果存在控制变量，我们可以对排列检验的统计量进行调整，以控制这些控制变量的效果。假设各个控制变量构成的矩阵为X，那么定义M=I-X（X′X）-1X′，则在去除控制变量影响后的统计量可以写为

还是接着上面的例子，假设我们希望控制年龄、民族、性别、父母教育水平、年龄平方、父母的户籍状态，可以采用以下R代码：

结果发现，教育水平在控制了一系列的控制变量之后，还是显著地和收入相关，如图2-8所示。

图2-8　有控制变量的随机实验示例分析结果

在STATA中，我们的操作相对而言比较简单，代码如下。结果还是统计显著的。

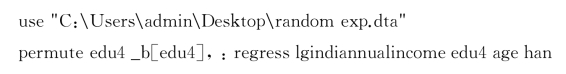
到目前为止，我们已经介绍完了随机实验的基本原理和分析方法。从本质上看，随机实验的方法并不复杂，它的所有工作都取决于研究者能不能把感兴趣的处理变量随机地分配到不同对象上。如果一个研究的主题可以做随机实验的话，一个建议是尽量做随机实验，这样的话，后续的分析会非常简单。美国20世纪在经济学领域就有过这方面的讨论，也有文章论证不是实验的研究结论都不可靠（Lalonde，1986）。从这些争论以后，美国政府的很多决策都尽量去进行随机实验，这给研究者提供了很多的便利。同时，这些举措也让随机实验方法日渐深入人心。举一个例子，选举的时候，候选人的信息印在宣传手册上的第一页和最后一页可能有不一样的效果。所以美国加州采取随机分配的方法安排候选人在宣传手册上的位置，从而使得发到每个投票人手里的宣传手册可能各不一样。同一个候选人，有的印在第一页上，有的印在第三页上，等等。通过这样的设计，研究者就能够知道宣传手段对选举结果有什么影响（Ho和Imai，2006）。此外，还有一个很有名的随机实验的例子，美国去越南打仗的征兵过程采取抽签的方式进行，比如说123456，抽中456上前线，抽中123回家不用打仗（Angrist，Imbens和Rubin，1996）。这些操作听起来好像是游戏一样的，但正是因为有这样操作，给了后续社会科学家们很好的研究机会。

目前，我们在国家层面上的政策进行随机实验的并不多。但是一些区域性政策的实施也日渐有随机性安排在里面。比如，北京的抽签摇号拿车牌。我们假定它是随机的，那么就可以看拿到车牌的因果效果。实际上很多经济学家用工具变量的方法来做，他们认为随机获取车牌是一个很好的工具变量。但此类研究一个潜在的问题是，我们虽然找到了很好的随机安排，但很难找到有社会意义的Y。换句话说，拿到车牌的和没拿到车牌的人相比，我们究竟希望比较什么Y呢？和摇号拿车牌不一样，摇号上战场，有很多我们可以研究的实际问题，比如说上战场以后就不可能去上学，那人力资源积累就少了，是不是退伍回来以后工资就比那些没有上战场的低。这个问题具有很重要的现实意义，但是通过摇号分车牌，我们的研究却容易找不到被车牌影响的有实际意义的Y。