药物对感冒痊愈的因果关系定义及其影响

我们进入第一个问题，什么是因果关系。这里举个例子，大家都有感冒的经历。感冒了以后需要吃药，吃药以后感冒好了，这个时候我们就会说，多亏吃了药，不然的话，感冒还不知道什么时候能好。在这个日常生活的例子中，实际上一个人在吃药和感冒症状变化之间确定了一种因果联系。但这种生活化的语言并不严谨。例如，我们怎么就知道感冒好了就是因为吃药了呢？比如说小朋友们感冒，只要不是病毒性的，让他坚持一星期，不吃药感冒也有可能好了。这时候，如果当时给他吃药，他感冒自然会好，但是即使不吃药，感冒也会好。这时，我们如何判断吃药对减轻小朋友的感冒症状的因果性联系呢？如果不吃药感冒也会好，我们会认为，吃药和感冒痊愈之间没有什么因果关系。从这个角度看，当我们说吃药和症状痊愈两者之间有因果关系的时候，我们实际上有一个基本预设，即“如果当时不吃药的话，感冒不可能好起来”。只有吃药以后，症状才得到缓解。从这个例子可以发现，对于一个个体而言，有两个状态，这两个状态都是一开始吃药之前不知道的，一个状态是吃了药以后的状态，另一个状态是没有吃药的状态。只有这两个状态有所不同，我们才能说是因为吃了药，感冒才好的。

这里我们可以再举一个社会科学经常分析的例子。我们之所以上大学，一个很大的动力是，毕业以后收入会不错。也就是说，我们都觉得上了大学以后的社会经济地位要比不上大学的情况下更高。换句话说，我们来上大学，一般会抱有一个预设，认为“上了大学拿到文凭后，到劳动力市场上去找工作，收入水平肯定要比那些不上大学、高中毕业后就直接进入社会的要高”。但是我们如何能够确证这一点呢？为什么上大学就一定让我们的收入提高呢？会不会出现相反的情况，上了大学反而比不上大学收入更低呢？为了回答这些问题，我们通常的做法是，通过列举一些身边人的例子来说明上大学的好处。比如，一个人可能会说，某某同学，他高中毕业进入社会，到现在还没有稳定的工作、收入微薄。而另一个某某同学大学毕业了以后工作稳定，收入可观。但问题在于，这些某某同学是“你”吗？当然不是。那么下一个问题是，如果“你”当年不上大学，会是什么样的境遇呢？一定就和这个无稳定工作的某某同学一模一样吗？这可能就要画一个问号了。很多时候你会说，我也不知道啊，因为我实际上已经上大学了，没上大学的情况谁知道呢。此时，你虽然可以想象，但是也确实无法确证，如果“你”当时没上大学，而是直接进入社会，有没有可能比如今上大学的“你”的境遇更好。也有可能，“你”大学毕业以后去公司上班，但如果当年没上大学的话，反而自己开公司，成为雇佣大学生的人了。如果是这样的话，你的结论就会有180度转弯，即上大学没有那么有价值，甚至“有损”个人利益。大学回报问题是很经典的因果推断问题，这在讲到倾向值和匹配方法的时候，会再拿出来讨论。这里提到这个例子，是希望说明，和感冒吃药的例子类似，我们在思考因果问题的时候，需要思考个体的多种状态，唯有如此，我们才能够了解某种处理变量（这里的是否上大学）对于某个响应变量（这里的社会经济地位）的影响。说到这里，读者都能理解，毕竟是大家都耳熟能详的事情，有什么稀奇的呢？为了回答这个问题，我们需要进行更加规范、严格的讨论，以此展现上述的思路的价值，这就涉及反事实（counterfactual）问题了。

首先来定义什么是反事实。从本质上讲，事实状态，就是我们自己可以看到、经历了的状态。在感冒吃药的例子中，事实状态就是你真的吃药以后的症状。在教育回报例子中，大学毕业后的收入情况就是一个事实状态。而反事实状态则指的是，处理变量取值为“现实生活中没有发生”的状态下，响应变量的取值。也就是，如果一个人没有吃药的情况下会有什么症状，或者如果一个大学生当年如果没上大学的话，他或者她的收入情况。基于这些定义，我们很容易理解，事实状态和反事实状态的差异，即代表了某种因果关系，即某一个处理变量对个体的因果效果。

为了便利后续的讨论，这里有必要引入一些符号。假如说我们关心的响应变量标注为Y，处理变量为D。那么，Y就是D的一个函数。如果D有两个状态，即上不上大学（D=1表示上大学；D=0表示没有上大学），Y是收入，那么每个个体有两种状态，一种状态是他上大学以后的收入Y（1），一种状态是他不上大学的收入Y（0）。针对个体i，我们可以分别表示为Yi（1）和Yi（0）。需要提醒大家的是，为了更好地理解Yi（1）和Yi（0）的含义，这里要把我们手里的调查资料或者数据先放在一边，考虑的不是经验事实如何，而只是在理念上进行想象。这里之所以在Y后面采用括号，表示的是Y“不是”一个真实的事实状态，而是我们假想的状态：如果D取值为某个值的话，Y的取值如何。与Yi（1）和Yi（0）相比，Yi没有括号，因此这个符号表示我们真实观测到的个体i的Y的取值。比如，大家从某个调查数据中找到一个人，看到他的收入情况，就可以用Yi来表示。对于个体i而言，因果效果τi可以表示为

那么Yi，Yi（1）和Yi（0）三者之间是什么关系呢？这里，我们可以将Yi写成Yi（1）和Yi（0）的函数：

如上文所述，Yi表示实际上的观测值，这个D是0或1，1的话是上大学，0的话表示不上大学。基于上面的公式，如果一个人上大学了，则D=1，后面不上大学的情况就不存在了（1-1=0），Yi就等于Yi（1）。同理，那些没有上大学的人，其观测值就是Yi（0）。通过这个函数关系，我们可以认为，当处理变量D为二分变量的时候，每个被研究对象都有两个状态，如果上大学其收入怎么样，如果不上大学其收入怎么样。基于这个基本的设定，研究者收集数据，找了一些上大学的人，一个人的收入情况Yi就应该等于他或者她“如果”上学的话的Yi（1）收入情况。对于那些实际上没有上大学的人，Yi的观测值就是如果该个体没上大学时候的Yi（0）收入情况。对于上大学的人而言，Yi（0）即为其反事实状态，因为这一状态不可观测。同理，对于那些没上大学的人而言，Yi（1）即为其反事实状态。

这里不难发现，Yi（1）和Yi（0）是不可能同时观测到的，即反事实的两种状态并不能直接观察到。这被称为“因果推断的根本性问题”（Holland，1986）。这个根本性问题带来的最大困境，在于我们无法直接计算个体性的因果关系，即针对个体i而言，上不上大学对于他或者她的收入的影响是无法直接计算的。这里先简单提一下，面对这个困境，一个替代性的方案是，找一些和被研究对象“特别像”的人，他们不知道什么原因，比如说高考的时候因为突然发烧或者其他一些意外情况，没能够上大学，但他高考之前和被研究对象很像，例如成绩接近，也是班级前几名的，性别都是男（女）的，都是城市户籍，等等。但实际情况是，被研究对象上了大学，而与之相似的个体没能上大学。经过四年，我们把他们进行对比，如果发现收入差不多，此时我们会说，好像上大学没什么用。如果上大学的个体收入更高，那么我们会得出结论，上大学的确能够提升个体的社会经济地位。但无论结论是什么，之所以能够得出一个因果性的结论，是因为那个和被研究对象相似的高中同学可以近似地代表那个如果当年没有上大学的被研究对象的情况。在本书后面章节介绍的很多具体的因果推论方法都是遵循了这一思路，即找到和被研究对象近似，但是处理变量D取值又不同的人来作为探究反事实状态的凭借。

在确定了因果关系的基本定义之后，下面就要对因果关系进行进一步的分类。具体而言，有三种估计量。一个估计量叫做ATT，一个叫做ATU，一个叫做ATE。ATT全称是实验组平均因果处理效应（average treatment effect for the treated），是针对那些接受处理变量影响的个体的因果效果。举个例子，研究者手里有一些数据信息，包括一些已经上大学的人，同时研究者知道他们的实际收入情况。此时，研究者想知道“这些大学毕业生”当年如果没上大学的话他们收入情况是怎样的。用他们的实际收入减去如果没上大学的情况下的收入情况，此时就能够知道上大学对于“大学生们”的影响，这就是所谓的ATT。用公式表示如下。其中，我们严格限定样本为D=1的人，n1表示D=1的人的个数，

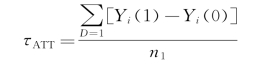(www.xing528.com)

ATU全称是控制组平均因果处理效应（average treatment effect for the untreated）。回到上面的例子，我们收集的数据中包括一些真的没上大学的个体，我想知道如果他们上大学了以后的收入情况，然后用这些假设的反事实收入信息减去实际的收入情况，就知道上大学对于“没上大学的人”的收入的影响，这就是所谓的ATU。和上面的公式类似，我们限定分析对象为D=0的人，这些人的总数是n0，

综合ATT和ATU可以发现，可以把整个分析样本分成两部分，一部分是D=1，一部分是D=0。D=1的这部分人是上大学的，D=0是没有上大学的，ATT针对的是D=1的这部分人，ATU针对的是D=0的这部分人。对于这两组人，分析思路实际上是一样的。ATT是说，一个人确实上了大学，那么我想知道如果这个人没上大学的收入情况，以确定大学教育对于此人收入的影响。ATU是说，对于没上大学的人，我想知道如果他们上大学的话，收入情况是什么样的。

对比ATT和ATU可以发现，对于大多数的研究而言，ATT要比ATU重要得多。为什么呢？因为ATT涉及的这些人是“真正”上了大学的，也就是真正接受了处理变量影响的人，而ATU针对的是根本没有接受任何处理变量影响的对象。也正是在这个意义下，很多社会科学的研究者会认为，ATT反映了某种政策效果。例如，假设一项研究的处理变量是是否参加一项找工作的技能培训。如果你是这个培训项目的设计者，你肯定想知道这个项目对于“真的参加培训的人”而言，是否起到帮助他们找工作的效果。换句话说，你想知道的是对于这些已经接受培训的人而言，这个培训是不是有用。相比较来说，你不是那么想知道，从大街上随便拉一个没有接受过培训的人，假设把他放到培训项目里，是不是对他找工作有所帮助。这是ATT和ATU两种不同思路的体现。实际上，这就好比你是一个医生，你肯定想知道某个特定的药物究竟对需要这个药并服药的病人有没有用。所以说，ATT的估计值有政策上的实际价值，而ATU很多时候是缺少政策价值的。

虽然这样说，但是对于一般的社会科学研究而言，很多时候我们不做政策评估，而是希望确定了一个“一般性”的因果关系，即确定一种因果机制。此时单纯地关注ATT而忽视ATU就不合适了。正因为这个原因，很多社会科学的研究主要报告的是ATE，全称为平均因果处理效应（average treatment effect）。ATE如何计算呢？很简单，刚才这里大家也看到了，ATT是针对D=1的这部分人的因果效果，ATU是针对D=0的这部分人的因果效果。想知道整体的因果效果ATE，就只需要做一个加权平均就可以了。看一下D=1的这部分人占总体的比例WATT，以及D=0的这部分人占的比例WATU，就得到了一个整体的因果效果ATE，

到目前为止，我们已经介绍了基本的因果推论术语和符号。为了表述方便，这里可以暂时忽略个体标注i，来作一个简单的总结。Y（1）和Y（0）指代的是一些潜在的状态，它们彼此为反事实状态。针对每一个分析对象，他们都有这两个取值。而基于实际上D的取值，我们可以得到Y的实际观测值。ATT、ATU和ATE是针对不同群体的因果效果，ATT针对的是D=1的个体所体现出的因果效果，ATU指的是D=0的个体所体现出的因果效果，ATE则是数据整体的因果效果。

这里有必要区分以下Y（D=d）和Y|D=d。这里的竖线表示的是给定某种状态，d是D的某种具体取值。Y|D=d是指在现实的数据中，实际观测到的特定群体的Y值。例如Y|D=1是指那些真的接受了高等教育的人的Y取值。同理，Y|D=0是真的没有接受高等教育的个体的Y的取值。所以说Y，Y|D=1，Y|D=0三者都是基于已有的观测数据“实实在在”看到的数值。而Y（1）、Y（0）则是看不到的潜在的一个状态。采用图示法，如图1-1所示。

图1-1　潜在事实状态示例

在图1-1中，所有数据点都有Y（1）和Y（0）两种状态。但是如果看具体的观测值的话，则Y|D=1和Y|D=0将全部数据分成了两个部分，即实际上是否接受处理变量的影响。