网络中作者重要性计算优化方案

不同类型作者关联网络的相关性主要是研究网络与网络间的关系，因此，针对每个作者节点计算其重要性在分析过程中并不是主要内容，而对内部结构进行分析时，则必须对每个作者的重要性，依据其所在的网络结构获取重要性的得分。相对于局部的重要性计算方法，节点的全局重要性计算方法更能反映在整个网络中节点的重要性和地位，对于资源创作者的聚合，这种全局性的重要性也更有价值。以特征向量中心性为代表的全局重要性在一定程度上可以摆脱中介中心性、接近中心性等间接评价所造成的失真，同时，也可以使得度数中心衡量过于粗糙和无区分度的问题得到解决。

相对而言，特征向量中心性在作者关联网络中的适用度较高，这是因为作者关联网络中客观上允许存在回路，例如作者之间的引用关系，时序上的累计数据形式导致两个节点之间可以存在双向关系，这就和这些算法开发的网络环境更加类似。对应的，同时也可以将其他无向有权的作者关联网络例如合作、共被引等当成是双向对称的网络，同样适用这些算法。这些有效性已经得到很多论证，因此可以直接适用于作者关联网络。特征向量中心性的常见重要变形包括PageRank算法和HITS算法。HITS算法最初由康纳尔大学的计算机专家克林伯格所开发^[19]，相较于HITS侧重于为独立的查询进行单独的计算，PageRank算法则更倾向于反映网页本身的特征，即对整个网络中的网页进行排序^[20]。PageRank算法的典型应用是目前全世界最大的搜索引擎谷歌，在提出PageRank算法的最初那篇文章中，开发者引用了加菲尔德关于引文分析的基本思想。PageRank在作者关联网络中已有广泛的应用成果，因此本研究对6种作者关联网络中的节点重要性计算采用PageRank算法。

PageRank的基本理念可以表述为：入链数是评价页面重要程度很好的指标，且来源于主要页面的入链数比来源于次要页面的入链数更能说明重要性。其数学表达如公式6-4所示：

其中，N指整个网络中页面的数量，d是一个阻尼系数，pi指页面p的反向链接数，C(pi)是pi的出度。事实上PageRank是过渡的马尔科夫矩阵M的主特征向量值，如公式6-4所示，且通常是由任意的向量反复乘以矩阵M确定，直到所得到的矢量的所有项都稳定为止。(www.xing528.com)

原始的PageRank算法数学表达中一共包含了两个部分，第一个部分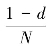中，1-d所表达的是节点链向另一个新的非关联的节点概率，本质上代表了网络中节点发生关联的几率，而这种几率是相同的；而另一个部分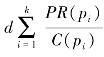实际上是通过权重的分布对结构进行建模。因此，PageRank既考虑了简单的计数，也考虑了网络的结构，但是原始的计算方法并非针对加权网络，因此需要对计算过程进行加权，现有的加权方法很多，但是哪种方法更好并没有定论，本研究中采用Liu和Bollen等人提出的加权算法^[21]，如公式6-6所示：

其中，wij为联系作者的边的权重。由于小世界理论中六度分隔的存在，许多学者会把阻尼系数定在0.85，即有5/6(5/6≈0.85)的几率会顺着当前联系的节点延伸下去，本研究在计算中也遵循这种惯例，阻尼系数定为0.85。由于单个作者的重要性得分和排序结果只是实施聚合过程中的中间阶段，因此正文中不再论述每个作者加权PangRank的得分，相关的结果在附录4中列出。