加入作者的主题模型技术的优化方法

在第5章中，本研究详细论述了如何通过混合概率分布生成资源过程的LDA主题模型，由于LDA模型只是考虑词-主题-文档之间的关联，因此所有的资源的创作者在LDA中都没有被考虑，也就是说LDA将所有的作者等同而视。这种思想就是对作者兴趣建模的基本理念，即在不考虑作者先验下，对于文档中的任意一个词来说，每个作者都是随机的，对词一视同仁地选择使用；词则是通过一个概率分布在词集合中被特定的作者抽取出来。当需要对作者区别对待时，原始的LDA模型就需要进一步的变形，但是，这并不是说LDA主题模型的分析结果有问题，只是模型中考虑的参量进一步增加了，相应的，相关的运算也就更加复杂。

McCallum曾提出了多标签混合建模的思想^[14]，这是一种确定了不同主题分布后的混合加权LDA变形，作者建模的思想就与之类似。但单纯的作者模型中，每个作者相对的主题是固定的，且只对应单个主题，每个主题的混合加权也是固定的。图6-5给出了作者模型的图解释，x表示对于给定的一个词对应的作者，这个作者是以等同几率从作者集合ad中被选择出来，每个作者都对应词集φ中的一个概率分布，这个分布根据Dirichlet先验β确定。对φ的估计能够获得关于作者主题偏好的信息，并且能够用来揭示作者之间的相似性和哪个作者与已知文档的内容更为相关。从图6-5中可以看出，这个模型只是考虑了文档中的词，而没有考虑词所表达的主题语义，且这个模型也没有考虑作者和文档的对应关系。严格来说，这种思想和基于关键词的作者耦合有类似之处，只是增加了概率分布。

作者模型假设每个资源或文档都只对应一个独立的作者，但这种假设明显和事实不符，作者和主题需要在建模中同时考虑。作者主题模型(Author Topic Model，简称ATM)就是在LDA主题模型的基础上对文档内容包含的语义和作者的研究点同时进行建模的方法，最早由Rosen-Zvi等人提出^[15]。在作者模型中，作者创作一个文档d，对于文档中的每个词来说，作者都是一视同仁地使用的；类似于LDA主题模型，作者主题模型中主题的选取是依赖于特定的作者在主题集中的分布，词则通过在主题上的分布生成。

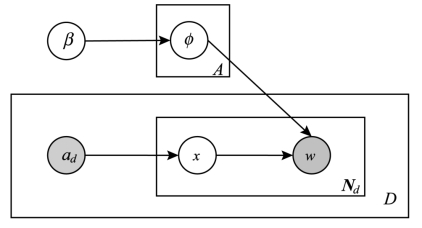
图6-5　作者模型(Author Model)的图表示

定义一个文档d表示为一系列词Nd的向量wd，每个向量wid都是从词的集合V中产生。向量Ad对应数量规模为A的作者集合ad，文档集D则可以定义作者-词对应的一个集合，即D＝[(w1，a1)，…，(wD，aD )]。与LDA主题模型最大的不同在于，作者主题模型加入了作者的先验，其处理文档的生成过程如图6-6所示。

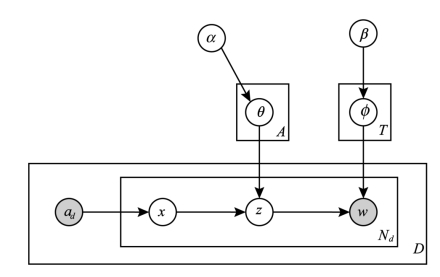
图6-6　作者-主题模型(Author Topic Model)的图表示

图6-6中，φ是词-文档的概率分布，x是作者-词的概率分布，而θ是作者-主题的概率分布，已知的信息有两个，即作者集ad和词w。α和β是两个狄利克雷分布，分别是φ和θ的共轭先验，是整个生成模型的两个参数，其过程可以表述为：(www.xing528.com)

①首先获取作者集ad和词w的对应x；

②假设文档集共包含了A个作者，从Dirichlet先验α中为每个作者抽取多项式分布θ，进行了A次，结果为A个作者-主题分布；

③参照x，从作者-主题分布θ中抽取主题，记为z；

④假设文档集共包含了T个主题，从Dirichlet先验分布β为每个主题抽取多项式分布φ，进行了T次，结果为T个主题-词分布；

⑤依据主题z从主题-词分布中抽取词w。

作者主题模型中，文档集总体上的主题数量T也是由用户所设定的。首先根据α生成作者的主题，然后根据作者和词的对应x生成主题，根据每个词在主题和作者固定的情况下生成最后的词。对于作者集合中的A个作者，对应有A个独立的Dirichlet-Multinomial结构；对于T个主题，也存在T个Dirichlet-Multinomial结构与之对应，即：

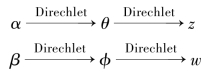
在这个模型中，通过估计参数θ和φ，可以知道作者的研究是哪些主题，并以此分析作者研究的相似性，同时也能进一步揭示每个文档对应了哪些主题。参数θ和φ的估计一般采用吉布斯(Gibbs)抽样来实现^[16]。