LDA主题模型解析及优化探讨

LDA主题模型最初由普林斯顿大学计算机系教授David Blei提出，但其早期思想则可以追溯到Nigam的Mixture of Model模型^[20]和Hofmannt的PLSA(Probabilistic Latent Semantic Analysis，概率潜在语义分析)模型^[21]。LDA是在PLSA的基础上发展而来，采取与PLSA类似的生成式模型，在某种程度上可以视为贝叶斯先验版本的PLSA^[22]。

假设D为包含n篇文档的文档集，则有D＝(d1，d2，…，di，…，dn)，其中di为文档集中第i篇文档。基本的LDA模型将文档表述为词袋，假设词汇之间是可交换的，不考虑句法等因素。具体的，文档di是一个长度为m的词汇序列，即di＝(w1，w2，…，wj，…，wm )，wj表示词汇序列中的第j个词，可以预先设定文档集共包括k个主题。

文档中词汇的分布实际上是多项式分布，从概率的角度来看，直接进行参数估计在获得概率过程中并不现实，因此，可以为多项式分布加上一个先验。在这种情况下，多项式分布的共轭先验Dirichlet(狄利克雷分布)分布是一个很好的选择，这样的选择也方便了后续的计算。此外，生成过程还需要为主题和词汇对应的生成过程确定一个先验，同样的共轭的Dirichlet分布再次被选择，相对于PLSA而言，共轭结构的存在以及先验知识的加入是LDA模型的关键。

图5-3是LDA生成式模型的图表达，展示了通过潜在主题的混合生成目标文档的过程。图5-3中，θ是文档和主题对应的概率分布，β是主题和词对应的概率分布，α和η是两个Dirichlet分布，分别是θ和β的共轭先验，构成生成模型的两个主要参数。文档集的生成过程可以描述为：

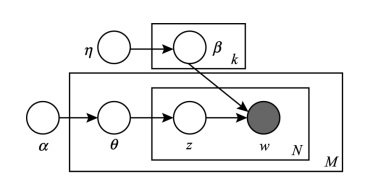
图5-3　LDA主题模型的图表达

①从Dirichlet分布η中抽取每个主题的多项式分布β，由于有k个主题，因此进行k次，结果为k个主题-词分布；

②从Dirichlet分布α中为每个文档抽取多项式分布θ，共进行M次，结果为M个文档-词分布；(www.xing528.com)

③对于每个文档中的每个词，依据上述的结果，首先从文档-词分布θ中抽取主题，记作z；进而从主题-词分布β中抽取词汇w。

通过上述过程可以发现，LDA主题模型实际上是文档生成的一个逆过程，虽然文档集所包含的k个主题是人工设定的，但一个合适的数目并不会对主题建模带来过大的负面影响，通过合适的数值选取，主题抽取的结果可以取得较为理想的效果。

在生成过程中，首先根据α生成词的主题，然后在主题固定的情况下生成词。对于文档集合中包含的M篇文档，存在M个独立的Dirichlet-Multinomial结构与之对应，也存在k个Dirichlet-Multinomial结构对应于k个主题，即：

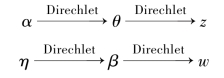
此外，由于LDA主题模型中词的排列方式并未纳入，因此，可以将所有同一主题的词汇抽取，然后形成伪文档，向量表达如下所示：

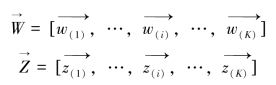
其中，表示第i个主题生成的所有词汇的向量，表示词对应的主题，这样也可以获得文档到主题的分布。要估计LDA模型的参数，期望最大化算法(Expectation-maximization algorithm)和吉布斯(Gibbs)抽样^[23]是两种常用的方法，本研究中主要使用吉布斯抽样。