猴子打字无限次: 打出任何文章

无限猴子定理的意思是，一只猴子随机在英文打字机键盘上按键，在无穷久的时间之后打出《红楼梦》（英文版）的概率为100%.事实上这只猴子还能完整打出国家图书馆里的每一本藏书（全部译为英文）及有史以来人类说过的每一句话（英文译文）.

一般地，无限猴子定理可叙述为有无限只猴子用无限的时间会产生特定的文章.

其实不必出现上述两种无限的事物，一只猴子打字无限次已经足够打出任何文章，而无限只猴子则能即时产生所有可能的文章.

事实上，在无穷长的时间后，即使是随机打字的猴子也可以打出一些有意义的单词，比如，monkey，dog.因此，可以类推，会有一个足够幸运的猴子或连续或不连续地打出一本书，即使其概率比连续抓到一万次同花顺还要低.但在足够长的时间后，其发生是必然的.

大家知道，独立事件同时发生的概率等于其中每个事件单独发生的概率的积.

若一个打字机有50个键，想要打出的词是“monkey”.随机打字时，打出第一个字母“m”的概率是打出第二个字母“o”的概率也是因为事件是独立的，所以连续打出“monkey”的概率是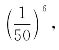同理，接下来继续打出“monkey”的概率也是

所以，在第一段没有打出“monkey”的概率是依然根据独立性原理，连续n段都没有打出“monkey”的概率是(www.xing528.com)

随着n变大，Xn在变小.当n等于100万时，Xn大约是0.9999（没有打出“monkey”的概率是99.99%）；但是当n等于100亿时Xn大约是0.53（没有打出“monkey”的概率是53%）；当n等于1000亿时Xn大约是0.0017（没有打出“monkey”概率是0.17%）；当n趋于无穷时，Xn趋于零.这就是说，只要使n足够大，Xn可以变得足够小.

同样的论证也可以说明在无限多的猴子中有至少一个会打出一段特定的文章.这里Xn其中Xn表示在前n个猴子中没有一个一次打出“monkey”的概率.当我们有1000亿只猴子时，这个概率降低到0.17%，并且随着猴子数量n趋于无穷大，没有打出“monkey”的概率Xn趋于0.

但是，在只有有限的时间和有限只猴子时，就不那么“美好“了！

可观测宇宙中的基本粒子数大约1080，哪怕拥有和这些粒子数同样多的猴子，每只猴子1秒打1000个字母，持续打等同于宇宙的生命长度的时间（大约1018秒），有猴子能幸运打出一本薄书的概率也接近于0.

2003年，一家英国动物园的科学家们“试验”了无限猴子定理，他们把一台电脑和一个键盘放进灵长类园区.可惜的是，猴子们并没有打出什么有意义的只言片语.只打出了5页几乎完全是字母“s”的纸.