斐波那契数列的应用：解决楼梯上升问题

引例：如图1-5-1，蜜蜂家在8号房间，它从1号或2号房间进入，途经其他若干房间回家，如果蜜蜂在任何房间里只能进入相邻房间，且只能从小号房间进入大号房间，则蜜蜂回家的不同路径共有多少种？

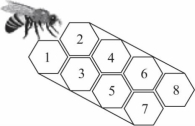
图1-5-1

通过画如图1-5-2所示的树形图列举可以得到答案是34种，这显然是比较烦琐的方法.

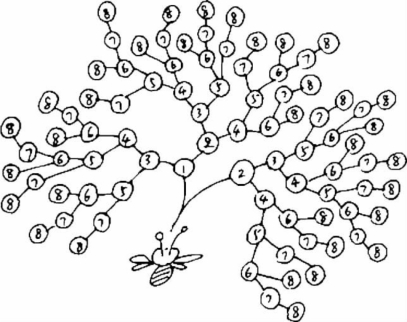
图1-5-2

我们尝试着把问题一般化，设蜜蜂家住n号房，它回家的方法数是an.

蜜蜂回家可分为两类方法，一类是蜜蜂从1号房回家，后面还有n-1个房间，可以有an-1种方法回家；二类是蜜蜂从2号房回家，后面有n-2个房间，可以有an-2种回家方法.

根据加法原理，回家的总方法数是an＝an-1＋an-2，从而蜜蜂到达第n号房的方法数满足an＝an-1＋an-2，且a1＝1，a2＝2，所以易得a8＝34.

本题的递推公式所得数列实际上就是斐波那契数列（只是斐波那契数列中起始两项是1，1这里是1，2），意大利著名数学家斐波那契在他的《算盘书》——被誉为数学史上的一个里程碑——中研究了这个数列，是由研究兔子繁殖问题引出的，所以斐波那契数列也称兔子数列.

斐波那契（意1175—1250）

获得斐波那契数列的通项公式有很多方法，下面我们给出一种.

斐波那契数列：1，1，2，3，5，8，13，21，34，55，…的递推公式为a1＝1，a2＝1，an＋2＝an＋1＋an，n∈N＊.

由a1＝1，a2＝1，an＝an-1＋an-2，n∈N＊，n≥3.

令an-ran-1＝s（an-1-ran-2），n≥3，

则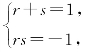

从而an-ran-1＝sn-2（a2-ra1），(www.xing528.com)

所以an＝sn-1＋ran-1，

所以an＝sn-1＋ran-1＝sn-1＋rsn-2＋r2an-2＝…

＝sn-1＋rsn-2＋r2sn-3＋…＋rn-2s＋rn-1.

这是公比为的等比数列前n项和，所以

由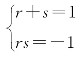解得一组解

代入得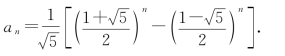

有趣的是，这样一个完全是自然数的数列，通项公式居然是用无理数来表达的.

如果利用这个公式求前一个问题中蜜蜂回家的方法数，则n应取9，即a9＝…＝34.

斐波那契数列“隐身”于大量其他问题之中，比如我们再看下面的问题.

上楼梯的时候，每一步只能跨一级或两级，则登上一个10级楼梯的不同方法数有多少种？

我们依然把问题一般化，寻求递推关系.

设楼梯共有n级台阶，登上这个楼梯的方法数是an.

我们来研究：某人一步可以跨楼梯一级或两级，讨论他登上n级楼梯的方法数.

登上楼梯可分为两类方法，一类是第一步走一级楼梯，还余下n-1级楼梯，则有an-1种方法登到顶端；二类是第一步走两级楼梯，还余下n-2级楼梯，则有an-2种方法登上顶端.根据加法原理，到达楼梯顶的总方法数是

an＝an-1＋an-2，且a1＝1，a2＝2.

当然有a10＝89.

推广的斐波那契数列：改变前两顶，前两项可以是1，3，这样就是1，3，4，7，11，18，…称之为卢卡斯数列.