自然数平方幂的倒数和及优化

自然数平方幂的倒数和问题最早出现于17世纪意大利数学家蒙哥利（1626—1686）的《算术求和新法》，是书中所论求和问题的一个特殊情形.1689年，瑞士著名数学家雅各布·伯努利（1654—1705）发表的论文“具有无限和的无穷级数的算术命题”中部分重复了蒙哥利的无穷级数工作，在论文最后，伯努利称，尽管级数的求和问题易如反掌，但奇怪的是却难以求出.他说：“如果有谁解决了这个迄今让我们束手无策的难题，并告诉我们，我们将十分感激他.”

实际上，当时欧洲的一流数学家，如约翰·伯努利及其子丹尼尔·伯努利（1700—1782）、哥德巴赫、莱布尼茨、棣莫弗（1667—1754）、斯特林（1692—1770）等都未能解决这一难题，其中哥德巴赫在与丹尼尔的通信（1729）中给出和的上、下限1.644和1.645；斯林特在其《微积分》（Methodus differentialis，1730）中给出近似值1.64493466.

瑞士大数学家欧拉最早于1735年解决了这个所谓“巴塞尔难题”，这是他年轻时期最著名的成果之一.以后欧拉又陆续获得不同的解法.

欧拉的方法涉及高等数学的级数展开问题，这里不作介绍，以下是一个初等方法，出自艾格纳和齐格勒所著Proofs from THE BOOK.

考虑2n＋1次单位根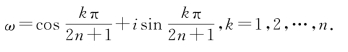

令则cosxk＞0，sinxk＞0，k＝1，2，…，n.

那么，根据单位根的定义，有

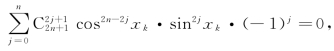根据复数相等的条件，虚部为0，即两边约去一个sinxk，得亦即(www.xing528.com)

两边同除以sin2nxk，得

这表示cot2xk（k＝1，2，…，n）是方程（-1）n＝0的n个根.

根据韦达定理有

从而

由于在上有sinx＜x＜tanx，故有因此

这就是

即对n→∞取极限，再利用夹逼定理，即得