直到欧拉之前，研究三角函数大都在一个确定半径的圆内进行的.如古希腊的托勒密定半径为60；印度人阿耶波多（约476—550）定半径为3438；德国数学家里基奥蒙特纳斯（1436—1476）为了精密地计算三角函数值曾定半径为600000；后来为制订更精密的正弦表又定半径为107.因此，当时的三角函数实际上是定圆内的一些线段的长.
过去一般称AB为
的正弦，把正弦与圆牢牢地连接在一起（如图1-4-1），意大利数学家利提克斯（1514—1574）改变了前人的做法，把它称为∠AOB的正弦，从而使正弦值直接与角挂钩，而使圆O成为从属.
欧拉在《无穷小分析引论》一书中首次令圆的半径为1，即置角于单位圆之中，从而定义三角函数为相应的线段与圆半径之比.
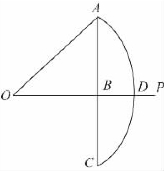
图1-4-1
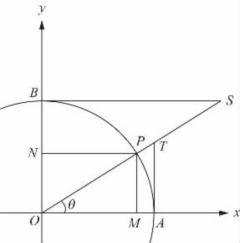
图1-4-2
（1）正弦（sine）
（2）余弦（cosine）
（3）正切（tangent）
(www.xing528.com)
（4）余切（cotangent）
（5）正割（secant）
（6）余割（cosecant）
（7）正矢（versine）
（8）余矢（versed cosine）
（9）外割（exsecant）
图1-4-2称为三角圆（半径＝1），是用图形的方式表达各函数.其中我们可以看到，sinθ为PM线段，也就是圆中一条弦（对2θ圆周角）的一半，所以称为“正弦”.而cosθ是OM线段，但OM＝NP，故我们也可以将cosθ视为∠NOP（90°-θ）的正弦值，也就是θ的余角的正弦值，故称之为“余弦”.其余类推.
事实上，在历史上曾出现过的三角函数种类超过十种，除了上面列举的，其他的还有如半正矢（havθ）、古德曼函数和反古德曼函数等.
三角函数传入中国时，正、余矢函数还未废弃，故徐光启将八种三角函数称为“八线”.后来因为矢类函数废弃不用，故八线之名渐被“三角”取代，统一的名称到了民国以后才确立.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
