韦达定理说明了一元二次方程中根和系数之间的关系.
弗朗索瓦·韦达1615年在著作《论方程的识别与订正》中建立了方程根与系数的关系，提出了这条定理.由于韦达最早发现代数方程的根与系数之间有这种关系，人们把这个关系称为韦达定理.
韦达（法1540—1603）
韦达定理：在一元二次方程ax2＋bx＋c＝0（a，b，c∈R，a≠0）中，两根x1，x2有如下关系
证明：事实上，ax2＋bx＋c＝a（x-x1）（x-x2）＝ax2-a（x1＋x2）x＋ax1x2，所以由对应系数相等得
无论方程有无实数根，实系数一元二次方程的根与系数之间适合韦达定理.
韦达定理逆定理：如果两数α和β满足如下关系
那么这两个数α和β是方程ax2＋bx＋c＝0（a，b，c∈R，a≠0）的根.
通过韦达定理的逆定理，可以利用两数的和积关系构造一元二次方程.
韦达定理不仅可以说明一元二次方程根与系数的关系，还可以推广说明一元三次、一元n次方程根与系数的关系.
设一元三次方程ax3＋bx2＋cx＋d＝0，a≠0，x1，x2，x3是其三个根，则有
事实上，据假设有ax3＋bx2＋cx＋d＝a（x-x1）（x-x2）（x-x3）
＝ax3-a（x1＋x2＋x3）x2＋a（x1x2＋x2x3＋x3x1）x-x1x2x3
所以由对应系数相等得
同理，设一元n次方程a0xn＋a1xn-1＋a2xn-2＋…＋an＝0，a0≠0，x1，x2，…，xn是其n个根，则有(www.xing528.com)
现在我们来看两个应用的例子.
问题1 已知a，b，c∈R，证明a，b，c为正数的充分必要条件是
必要性显然，考察充分性.
观察命题的条件，可以看到a＋b＋c，ab＋bc＋ca，abc恰好是a，b，c的一次、二次、三次轮换对称式，这就使我们联想到一元三次方程根与系数的关系.
令a＋b＋c＝p，ab＋bc＋ca＝q，abc＝r，则a，b，c为方程f（x）＝x3-px2＋qx-r的三个根.这样，就可以用反证法证明如下：
设a，b，c不全大于零，不失一般性，可以设x＝a≤0，则因为p，q，r＞0，不管是a＜0还是a＝0均可推得
f（a）＝a3-pa2＋qa-r＜0.
这与a是方程f（x）＝0的根矛盾.
所以f（x）＝0的三个根必完全为正数.
问题2 解方程组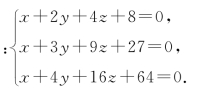
按常规思维，可用加减法或行列式法求解，但计算冗繁.仔细观察发现上述三式形式非常统一即都具有x＋ay＋a2z＋a3＝0（其中a＝2，3，4）的形态，于是可视常数2，3，4为变量的不同取值，构造关于t的三次方程：t3＋t2z＋ty＋x＝0，则t＝2，3，4是方程的根.
从而由一元三次方程根与系数的关系知：
z＝-（2＋3＋4）＝-9；y＝2×3＋4×3＋2×4＝26，x＝-2×3×4＝-24.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
