无限集的元素个数意义及探讨

从古希腊时代起，无限集之谜就一直困扰着哲学家、数学家，直到19世纪，德国数学家康托尔创立了集合论，才揭开了“无限”的面纱.

伽利略（1564—1642）是最伟大的科学家之一，生于意大利的比萨，自称阿基米德的学生.他曾把全体自然数和它们的平方用下面的方式一一对应起来：

它们谁也不多一个，谁也不少一个，就是说应该一样多.可是，自然数的平方明明只是全体自然数的一部分，怎么会和自然数一样多呢？难道部分可以等于全体吗？伽利略百思不得其解.后人就称这个问题为“伽利略悖论”.

康托尔在《一般集合论基础》等文献中，澄清了有关无限集的许多问题，被大家公认为集合论的创建者.他认为“伽利略悖论”不是怪论，而是完全正确的.任何两组东西，只要能够建立元素间的一一对应，就是一样多.与有限集的本质区别是，无限集可以与自己的某真子集建立元素间的一一对应关系.

康托尔通过构造一一对应，证明了有理数的个数与自然数一样多.

他首先把所有正有理数排列成下列形式.

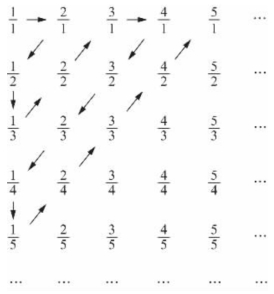
显然，任何正有理数均出现在这个排列中.如果我们按箭头所示的次序排列出这些数1，

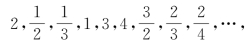中途丢掉之前已经排列上的数，就会得到一个没有尽头的序列r1，r2，r3，…，于是，序列0，-r1，r1，-r2，r2，-r3，r3，…正好是所有有理数的集合，建立如下一一对应：

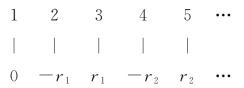
这就证明有理数的个数与正自然数是一样多的.

我们把元素个数与正自然数相等的无穷集合叫作可列集合，也称这样的集合为可数的.

至此，人们更倾向于相信：所有无限集都是可列的，即元素个数都和正自然数一样多，唯一要做的事情仅仅是在两者之间如何建立恰当的一一对应.

然而，康托尔出人意料地证明了即使是［0，1］中的全体实数也是不可列的（意味着有着比正自然数更多的数）.他在1890年的一篇论文中，巧妙地给出了一个证明：

用反证法.假设［0，1］是可列集，那么就可以把其中的数排列成如下的形式：

a1，a2，a3，…，an，…

另外，我们知道在［0，1］区间上的每一个实数都可以表示为唯一的无限小数0.p1p2p3….即使是有限小数也可以唯一地化为无限小数的形式，例如

0.6＝0.59999…，0.88＝0.87999…，1＝0.99999…，0＝0.00000…，(www.xing528.com)

因此，

a1＝0.p11p12p13…p1n…；

a2＝0.p21p22p23…p2n…；

a3＝0.p31p32p33…p3n…；

…

an＝0.pn1pn2pn3…pnn…；

…

康托尔用对角线法构造了一个无限小数

q＝0.q1q2q3…qn….

他选取q1≠p11，q2≠p22，…，qn≠pnn，….那么这个数显然在区间［0，1］上，但与任一个ai都不同，这就出现了矛盾.所以区间［0，1］上的实数是不可列的，这就意味着区间［0，1］上的实数个数比自然数或有理数要多.

如图1-1-1，取一个长度为1的半圆（不含端点），O是其圆心，显然半圆上的点与（0，1）上的实数是一一对应的，而直线上的点与整个实数集中的实数是一一对应的，按该图方式就构造了一个半圆上的点与整个直线上的点的一一对应关系.说明（0，1）上的实数个数与整个实数集上的实数个数一样多.

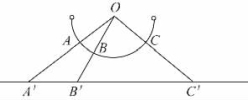
图1-1-1

根据以上结论，全体实数是不可列的.所以推得无理数集是不可列的，说明无理数比有理数多！

如果记集合A的元素个数为CardA，事实上

Card｛奇数｝＝Card｛偶数｝＝Card N＊＝Card N＝Card Z＝Card Q

＜Card（0，1）＝Card R

将有理数“个数”记为Card Q，实数“个数”记为Card R，那么是否存在一种集合X，它的元素“个数”Card X大于Card Q而小于Card R呢？这就是著名的康托尔“连续统假设问题”.该问题吸引了众多数学家的兴趣，至今尚未彻底解决.