【摘要】：法国大数学家费马提出其“小定理”时，虽然声称他是有证明的，但他没有把证明写在后人可见之处，第一个公开发表的证明是欧拉给出的，而这几乎是100年后的事情了.费马（法1601—1665）费马小定理：设p是素数，n是任何整数，则np-n被p整除.证明：首先对正整数n，用数学归纳法证明定理是成立的.当n＝1时，np-n＝1p-1＝0，被p整除；设当n＝m时，命题成立，即np-n＝mp-m被p整除，则当n＝
法国大数学家费马提出其“小定理”时，虽然声称他是有证明的，但他没有把证明写在后人可见之处，第一个公开发表的证明是欧拉给出的，而这几乎是100年后的事情了.
费马（法1601—1665）
费马小定理：设p是素数，n是任何整数，则np-n被p整除.
证明：首先对正整数n，用数学归纳法证明定理是成立的.
当n＝1时，np-n＝1p-1＝0，被p整除；
设当n＝m时，命题成立，即np-n＝mp-m被p整除，则当n＝m＋1时，
由于
是整数，故分母是分子的约数.但分母的各个因数都小于素数p，因而都不可能是p的约数，所以整数
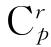必含有因数p，可以被p整除.这样一来，①式右边中的第二个括号内的数被p整除，根据归纳假设，第一个括号内的数也被p整除，所以np-n被p整除.于是，当n＝m＋1时命题也成立.(www.xing528.com)
所以，对正整数n，np-n被p整除.
其次，设n是负整数.
若素数p＝2，则n2-n＝n（n-1）是两个连续自然数的积，必为偶数，当然被p＝2整除；
若p为奇素数，则np-n＝-（-n）p＋（-n）＝-［（-n）p-（-n）］，由于-n是正整数，故由第一阶段的证明，（-n）p-（-n）被p整除，从而np-n被p整除.
总之，对一切整数n，np-n被p整除.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
