精确估计面板数据的软件操作 - 使用GMM方法估计面板数据的步骤

1．GMM软件估计操作

（1）在对面板数据进行GMM估计时，workfile必须是面板结构的条件下进行。假定模型被设为动态模型，利用Eviews估计动态面板数据模型时，则打开workfile窗口后，在主菜单选择Object/new object/Equation，或者Quick/Estimatie Equation，打开面板数据估计设定对话框，在Method选择GMM/DPD-Generalized Method of Moments/Dynamic Panel Data，对话框就增加了一个Instrument页面，如图16-1所示。

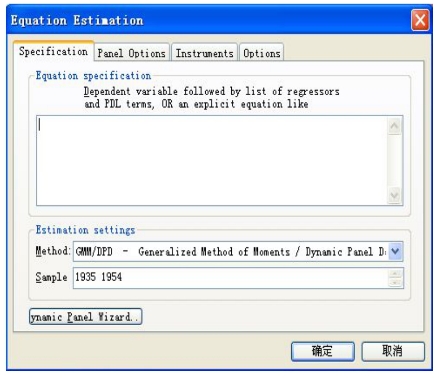
图16-1　面板数据估计设定对话框

（2）点击Dynamic Panel Wizard帮助填写上面的Equation Estimation，首先是一个描述介绍Wizard的基本目的。然后点击“Next”，到图16-2所示的页面。

图16-2　点击“Next”得到的页面

在这个页面要写下因变量以及因变量作为解释变量的滞后阶数，一般应选择2。

（3）点击“下一步”，到了另一个页面（见图16-3），在这个页面中设定公式中剩下的解释变量，比如：本例除了I（-1），另外的解释变量是F和K，在该页面填入F和K。

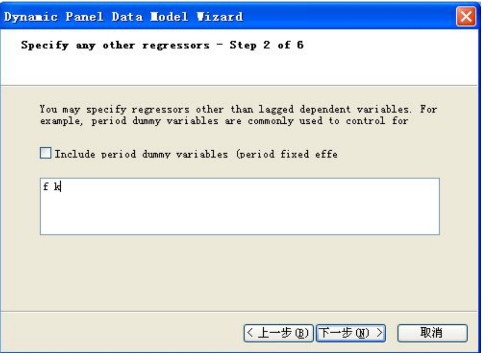
图16-3　点击“下一步”得到的页面

如果设定是时点固定影响动态面板数据模型则可以在Include period dummy variables复选框打钩，然后点击下一步。

（4）该页面（见图16-4）设定消去截面固定效应的转换方式，可以选择Difference或者Orthogonal deviations，Eviews默认的是前者。

图16-4　设定消去截面固定效应的转换方式页面

（5）点击“下一步”。在这个页面（见图16-5）里Eviews预先默认地因变量的滞后项一项为工具变量，可以在这里设置@DYN（I，-2，-3，-4），则需要的三个工具变量都已设定好，则下个页面不用加其他的工具变量，如果只是@DYN（I，-2）一个工具变量，则在后面还要设定工具变量。

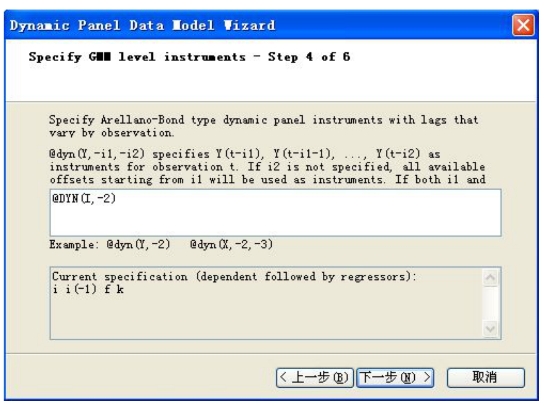
图16-5　EViews默认因变量的滞后项为工具变量

比如这里用F和K的滞后项作为工具变量，在页面（见图16-6）中填入Transform（differences），如果前面没有选择Differences，则要将工具变量填入No transformation。

图16-6　在页面中填入Transform（differences）

（6）点击“下一步”到了设定GMM加权和系数协方差计算方法的页面（见图16-7），Eviews提供了三种计算方法，假定选择两步广义矩估计，另外还提供了设定标准方差的计算方式，Period SUR和White period。

图16-7　设定GMM加权和系数协方差计算方法页面

点击“下一步”后，出现了一个完成的对话框，点击“完成”后，就回到最初估计设定对话框中，如图16-8所示。

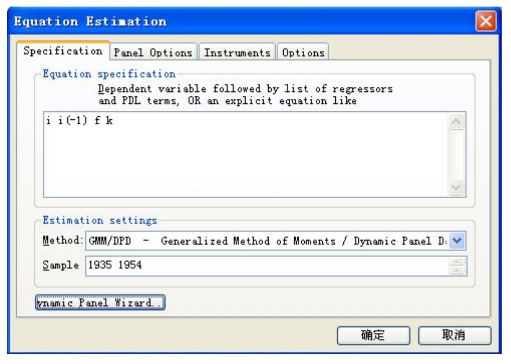
图16-8　最初估计设定对话框页面

在该对话框中将刚才为动态面板数据模型进行估计的设定已经填入了Equation Estimation，可以点击Specification、Panel Options、Instruments和Options进行核实，然后点击“确定”，得到动态面板数据估计的结果，如图16-9所示。

图16-9　动态面板数据估计的结果

2．单位根检验操作

EViews软件都提供了以上的六种检验方法。

（1）在pool对象中进行单位根检验。

首先在打开pool或者单独一个面板数据结构的序列的窗口中，选择View/Unit Root Test，打开如图16-10所示的对话框。

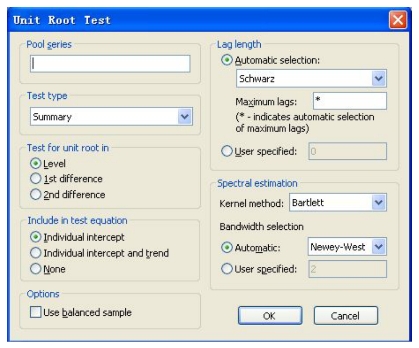
图16-10　选择View/Unit Root Test对话框

在pool series填入要检验序列，比如“i？”，然后在Test type里选择单位根检验的方法本例选LLC方法，如图16-11所示。

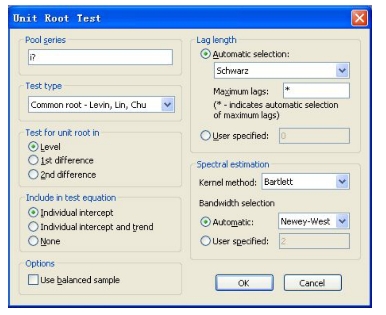
图16-11　LLC方法

其他设定与时间序列单位检验类似，其他都默认Eviews设定后点击“OK”，得到对于变量I的单位根检验结果，如图16-12所示。

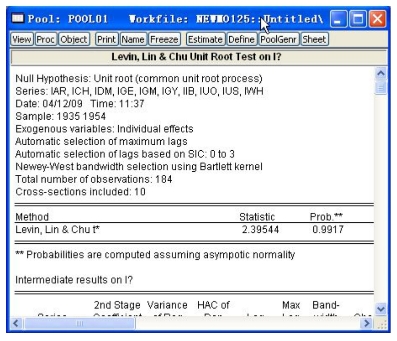
图16-12　对于变量I的单位根检验结果

对于变量I，LLC检验的原假设是有单位根的假设，从统计量的值以及p值（见图16-13），可以看出不能拒绝原假设，接受有单位根的假设，说明面板数据序列I是非平稳的。如果需要还可以继续进行一阶差分和二阶差分下的单位根检验。

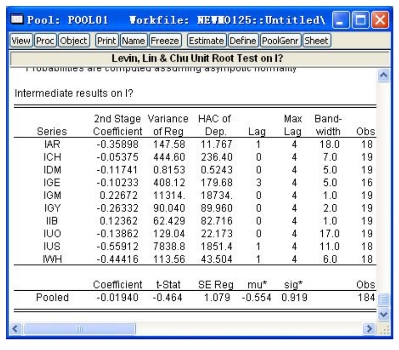
图16-13　统计量的值以及p值

另外，LLC检验结果还包括了每个截面的自回归系数，回归方差，因变量的HAC，最大滞后阶数等等。

（2）在面板结构序列中进行单位根检验。

除了可以在pool对象中对某变量的序列进行单位根检验外，还可以在面板结构的workfile中进行单位根检验。

①在面板结构的workfile中打开I序列，然后点击View/Unit Root Test，打开单位根检验的设定窗口，操作如图16-14所示。

图16-14　单位根检验的设定窗口

②选择LLC单位根检验的方法，其他均保持Eviews默认的设定，如图16-15所示。

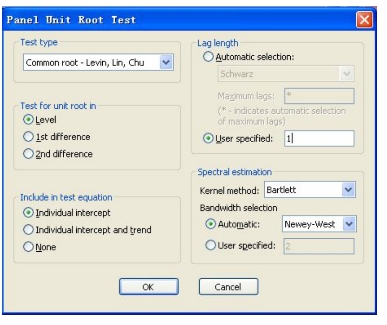
图16-15　LLC单位根检验的方法

③点击OK后，得到检验结果（见图16-16），与在pool中检验的结果一样，除了显示了LLC检验统计量的值以及每个截面的自回归系数等等。

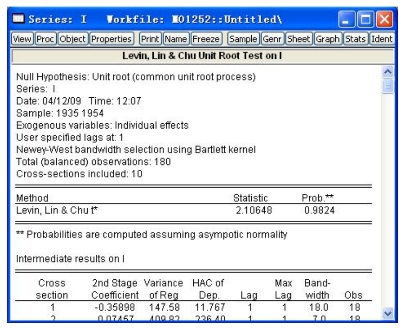
图16-16　检验结果窗口

因为I序列在水平值不平稳，再进行一阶差分序列检验，结果如图16-17所示。

图16-17　一阶差分序列检验

结果显示拒绝了原假设，则一阶差分是平稳。

④若是对序列“i？”进行Hadri单位根检验，原假设是不存在单位根，我们可以得到如图16-18所示的结果。

图16-18　Hadri单位根检验

从检验结果中可以看出，Hadri的z统计量和Heteroscedastic一致z统计量都表明拒绝原假设，即该序列“i？”存在单位根。

3．协整检验软件操作

面板数据协整检验在pool对象和面板结构文件夹中都可以做。Eviews提供上面介绍的三种检验方式进行面板协整检验。由于前面单位检验I，F和K序列的一阶差分是平稳的，则可以对原序列进行协整检验。

（1）在workfile面板数据结构中，打开I，F和K群窗口，然后点击群窗口菜单上的Views/Cointegration Test，可以进行类似时间序列协整检验的相关的设定，但由于面板数据的特殊性，选Test type一种类型，相应的Deterministic trend specification也不一样。例如首先选择Pedroni检验方法，则设定窗口如图16-19所示。

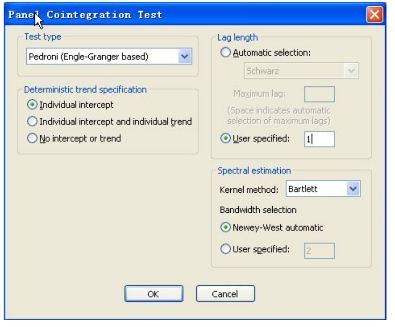
图16-19　Pedroni检验方法设定窗口

Deterministic trend specification设定时，如果想包含个体固定效应或截距，则可以选择Individual intercept；若想包含个体和时期固定效应，则可以选择Individual intercept and individual trend；或者两种都没有选No intercept or trend。(www.xing528.com)

估计结果如图16-20所示。

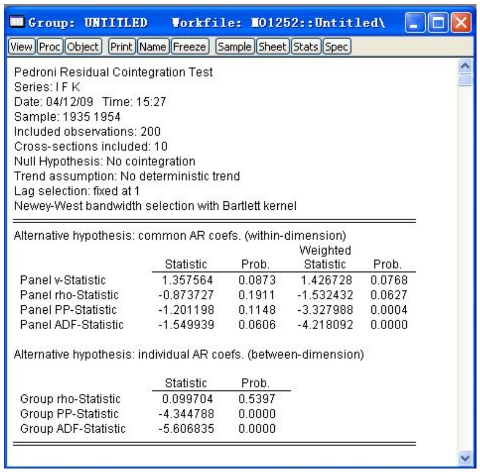
图16-20　估计结果

检验结果的顶部显示了检验方法，原假设，外生变量设定以及其他相关的检验设置。下面接着是Pedroni检验的几个相关统计量，用于拒绝同质性和异质性的相关假定。检验结果的上半部分是同质性假定的检验结果，即假定所有截面有共同的AR系数，EViews给出了相应的统计量加权与未加权时的取值及其相伴概率。可以看出Panel v统计量和Panel rho统计量在显著性水平10%时拒绝没有协整的零假设，而Panel PP统计量和Panel ADF统计量在1%显著性水平拒绝了零假设，认为所有截面有共同的AR系数，且该系数的值小于1。接下来，给出了异质性假设的检验结果，即只要求每个截面的AR系数值小于1，也给出了相关的统计量取值和相伴概率，从上面的结果可以看出Group rho统计量不能拒绝原假设，即认为不存在协整关系，而Group PP统计量和Group ADF统计量均很显著，拒绝原假设，认为存在异质性协整关系。

结果还显示了在计算统计量中间使用的辅助回归结果（见图16-21），因为Pedroni检验是分为两部分的，第一部分包含Phillips-Peron非参数结果，第二部分是扩展的Dickey-Fuller参数结果。

图16-21　辅助回归结果

若选择Kao检验，则窗口变成如图16-22所示的形式，并且只能设定个体固定效应或个体截距，如下图：

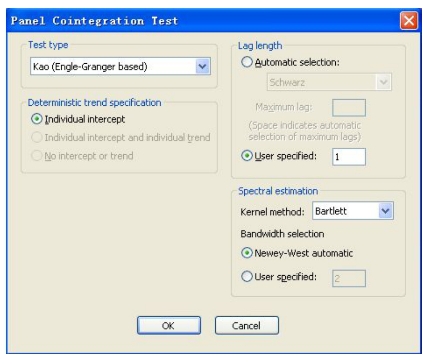
图16-22　选择Kao检验的窗口

检验结果类似与Pedroni检验（见图16-23），可以看到ADF统计量的值和prob拒绝值，证明了拒绝原假设，即该三个变量之间存在协整关系。

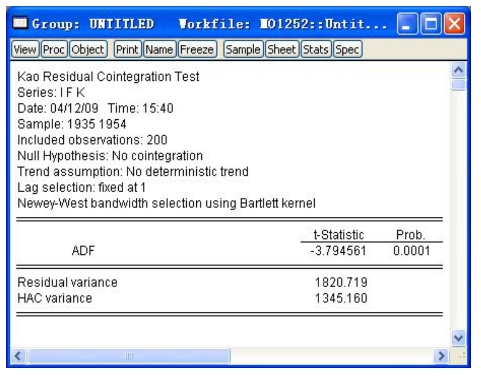
图16-23　检验结果

该检验也是对残差进行混合辅助回归，但每个截面的残差回归方程一样，因此在图16-24中看出残差的滞后项和滞后项的差分系数都是显著的。

图16-24　对残差进行混合辅助回归

还可以选择Fisher检验，该检验与Johansen类似，设定窗口也一样，如图16-25所示。

图16-25　Fisher检验设定窗口

结果显示也与Johansen显示一样（见图16-26），具体的分析可以参见时间序列协整分析。

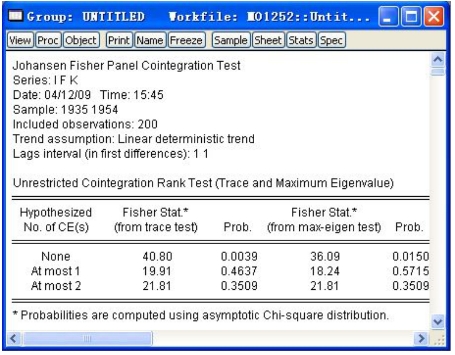
图16-26　检验结果

（2）另外可以在pool对象中进行协整检验，同样在pool窗口菜单中点击Views/Cointegration Test，这时窗口多了一个设定序列的窗口，在左上面的Variables处填入至少两个序列进行协整检验，其他的设定与面板结构中的一样，检验结果也类似。

4.面板Granger因果检验

在经济分析中，往往要研究两经济变量间的因果关系。例如，在研究金融发展与经济增长的关系时，是金融发展促进了经济增长，还是经济增长带动了金融发展，或者二者互为因果。但由于不同的经济理论所依据的前提假设不一致，使得单凭经济理论很难作出合理的判断。

Granger因果检验的具体思想参见前面的时间序列因果检验思想，但传统的Granger因果检验在单个经济体经济变量的因果关系检验中发挥了重要的作用，当面对具有时间和个体双重维度的数据（面板数据）时有些束手无策。近年来，国外很多学者对面板数据下Granger因果检验的理论和应用进行了很多的研究，取得了一定的成果。国外现有的面板数据的因果检验方法都是基于传统的Granger因果检验的思想，将其推广到面板数据的情形。构造如下的VAR模型（时间平稳的），计算受约束的回归RSSr和无约束回归的RSSu，然后构造Wald统计量对βi的线性约束进行检验。

在Eviews软件操作也与时间序列类似，打开整个群组序列，然后在群组窗口工具栏中，点击view/Granger Causality，如图16-27所示。

图16-27　点击View/Granger Causality得到的窗口

从上面结果中可以看出F不是I的Granger原因，I也不是F的Granger原因；而1%的显著性水平下认为K是I的Granger原因，I也是K的Granger原因。

【案例】

根据《中国统计年鉴》数据，2008—2013年中国东北、华北、华东15个省级地区的城镇居民家庭人均消费（cp，不变价格）和人均可支配收入（ip，不变价格）及消费者物价指数如表16-1、16-2、16-3所列。

表16-1　2008—2013年中国东北、华北、华东15个省级地区的城镇居民人均消费　单位：元

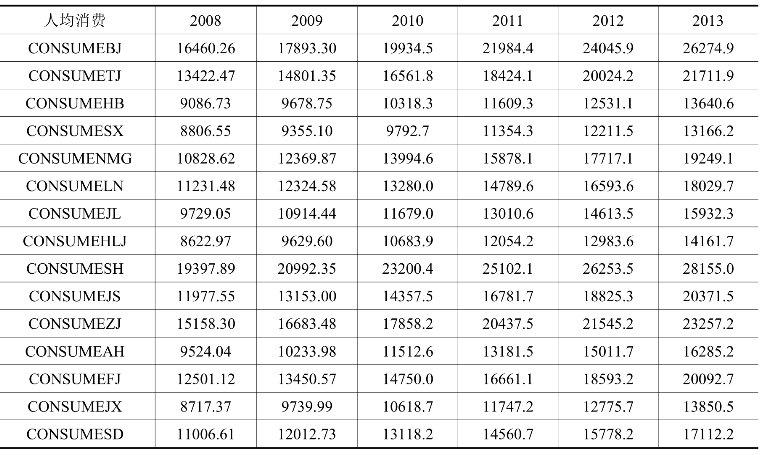
表16-2　2008—2013年中国东北、华北、华东15个省级地区的城镇居民人均可支配收入　单位：元

表16-3　2008～2013年中国东北、华北、华东15个省级地区的城镇消费者物价指数

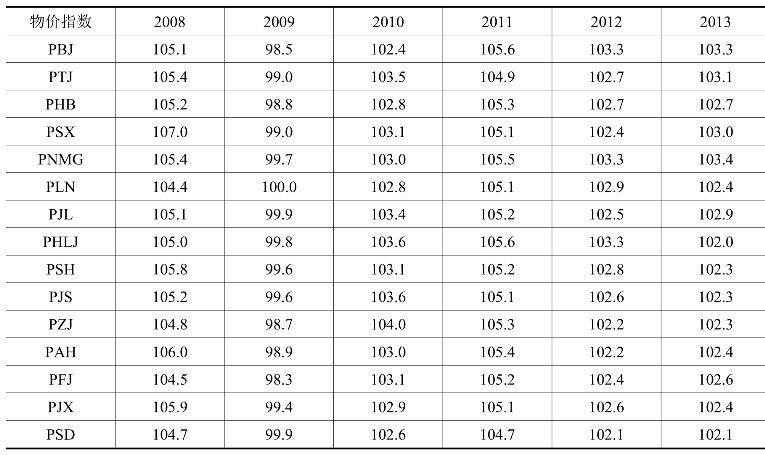
定义

（1）建立面板数据（Panel Data）工作文件。

首先建立工作文件。打开工作文件窗口，点击主功能菜单上的Objects键，选New Object功能，从而打开New Object（新对象）选择窗。在Type of Object选择区选择Pool（合并数据库），并在Name of Object选择区为合并数据库起名Consume（初始显示为Untitled）（见图16-28）。点击“OK”键，从而打开合并数据库（Pool）窗口。在窗口中输入15个不同省级地区的标识BJ（北京）、TJ（天津）、HB（河北）、SX（山西）、NMG（内蒙古）、LN（辽宁）、JL（吉林）、HLJ（黑龙江）、SH（上海）、JS（江苏）、ZJ（浙江）、AH（安徽）、FJ（福建）、JX（江西）、SD（山东），如图16-29所示。

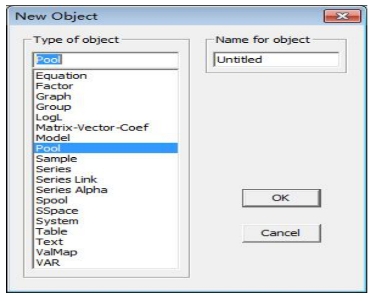
图16-28　合并数据库Consume窗口

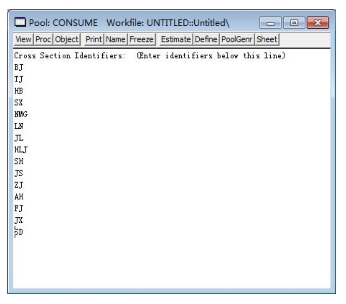
图16-29　合并数据库Pool窗口

（2）定义序列名并输入数据。

在新建的Pool（合并数据库）窗口的工具栏点击Sheet键，从而打开Series List（列写序列名）窗口（见图16-30），定义时间序列变量“consume？”“income？”和“p？”。点击OK键，工作文件中会出现3×15个尚未输入数据的变量名。3个变量的后缀分别为AH，BJ，FJ，HB，HLJ，JL，JS，JX，LN，NMG，SD，SH，SX，TJ，ZJ（见图16-31）。点击Pool窗口的Edit＋/－键，使窗口处于可编辑状态，通过键盘输入或粘贴的方法输入数据。

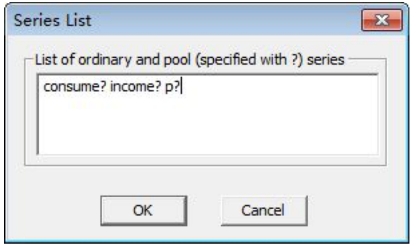
图16-30　Series List（列写序列名）窗口

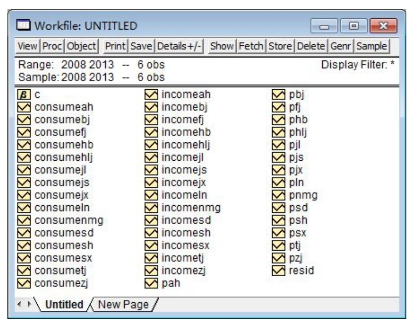
图16-31　数据的变量

也可以在工作文件中选中该45个变量，用Show命令打开数据组（Group）窗口，使窗口处于可编辑状态，然后通过键盘输入或粘贴的方法输入数据。

下面介绍怎样通过PoolGenr键生成新数据。重新打开一个Pool（合并数据库）窗口，在窗口中输入变量后缀（标识），分别为AH，BJ，FJ，HB，HLJ，JL，JS，JX，LN，NMG，SD，SH，SX，TJ，ZJ。点击Pool窗口中的PoolGenr键，在弹出的对话框中输入

点击OK键，就可以同时生成15个cp变量。同理，也可以生成15个ip变量。“cp？”“ip？”分别是固定价格的城镇居民家庭人均消费和人均可支配收入变量。

（3）单位根检验。

在Pool（合并数据库）窗口的工具栏点击View中的“Unit root test”键，从而打开单位根检验窗口，先后输入时间序列变量“cp？”“ip？”，检验原序列是否平稳，如图16-32所示。

图16-32　单位根检验窗口

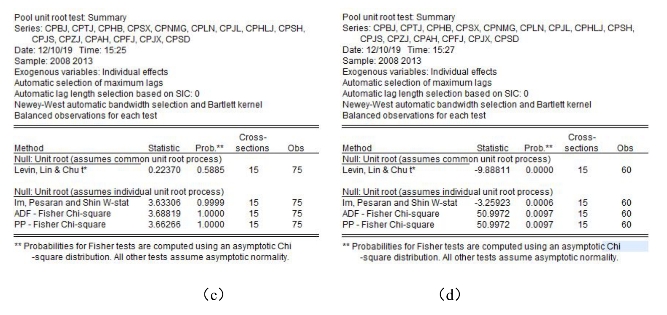
图16-32　单位根检验窗口（续）

由检验结果可以看出，“cp？”“ip？”均属于原序列存在单位根，一阶差分后平稳，可能存在协整关系，进一步利用协整检验进行分析。在Pool（合并数据库）窗口的工具栏点击View中的“Cointegration test”键，从而打开协整检验窗口，输入时间序列变量“cp？”“ip？”，检验是否存在协整关系，如16-33所示。

图16-33　检验cp？和ip？是否存在协整关系

由检验结果可以看出，“cp？”和“ip？”存在协整关系，可以构建面板模型进行分析，但是选择固定效应面板模型还是随机效应面板模型，需要进一步检验。在Pool（合并数据库）窗口的工具栏点击Estimate键，分别输入时间序列变量“cp？”和“ip？”，选择随机效应模型，并进行Hausman test，如图16-34所示。

图16-34　随机效应模型检测

由检验结果可以看出，原假设成立，应该选择随机效应面板模型。同时从参数的估计结果来看，参数估计值C、β均通过了1%的显著性水平检验，说明模型的系数非常显著，并且从模型的拟合度来看，R2为0.97，因此，随机效应面板模型的拟合优度很高，且面板回归方程为：

由方程可以看出，ip的系数为0.58，说明人均收入越高，消费水平也会随之而上升。此外，上海的随机效应值最高，为1415.93，说明上海的人均消费水平要高于其他城市。