动态面板模型原理与单位根检验方法详解

由于经济个体行为的连续性、惯性和偏好等影响，经济行为是一个动态变化过程，这时需要用动态模型来研究经济关系。本章主要讨论动态面板数据模型的一般原理和估计方法，然后介绍了面板数据的单位根检验、协整分析和格朗杰因果检验的相关原理及操作。

1．动态面板模型原理

考虑线性动态面板数据模型为

首先进行差分，消去个体效应得到方程为：

可以用GMM（广义矩估计）对该方程进行估计。方程的有效的GMM估计是为每个时期设定不同数目的工具，这些时期设定的工具相当于一个给定时期不同数目的滞后因变量和预先决定的变量。这样，除了任何严格外生的变量，可以使用相当于滞后因变量和其他预先决定的变量作为时期设定的工具。例如，方程（16-2）中使用因变量的滞后值作为工具变量，假如在原方程中这个变化是独立同分布的，然后在t=3时，第一个时期观察值可作为该设定分析，很显然Yi1是很有效的工具，因为它与ΔYi2相关的，但与εi3Δ不相关。类似地，在t=4时，Yi2和Yi1是潜在的工具变量。以此类推，对所以个体i用因变量的滞后变量，我们可以形成预先的工具变量：

每一个预先决定的变量的相似的工具变量便可以形成了。

假设εit不存在自回归，不同设定的最优的GMM加权矩阵为：

式中：是矩阵，，Zi包含严格外生变量和预先决定的变量的混合。该加权矩阵用于one-step Arellano-Bond估计。

给定了one-step估计的残差后，我们就可以用估计计算的White时期协方差矩阵来代替加权矩阵Hd：

该加权矩阵就是在Arellano-Bond两步估计中用到的矩阵。

我们可以选择两者中一个方法来改变最初的方程，以消除对总体偏离而计算的个体效应。详情见后面的GMM估计，用正交偏离而转换残差有个特点就是转换设定的第一阶段最优加权矩阵是简单的2SLS加权矩阵：

2．动态面板的GMM估计方法

（1）基本的GMM面板估计是基于以下的矩形式：

式中：Zi是每个截面i的Ti×p阶工具变量矩阵，且有

在某些情形总和是做时期上加总的，而不是个体，我们将使用对称矩阵计算。

GMM估计的最小二次式为：

为了估计β，选了合适的p×p阶加权矩阵H。

系数向量β已知时，则可以对系数协方差矩阵进行计算：

这里通过下面式子进行估计：

而

在简单的线性模型中，我们可以得到系数的估计值为：

方差估计为：

式中：MAB一般形式为

与GMM估计相关的有：（1）设定工具变量Z；（2）选择加权矩阵H；（3）决定估计矩阵Λ。

（2）大范围的设定可以被认为是GMM估计中的特例。例如，简单的2SLS估计，是用系数协方差的普通估计，设定：

代入计算，我们可以得到系数相同的表达式：

则方差矩阵为

而有约束和无约束的异方差和同期相关的标准差可以用一个新的表达式计算：

因此我们得到一个white截面系数协方差估计。而协方差方法在前面线性面板数据模型中已经详细介绍了，在此不再叙述。

（3）另外还有其他的GMM协方差计算的可供选项，比如：2SLS，White cross-section，White period，White diagonal，cross-section SUR（3SLS），cross-section weights，Period SUR，Period weighs。另外不同的误差加权矩阵在用GMM估计动态面板数据时可能经常用到。

这些权重的形成已经在前面的线性面板数据方差结构中详细阐述了，例如cross-section SUR（3SLS）加权矩阵的计算方式为：

式中：ΩM是对同期相关协方差矩阵的估计。类似地，White period加权通过下式计算为：

这些后来的GMM加权方式是与干扰项中存在任意序列相关和时间变化协方差相关联的。

（4）GLS设定

Eviews也可以利用GMM设定估计GLS转换的数据，因此条件矩阵就要修订，以反映GLS的权重：

3．面板数据的单位根检验

时间序列的单位根检验问题是现代计量经济学研究的一个焦点问题，长期以来人们发现许多宏观经济序列都呈现明显的非稳定单位根过程的特征。若不对经济变量进行平稳性检验，而直接建模则易于产生伪回归现象。面板数据包括了时间维度和截面维度的数据，时间维度较小时，我们可以用面板数据直接建模，但时间维度增加到一定长度时，则需要对面板数据进行平稳性检验，即单位根检验。

面板数据的单位根检验同普通的单序列的单位根检验方法虽然类似，但两者又不完全相同。本书主要介绍五种用于面板数据的单位根检验的方法。

对于面板数据考虑如下的AR（1）过程：

式中：Xit表示模型中的外生变量向量，包括各个体截面的固定影响和时间趋势。N表示个体截面成员的个数，Ti表示第i个截面成员的观测时期数，参数ρi为自回归的系数，随机误差项uit满足独立同分布的假设。如果，则对应的序列yi为平稳序列；如果，则对应的序列yi为非平稳序列。

4．面板数据单位根检验分类

根据不同的限制，可以将面板数据的单位根分为两类。一类是相同根情形下的单位根检验，这类检验方法假设面板数据中各截面序列具有相同的单位根过程（common unit root process），即假设参数ρi=ρ；另一类为不同根情形下的单位根检验，这类检验方法允许面板数据的各截面序列具有不同的单位根过程（individual unit root process），即允许ρi跨截面变化。

（1）相同根情形下的单位根检验。

①LLC检验。

LLC（Levin-Lin-Chu）检验仍采用ADF检验式形式，即检验时考虑下面的模型：

式中：α=ρ-1，pi为第i个截面成员的滞后阶数，在该模型中允许其跨截面变化。LLC检验的原假设为面板数据中各截面序列均具有一个相同的单位根，备择假设为各截面序列均没有单位根，即H0：α=0，H1：α＜0。虽然LLC检验仍采用ADF检验式形式，但其并没有直接使用Δyit和yi，t-1对参数α进行估计，而是使用Δyit和yi，t-1的代理（proxy）变量去估计参数α。

该检验方法的具体步骤：

首先，在给定各截面成员的滞后阶数pi后，从Δyit和yi，t-1中剔出yi，Δt-j和外生变量的影响，并进行标准化求出代理变量。如果设

式中：和分别为Δyit和yi，t-1对滞后差分项Δyi，t-j以及外生变量回归得到的相应参数的估计值。则Δyit和yi，t-1的代理变量和分别为：

式中：si为模型（16-27）对应于第i个截面成员的ADF检验式的估计标准差。

然后，利用获得的代理变量估计参数α，即用代理变量做回归，估计参数α。此时得到的与参数相对应的t统计量渐近服从标准正态分布。

②Breitung检验。

Breitung检验法与LLC检验法基本类似，原假设为面板审计中的各截面序列均具有一个单位根，并且也是使用Δyit和yi，t-1的代理变量去估计参数α，但Breitung检验法与LLC检验法中代理变量的形式不相同。

式中：βij和分别为Δyit和yi，t-1对滞后差分项Δyi，t-j以及外生变量回归得到的相应参数的估计值。si为模型（A）对应于第i个截面成员的ADF检验式的估计标准差。

则Δyit和yi，t-1的代理变量分别为：(www.xing528.com)

式中：

可见，Breitung检验是先从Δyit和yi，t-1中剔出动态项的影响，然后标准化，之后再退势获得相应的代理变量，最后用代理变量做回归，估计参数α，进而对单位根进行检验。

③Hadri检验。

Hadri检验与KPSS检验类似。原假设为面板数据中各截面序列都不含单位根。计算步骤是首先对面板数据的各截面序列建立如下回归：

然后利用各截面回归的残差项建立LM统计量，统计量的形式有如下两种：

式中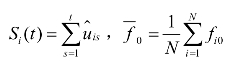：，fi0为第i个截面回归所对应的频率为零时的残差谱密度。

最后根据得到的LM统计量计算Z统计量

式中：参数γ和ω的取值与式（16-34）的回归形式有关，但回归中仅含有常数项时，取值为γ=1/6和ω=1/45，否则γ=1/15，ω=11/6300。在原假设下，Z统计量渐近服从标准正态分布。

（2）不同根情形下的单位根检验。

本书介绍的Im-Pesaran-Skin检验、Fisher-ADF检验和Fisher-PP检验对面板数据的不同截面分别进行单位根检验，其最终的检验在综合了各个截面的检验结果上，构造出统计量，对整个面板数据是否含有单位根做出判断。这几种检验的构造过程如下：

①Im-Pesaran-Skin检验。

在Im-Pesaran-Skin检验中，首先对每个截面成员进行单位根检验：

检验的原假设为：

检验的备择假设：

在对每个截面成员进行单位根检验之后，得到每个截面成员αi的t统计量，记为tiTi（pi），利用每个截面成员αi的t统计量构造检验整个面板数据是否存在单位根的参数α的t统计量如下：

在每个截面成员的滞后阶数为0的情形下，即式子（16-39）中不存在差分项的滞后项，Im-Pesaran-Skin通过模拟给出了统计量在不同显著性水平下的临界值。

如果截面成员中包含滞后项，即（17.2.16）中存在差分项的滞后项，那么Im-Pesaran-Skin检验利用给出了服从一个渐近正态分布的统计量：

因此，可以利用整个渐近正态分布的统计量检验存在滞后项的面板数据。另外，在Im-Pesaran-Skin检验中，还需要设定每个截面成员是否存在截距项或者时间趋势项。

②Fisher-ADF检验和Fisher-PP检验。

Fisher-ADF检验和Fisher-PP检验应用了Fisher的结果（1932），通过结合不同截面成员单位根检验的p值，构造出了两个统计量，渐近服从于卡方分布和正态分布，用来检验面板数据是否存在单位根。

渐近卡方统计量定义如下：

式中：πi为第i组截面成员单位根检验的p值，卡方分布的自由度为2N。

另外，渐近正态分布的定义如下：

式中：Φ-1是标准正态分布函数的反函数，πi为第i组截面数据单位根检验的p值。

Fisher-ADF检验和Fisher-PP检验的原假设和备择假设同Im-Pesaran-Skin检验相同。在进行Fisher-ADF检验时，需要指出每组横截面成员是否包含常数项或者时间趋势项；在进行Fisher-PP检验时，需要指出具体的核函数f0。

5．面板数据的协整检验

经济变量之间存在的长期均衡（静态）关系被称为协整关系，协整分析计算是20世纪80年代以来计量经济学方法论的重大突破，协整关系反映了所研究变量之间存在的一种长期稳定的均衡关系。从经济意义上看，这种协整关系的存在表现为系统内某一变量的变化会影响其它变量的变化，一次冲击只能使协整系统短时间内偏离均衡位置，在长期中它会自动恢复到均衡位置。本章主要介绍三种基于面板数据的协整方法，由于分析的对象是二维数据，所以与时间序列的协整分析并不完全相同。

本书主要介绍Pedroni检验、Kao检验和Fisher检验。Pedroni和Kao协整检验是从Engle-Granger两步（残差）协整检验（1987）发展而来的；而Fisher检验则是合并了的Johansen检验。

6．Pedroni协整检验

Engle-Granger（1987）协整检验是检验I（1）变量进行伪回归的残差发展来的。假如变量之间是协整关系，则残差应该是I（0）变量。相反，假如变量之间不存在协整关系，残差应是I（1）变量。Pedroni（1999，2004）和Kao（1999）扩展了Engle-Granger研究框架，进而研究面板数据。

Pedroni提出了几种协整关系的检验方法，那些方法允许截面间存在异质性截取和趋势系数。可以将模型写为：

式中：t=1，…，T；i=1，…，N；m=1，…，M；假定y和x都是y ，x ～I（1）。参数αi和δi是个体和趋势效应，如果需要可以设为零。

原假设为不存在协整关系，残差eit～I（1）。一般的方法是：先对方程（16-43）进行估计得到残差，然后对残差进行辅助性回归，表达式为

或

每个截面都这样。Pedroni提出了多种检验原假设没有协整关系（ρi=1）的检验统计量。这里有两种假设：同质性假设，即对于所有截面i相同协整关系（ρi=ρ）＜1（Pedroni在截面内检验）；异质性假设，即对于所有i有不同的协整关系ρi＜1（Pedroni在组内检验，截面之间）。

Pedroni协整统计量אN，T是通过对方程（16-45）的残差建立的。根据N和T的大小产生了不同的统计量。Pedroni指出标准的统计量是渐近服从正态分布的：

式中：μ和v是蒙特卡罗实验调整项。

7．Kao协整检验

Kao协整检验基本和Pedroni类似，都是从Engle-Granger检验发展来的，但在第一阶段回归中假定截面间有具体的截取和同质性系数。在Kao（1999）的双变量案例中，我们将模型写为：

式中：yit=yi，t-1+uit，xit=xi，t-1+εit，t=1，…T；i=1，…，N。

一般地，我们也可以考虑模型进行第一阶段回归，截面αi间是不相同的，βi是相同的，所有的趋势系数δi为零。同样，Kao对残差项进行混合辅助回归：

或者混合设定扩展形式：

在没有协整关系的原假设下，Kao给出了检验统计量：

因为p＞0，扩展为

近似收敛于正态分布N（0，1），这里估计方差为，估计的长期运行方差为

协方差为

协方差的估计为：

长期运行协方差由以下式子估计：

式中：k是任意核函数。

8．合并个体检验（Fisher/Johansen）

Fisher（1932）用个体解释变量的检验结果得到合并的协整检验。Maddala和Wu（1999）用Fisher的结果推导出另一种检验面板数据协整关系的方法，该方法从合并个体截面的检验中得到对整个面板的检验统计量。

假设πi为截面成员i个体协整检验的p值，在面板的原假设下，渐近卡方统计量定义如下：

默认地，卡方分布是基于MacKinnon-Haug-Michelis（1999）的p值，并且构造了Johansen的协整检验的两个统计量，迹统计量和极大特征值统计量。