软件操作：使用Correlogram功能进行单位根检验

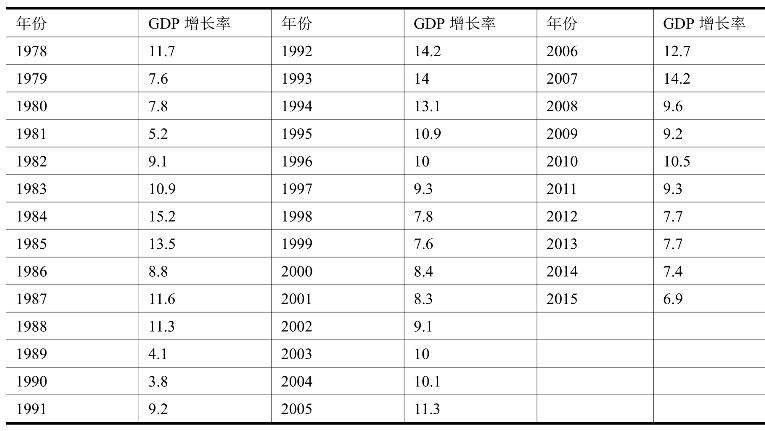
下面以1974—2013年中国人口时间序列数据（见表15-1）为例。

表15-1　中国人口时间序列数据　单位：亿人

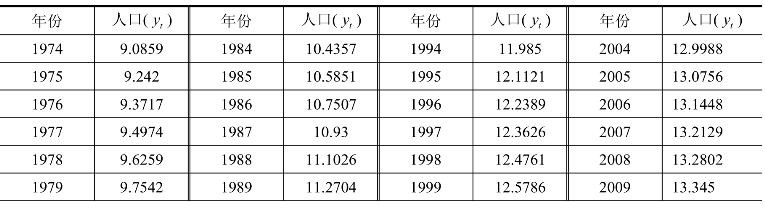
续表

资料来源：《中国统计年鉴》，中国统计出版社，2014。

（1）画时间序列图。

打开工作文件窗口，双击所要选择的中国人口变量yt，从而打开yt的数据窗口。点击View键，选择Graph/Line&Symbol，就可以得到中国人口序列图（见图15-4）。

注：在eviews里面的操作：假设你要产生一阶差分的序列为x，且已经把序列x的数据导入eviews，在命令区键入：“series dx=d（x）”，再按回车键，eviews自然就帮你生成一个新的“dx”序列，即为一阶差分序列；二阶差分同样操作，“series d2x=d（dx）”。

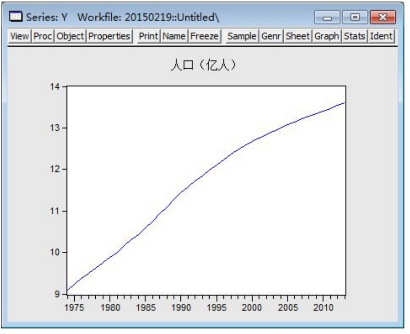
图15-4　中国人口序列图

（2）求中国人口序列的相关图和偏相关图，识别模型形式。

在中国人口序列yt数据窗口中点击View键、选择Correlogram功能，可以得到对话框（见图15-5）。其中包括两种选择：①对原变量（Level）还是对其一阶差分变量（1st difference）、二次差分变量（2st difference）求相关图。此项的默认选择是Level。对于本例，选择Level，即选择对yt画相关图、偏相关图。②另一项选择是确定相关图的滞后期（Lags to include），这里选择的是10。

点击“OK”键，可得到yt的相关图和偏相关图（见图15-6），右侧给出相对于每一个滞后期的估计的自相关系数和偏自相关系数值。Q-Stat所对应的列是相应自由度的Q统计量的值。最右侧Prob列中的数字表示相应自由度条件下χ2统计量取值大于相应Q值的概率。

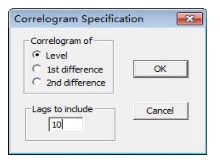
图15-5　选择Correlogram功能得到的对话框

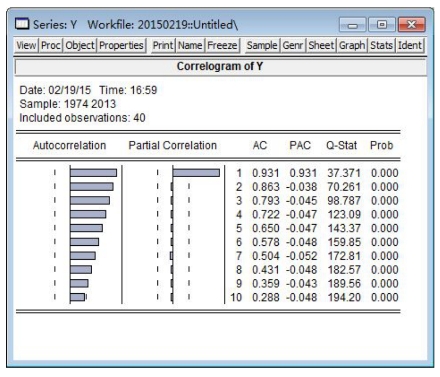
图15-6　yt的相关图和偏相关图

1.单位根检验

表15-2　单位根检验数据

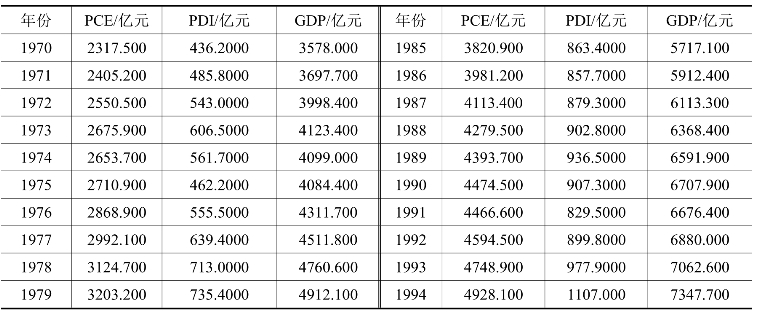
续表

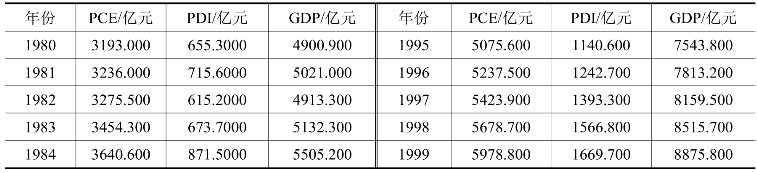
在序列的菜单中选取“View\Unit root test”，打开检验设定窗口（如图15-7）。选择ADF检验，选择水平序列或差分序列进行检验，选择检验式（是否包含漂移和时间趋势），选取最大滞后阶数（Eviews会根据SIC信息准则选择适当的滞后阶），得到检验结果（如图15-8），根据检验结果判定序列的平稳性。

以变量GDP为例，首先检验水平序列（图15-7）的平稳性：检验结果（图15-9）显示GDP非平稳。

其次检验一阶差分序列（图15-8）的平稳性：检验结果（图15-10）显示GDP的一阶差分是非平稳的。即GDP是I（1）过程。

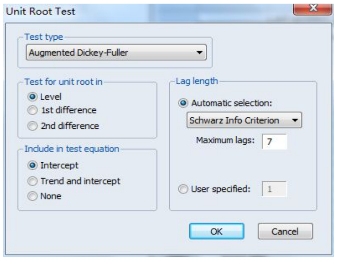
图15-7　检验水平序列的平稳性

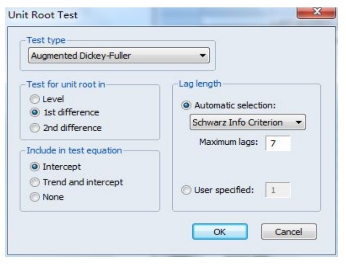
图15-8　检验一阶差分序列的平稳性

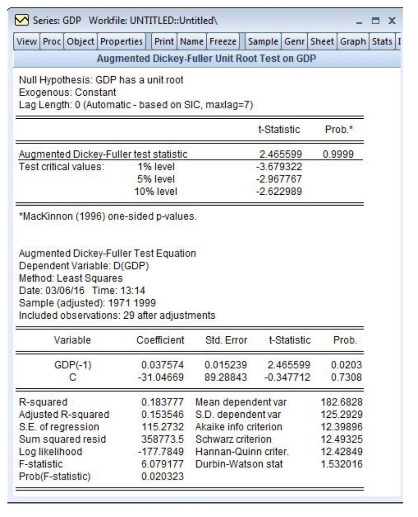
图15-9　检验结果显示GDP非平稳

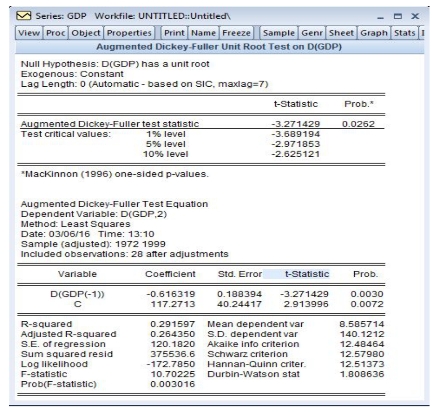
图15-10　检验结果显示GDP的一阶差分是非平稳的

2.EG两步法协整检验

（1）建立回归方程。点击菜单栏里的Quick，选择Estimate Equation。在出现的对话框中依次输入：gdp，c，pdi，如下图15-11所示。

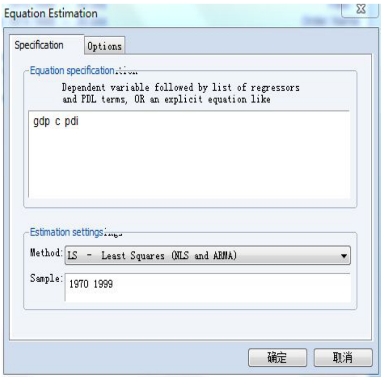
图15-11　建立回归方程对话框

（2）点击确定得到方程回归结果，如图15-12所示。

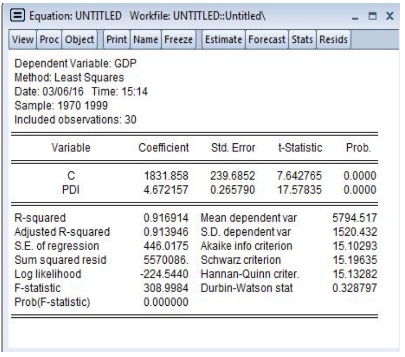
图15-12　方程回归结果对话框

（3）在方程对话框中，单击Proc，选择Make Residual Series，生成方程的残差系列，命名为“e”并对e系列进行ADF单位根检验，检验结果如图15-13所示。(www.xing528.com)

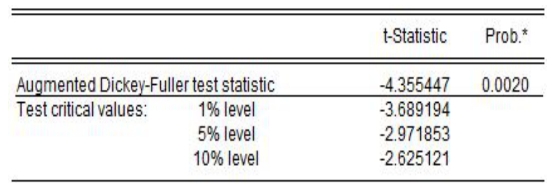
图15-13　ADF单位根检验结果

检验形式为即不包括常数项也不包括趋势项。检验结果表明，在5%的显著性水平下，残差系列是平稳系列，所以GDP和PDI存在协整关系。

3.误差纠正模型

点击菜单栏里的Quick，选择下拉菜单的Estimate Equation，在出现的对话框中一次输入：d（gdp）、c、e（-1）、d（pdi）。其中，e（-1）是误差修正项，d（GDP），d（PDI）表示取GDP和PDI的一阶差分。如图15-14所示。

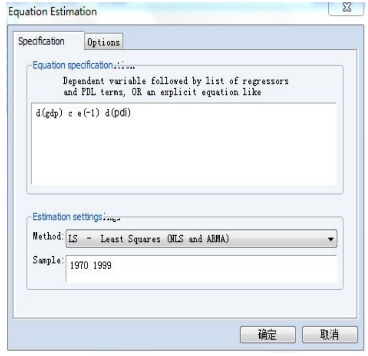
图15-14　GDP和PDI的一阶差分

点击确定，得到误差修正模型的估计结果（见图15-15）。

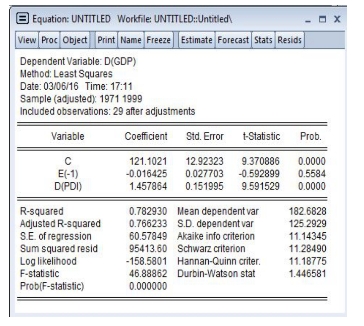
图15-15　误差修正模型的估计结果

4.ARMA模型的识别和估计

表15-3　ARMA模型的识别和估计

注意：ARMA模型的估计要求序列是平稳的，否则要首先进行差分处理，再对差分平稳序列进行识别和估计。本序列已经经过平稳性检验是平稳的。

ARMA模型的估计：以ARMA（1，1）为例。

在模型估计窗口“Quick\Estimate Equation”中设定模型的模式（图15-16），得到估计结果（图15-17）。

图15-16　设定模型的模式

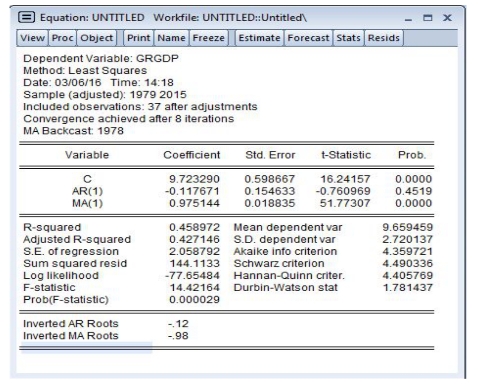
图15-17　模型估计结果

【案例】

从消费水平序列图（见图15-18）可以看出我国居民消费水平基本上保持指数增长趋势。从消费水平序列的变化特征看，这是一个非平稳序列（见图15-19）。

中国居民消费支出模型

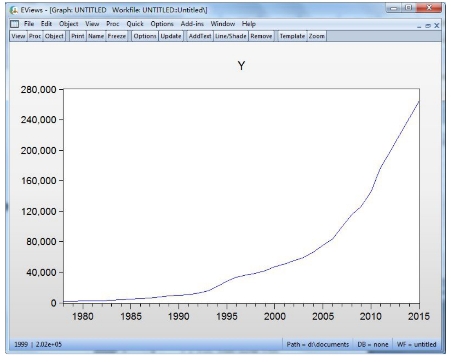
图15-18　居民消费水平序列（1978－2015年）

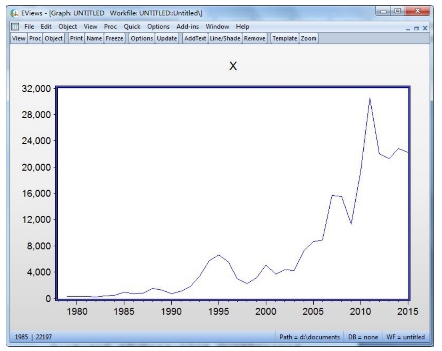
图15-19　消费水平一阶差分序列（1978－2015年）

下面通过对消费水平序列和消费水平差分序列的相关图、偏相关图分析判别其平稳性以及识别模型形式（见图15-20、15-21）。

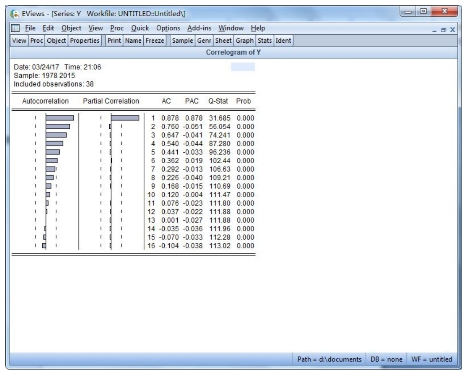
图15-20　yt的相关图，偏相关图

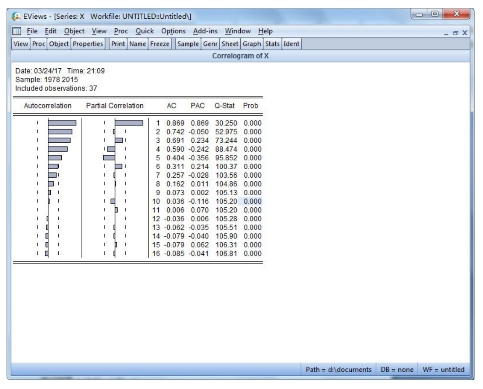
图15-21　一阶差分的相关图，偏相关图

如图15-20和图15-21。消费水平序列yt是非平稳序列，消费水平差分序列Dyt是平稳序列。应该用Dyt建立模型。

下面进行单位根检验，在序列的菜单中选取“View\Unit root test”，打开检验设定窗口。选择ADF检验，选择水平序列或差分序列进行检验，选择检验式（是否包含漂移和时间趋势），选取最大滞后阶数（Eviews会根据SIC信息准则选择适当的滞后阶），得到检验结果（如图15-22），根据检验结果判定序列的平稳性。

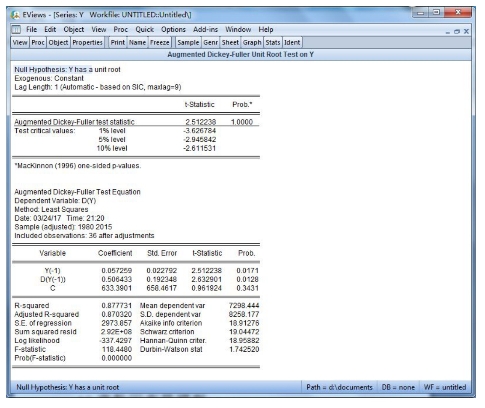
图15-22　单位根检验图

首先检验水平序列的平稳性：检验结果显示yt非平稳。其次检验一阶差分序列的平稳性：检验结果（见图15-22）显示yt的一阶差分是非平稳的，即Dyt是I（1）过程。中国居民消费支出数据如表15-4所列。

表15-4　1978—2015我国居民消费水平数据

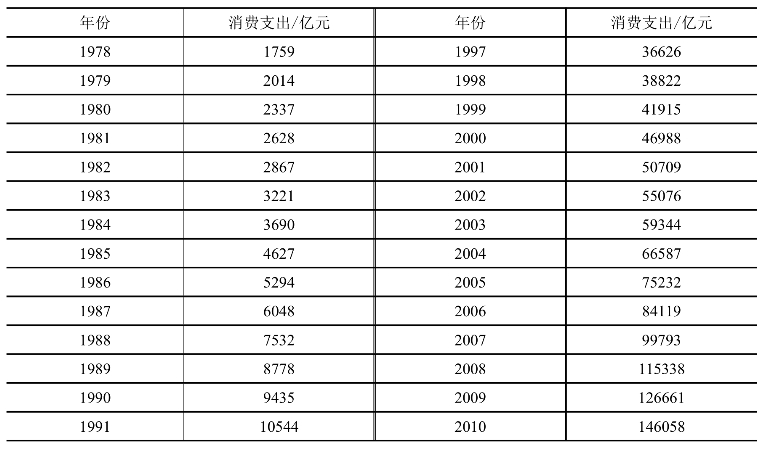
续表

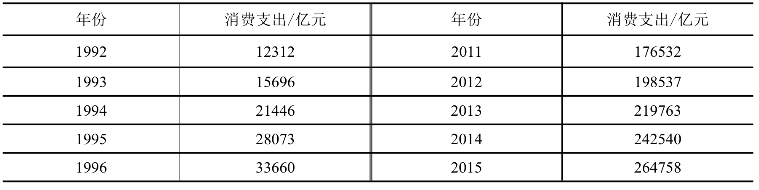
数据来源：中国统计年鉴。