软件操作步骤及实例分析：选择估计方式、结果分析及命名模型

1．联立方程的建立

利用EViews可以建立联立方程组，并对其进行模拟和求解。下面通过一个案例对相关操作过程进行介绍，创造出一个联立方程系统，并使用三阶段最小二乘法进行估计。表14-1给出了我国在1980—2015年的国内生产总值（GDP），居民消费（C）以及固定资产投资（I）和进口（M）情况。

表14-1　1980—2015年中国相关统计数据

续表

数据来源：中国统计年鉴2016。

具体操作步骤如下：

第一步，建立一个Dated-regular frequency（日期-固定频率）工作文件，建立四个序列对象y，cj，i和m，将相关数据导入相应的序列对象中。

第二步，在主菜单中选择Object/New Object/Sytem选项，将弹出一个系统对象空白窗口。在该窗口中对系统方程进行设定，输入如下内容，如图14-1所示。

@inst y(-1)i(-1)m(-1)m(-2)

cj=c(1)+c(2)*y+[ar(1)=c(3)]

i=c(4)+c(5)*y+c(6)*y(-1)+[ar(1)=c(7)]

m=c(8)+c(9)*y+[ar(1)=c(10)]

图14-1　系统方程设定的窗口

输入完毕后单击系统工具对象的Name功能键为所建立的系统命名。其中，系统默认下的名称为sys01、sys02等。

第三步，方程设定好后，单击系统对象工具栏中的Estimate功能键，弹出如图14-2所示的对话框，在Estimation Method选项中选择Three-Stage Least Squares（三阶段最小二乘估计方法），然后点击确定键即可得到估计结果，如图14-3所示。

图14-2　系统估计方法选择估计方式

图14-3　三阶段最小二乘估计方法的结果

第四步，估计结果分析。在图14-3所示的结果中，最上方给出了因变量、估计方法和样本的基本信息。接下来给出了系统估计的所有系数的估计值（Coefficient）、标准差（Std.Error）、t统计量及其伴随概率。在Determinant residual covariance中给出残差值的协方差矩阵的行列式值，本例为4.26×1015。

根据图14-3的结果，可以将方程写为

从结果中可以看出，系统中三个系统的拟合值都在0.98以上，可见拟合度很高，模型的拟合效果很好。

2.联立方程的模拟

操作步骤如下：

第一步，选择主菜单栏中的Object/New Object/Model选项，创建一个空白模型。单击模型对象工具栏中的Name功能键，将其命名为“Model01”。

第二步，在模型对象“Model01”窗口单击鼠标右键，在弹出的菜单中选择“Insert”选项，在弹出窗口的文本框中输入系统对象名称“：sys01”，即可将系统对象sys01导入模型中。

第三步，将模型中的系统转换为内置文本形式。选择模型对象“Model01”窗口工具栏中的Proc/Links/Break All Links-Make all quations inlines选项，即可得到图14-4所示的窗口。每一个文本中列出一个方程对象，右侧为方程的函数形式。双击TEXT后面的方程即可查看完整的方程形式。

图14-4　显示模型对象中方程的文本形式

3.联立方程模型的求解(www.xing528.com)

具体操作步骤如下：

第一步，打开模型对象“Model01”。

第二步，在模型对象工具栏中选择Solve功能键，在弹出的对话框的Basic Options选项卡中进行设定。在Simulation type中选择Deterministic，在Dynamics中选择Dynamics solution，并选择Structural（ignore ARM）复选框。在Solution sample中输入样本区间1980 2015。对于剩余的各选项卡内容按系统默认值进行设定，如图14-5所示。

图14-5　模型对象求解设定的对话框

第三步，然后单击确定即可得到模型的解，如图14-6所示。其中显示了操作区间、样本区间、求解方法等基本信息。Dynamics-Deterministic Simulation为确定模拟，预测时使用求解样本期之前的内生变量；最大迭代次数为5000；情景分析为实际“baseline”情景分析。

图14-6　模型对象的解

【案例】

中国私人轿车拥有量决定因素分析

1985—2015年中国私人轿车拥有量以年增长率15.93%，年均增长453万辆的速度飞速增长（见图14-7）。

图14-7　1985—2015年私人轿车数量散点图

考虑到目前农村家庭购买私人轿车的现象还很少，在建立中国私人轿车拥有量模型时，主要考虑如下因素：（1）城镇居民家庭人均可支配收入；（2）城镇总人口；（3）轿车产量；（4）公路交通完善程度；（5）轿车价格。

“城镇居民家庭人均可支配收入”、“城镇总人口数”和“轿车产量”可以直接从统计年鉴上获得。“公路交通完善程度”用全国公路里程度量，也可以从统计年鉴上获得。由于国产轿车价格与进口轿车价格差距较大，而且轿车种类很多，做分种类的轿车销售价格与销售量统计非常困难，所以因素“轿车价格”暂且略去不用。定义变量名如下：

Y：中国私人轿车拥有量（万辆）

X1：城镇居民家庭人均可支配收入（元），

X2：全国城镇人口（亿人）

X3：全国汽车产量（万辆）

X4；全国公路长度（万km）

图14-8　相关系数图

图14-9　回归结果图

看相关系数阵，Y与X1，X2，X3，X4的相关系数都在0.9以上，但输出结果中，解释变量X3、X4的回归系数却通不过显著性检验，这预示着解释变量之间可能存在多重共线性。

看散点图，把Y与X1，X2处理成线性关系，把Y与X3处理成幂函数（抛物线）关系，并删除变量X4得结果如图14-10所示。

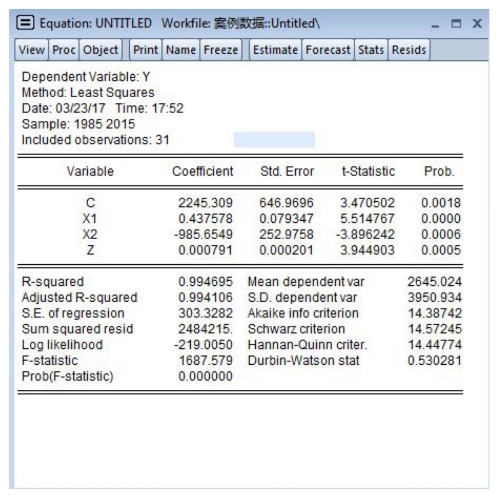
图14-10　回归结果图

每个变量都具有很高的显著性。拟合优度也提高了，没有异方差。

表14-2　相关数据表

续表

数据来源：《中国统计年鉴》，汽车工业年鉴，中国统计出版社，1986—2016。