软件操作的优化策略及OLS法估计模型分析

以GDP的影响因素为例，介绍多重共线性在EViews中的应用，模型如下：

式中：FDI代表外商直接投资，NX代表净出口，G代表政府支出，详细数据如表13-1所示。

表13-1　1985—2015年我国实际外商投资、国内生产总值、净出口和政府支出情况

续表

数据来源：《中国统计年鉴2016》。

具体操作步骤如下：

第一步，创建相应的工作文件，输入相关的变量数据

第二步，生成一个包含FDI、NX、G三个序列对象的群对象，命名为“group01”，通常默认建立的第一个群对象的名称即为“group01”。

第三步，在群对象“group01”的工具栏中，选择Quick/Group Statistics/Correlation选项，即可弹出如图13-1所示的变量间的相关系数。如图所示，政府购买G与净出口NX之间的相关系数达到0.87以上，因而两个变量之间可能存在线性关系，即模型有多重共线性的可能。

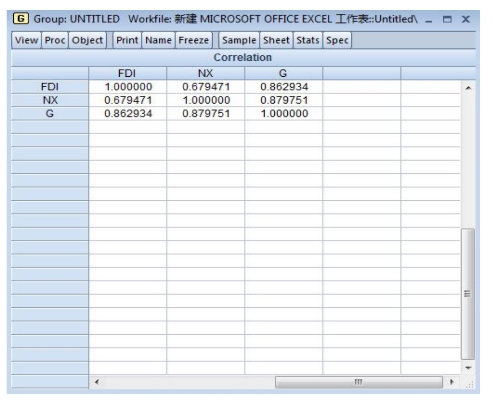
图13-1　解释变量间的相关系数

【案例】

本案例选取1991—2015年中的电信业务数量（百亿笔）作为被解释变量，1991—2015年的邮政业务数量（百亿笔）、中国人口数（亿人）、市镇人口占比和人均GDP（万元）变量作为解释变量。具体数据如表13-2所示。

表13-2　相关数据表

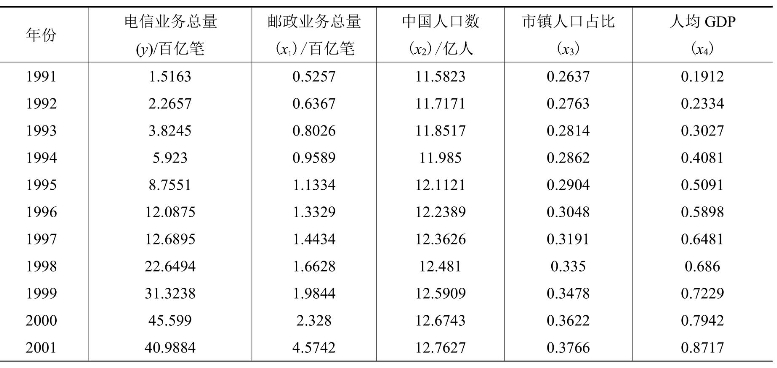
续表

数据来源：《中国统计年鉴2016》。(www.xing528.com)

（1）多重共线性检验。

首先，绘制相关图，确定模型的函数形式。

通过对原始数据的散点图（见图13-2）观察可以看出：被解释变量——电信业务数量呈指数化增加，而解释变量并无此特征变化，故将被解释变量进行取对数处理，以便于模型设定。解释变量分别为：邮政业务总量（x1）、中国人口数（x2）、市镇人口占比（x3）、人均GDP（x4）。

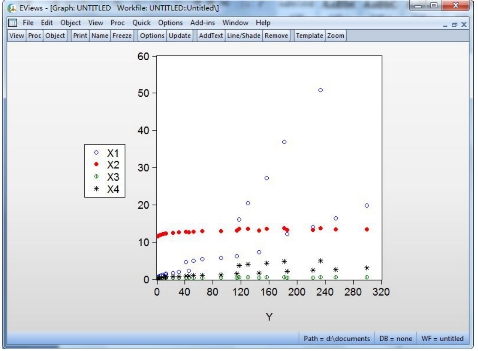
图13-2　原始数据散点图

其次，利用OLS法估计模型，估计结果如图13-3所示。

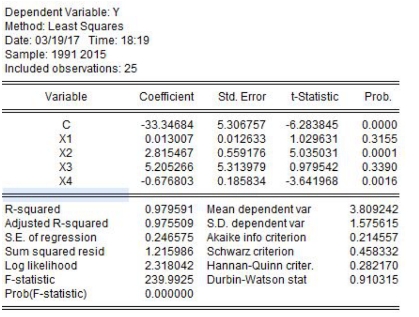
图13-3　回归结果图

通过检验结果发现：x1、x3系数的显著性水平未通过5%的检验，而x2、x4的显著性水平较高。同时，该模型的可决系数R2为0.98，模型对于被解释变量的解释程度较高。但是由于解释变量中x1和x3未通过显著性检验，同时经过分析可以看出模型解释变量之间很可能存在多重共线性。

利用EViews进行相关系数检验，得到如图13-4所示相关系数矩阵。

图13-4　相关系数图

由表13-4可知，每个解释变量都与电信业务数量高度相关，解释变量之间也是高度相关的，说明存在多重共线性。按照逐步回归法先建立一元回归模型。根据理论分析，中国人口数应该是电信业务数量最主要的影响因素；相关系数检验也表明，中国人口数与电信业务数量的相关性最强。所以把Yi=β0+β1x2i+ei作为最基本的模型。将其余变量逐个引入模型，估计结果如表13-3所示（括号里的数字为t统计量）。

表13-3　电信业务数量函数逐步回归分析结果

从表13-3中的估计结果可以看出，在基本模型引入第二个变量之后，拟合优度均有所提高，并且模型y=f（x2，x4）的拟合优度最高，故选定x2、x4作为其中的两个解释变量，继续添加变量，但是从表中的回归结果可以看出，效果不好，故选定双解释变量的多元线性回归模型，且解释变量为x2、x4。

经过以上的逐步引入检验过程，最终确定的函数为：

y=－37.60203+3.290111x2－0.444151x4

(－18.839 04)(20.072 06)(－6.422 120)

R2=0.977732，R2=0.975708，F=482.9824，DW=0.989487

从各系数的t统计量可以看出，均不显著为零，且模型的拟合优度较高，对被解释变量的解释程度较高，同时模型有效的消除了多重共线性。