误差项一阶自相关与DW值的关系及意义研究

1.非自相关假定

回归模型的假定条件之一是，

即误差项ut的取值在时间上是相互无关的。称误差项ut非自相关。如果

则称误差项ut存在自相关。

自相关又称序列相关，原指一随机变量在时间上与其滞后项之间的相关，在这里是指回归模型中的残差项之间存在相关关系。但是值得注意的是，自相关也是相关关系的一种。

2．一阶自相关

自相关按形式可分为两类。

（1）一阶自回归形式。

当误差项ut只与其滞后一期值有关时，即

则称ut具有一阶自回归形式。

（2）高阶自回归形式。

当误差项ut的本期值不仅与其前一期值有关，而且与其前若干期的值都有关系时，即

则称ut具有高阶自回归形式。

在当前计量经济学的研究中，最常见形式是一阶自回归，所以我们重点讨论误差项的线性一阶自回归形式，即

式中：α1是自回归系数，yt是随机误差项。yt满足通常假设

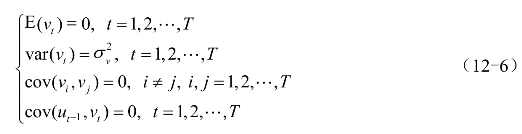
依据普通最小二乘法公式，模型中α1的估计公式是，

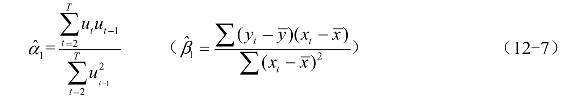
式中：T是样本容量。若把ut，ut-1看作两个变量，则它们的相关系数是

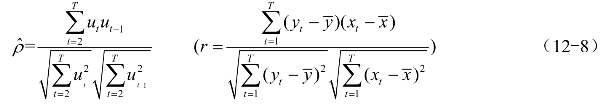
对于大样本显然有

代入上式，可得

因而对于总体参数有ρ =α1，即一阶自回归形式时，其自回归系数等于残差项与其滞后一期残差项的相关系数。因此原回归模型中误差项ut的一阶自回归形式可表示为，

ρ的取值范围是[-1，1]。当ρ＞0时，称ut存在正自相关；当ρ＜0时，称ut存在负自相关。当ρ=0时，称ut不存在自相关。为了方便读者理解时间序列的正、负自相关特征，下面分别给出变量对其一阶滞后变量的散点图，图12-1、12-2、12-3所示分别为具有非自相关、正自相关和负自相关的三个序列。如图所示，当扰动项的估计值呈循环型，并不频繁地改变符号，而是相继若干个正值以后跟着几个负值，则表明存在正自相关；而如果扰动项的估计值呈锯齿形，即扰动项随时间逐次修改符号，表明存在负自相关。

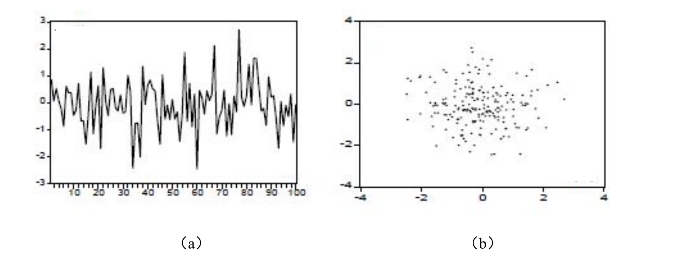
图12-1　非自相关序列图

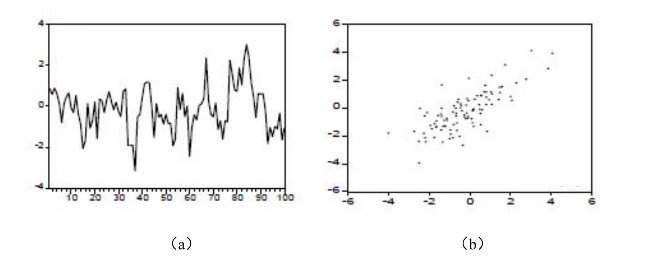
图12-2　正自相关序列图

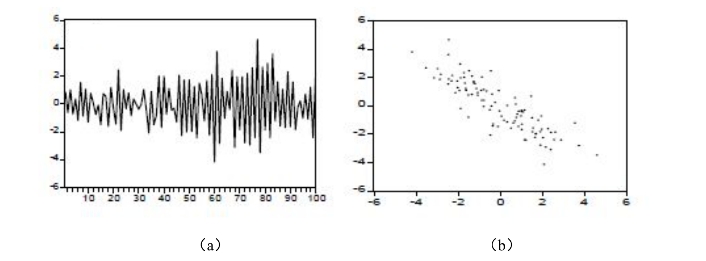
图12-3　负自相关序列图

下面推导当误差项ut为一阶自回归形式时，ut的期望、方差与协方差公式。由上式有

因为对于平稳序列有，整理上式得

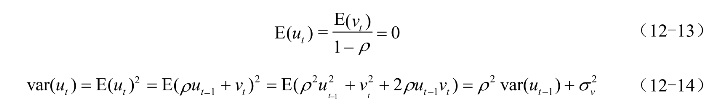
整理可得

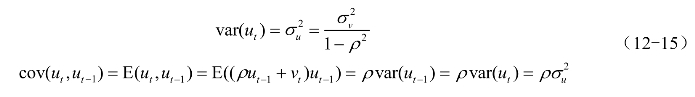
同理

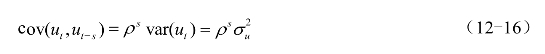
令，则整理上述公式可得

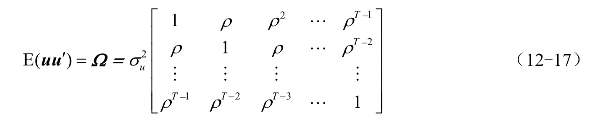
从而验证了当回归模型的误差项ut存在一阶自回归形式时，。同理也可证明当ut存在高阶自回归形式时，仍有。

3.自相关的来源与后果

误差项存在自相关，主要有如下几个原因。

（1）模型的数学形式不妥。若所用的数学模型与变量间的真实关系不一致，误差项常表现出自相关。比如平均成本与产量呈抛物线关系，当用线性回归模型拟合时，由于平方项未被包含进入方程内，因此其被处理为误差项，故自相关性必定存在。

（2）惯性。大多数经济时间序列都有一个明显的特点，就是它的惯性。众所周知，GDP、价格指数、生产、就业和失业等时间序列都呈现周期循环。相继的观测值很可能是相互依赖的。

（3）蛛网现象。许多农产品的供给表现出一种所谓的蛛网现象。例如，供给对价格的反应要滞后一个时期。今年的作物种植是受去年流行的价格影响的，因此误差项有很大可能时相关的。

当误差项ut存在自相关时，模型参数的最小二乘估计量具有如下特性。

（1）只要假定条件cov（X′u）=0成立，回归系数仍具有无偏性。

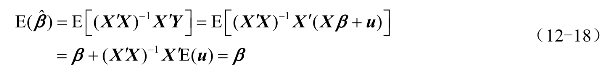
以一元线性回归模型为例：

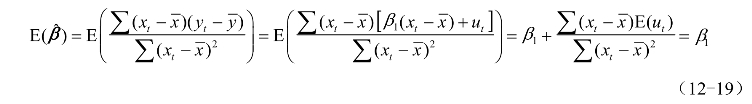
（2）丧失有效性。

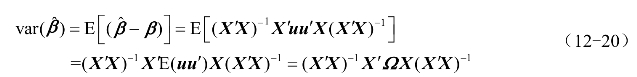
与不等。

以一元线性回归模型，，为例，当ut非自相关时

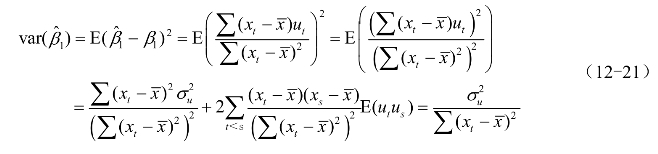
当ut为一阶自回归形式时

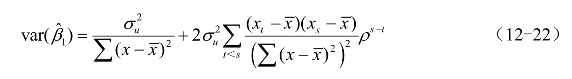(www.xing528.com)

的方差比ut非自相关时大，失去有效性。低估回归参数估计量的方差，等于夸大了回归参数的抽样精度

过高的估计统计量t的值，从而把不重要的解释变量保留在模型里，使显著性检验失去意义。

（3）有可能低估误差项ut的方差。

（4）和都变大，都不具有最小方差性。所以用依据普通最小二乘法得到的回归方程去预测，预测是无效的。

4.自相关检验

下面介绍三种判别与检验方法。

（1）图示法。

图示法就是依据残差对时间t的序列图作出判断。由于残差是对误差项ut的估计，所以尽管误差项ut观测不到，但可以通过的变化判断ut是否存在自相关。

图示法的具体步骤是，①用给定的样本估计回归模型，计算残差ut，（t=1，2，…T），绘制残差图；②分析残差图。若残差图与图12-1类似，则说明ut不存在自相关；若与图12-2类似，则说明ut存在正自相关；若与图12-3类似，则说明ut存在负自相关。

经济变量由于存在惯性，不可能表现出如图12-3那样的震荡式变化。其变化形式常与图12-2相类似，所以经济变量的变化常表现为正自相关。

（2）D-W（Durbin-Watson）检验法。

D-W检验是J.Durbin、G.S.Watson于1950、1951年提出的。它是利用残差构成的统计量推断误差项ut是否存在自相关。使用D-W检验，应首先满足如下三个条件。

（1）误差项ut的自相关为一阶自回归形式。

（2）因变量的滞后值y1-t不能在回归模型中作解释变量。

（3）样本容量应充分大（T＞15）

D-W检验步骤如下。给出假设：

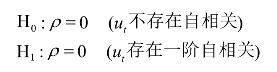
用残差值计算统计量D-W

式中：分子是残差的一阶差分平方和，分母是残差平方和。把上式展开，

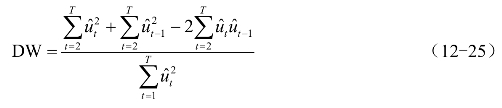
因为当样本充分大时，有

结合上式可得

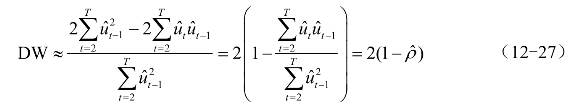
因为ρ的取值范围是[-1，1]，所以DW统计量的取值范围是[0，4]。ρ与DW值的对应关系见表12-1。

表12-1　ρ与DW值的对应关系及意义

续表

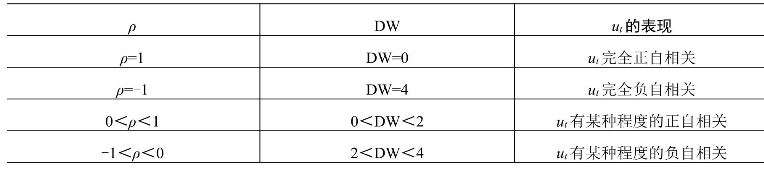
实际中DW=0，2，4的情形是很少见的。当DW取值在（0，2），（2，4）之间时，怎样判别误差项ut是否存在自相关呢？推导统计量DW的精确抽样分布是困难的，因为DW是依据残差计算的，而的值又与ut的形式有关。DW检验与其它统计检验不同，它没有唯一的临界值用来制定判别规则。然而Durbin-Watson根据样本容量和被估参数个数，在给定的显著性水平下，给出了检验用的上、下两个临界值du和d1。判别规则如下：

（1）若DW取值在（0，d1）之间，拒绝原假设H0，认为ut存在一阶正自相关。

（2）若DW取值在（4-d1，4）之间，拒绝原假设H0，认为ut存在一阶负自相关。

（3）若DW取值在（du，4-du）之间，接受原假设H0，认为ut非自相关。

（4）若DW取值在（d1，du）或（4-du，4-d1）之间，这种检验没有结论，即不能判别ut是否存在一阶自相关。判别规则可用图12-4表示。

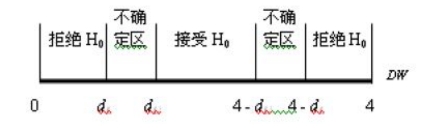
图12-4　判别规则

当DW值落在“不确定”区域时，有两种处理方法。①加大样本容量或重新选取样本，重作DW检验。有时DW值会离开不确定区。②选用其它检验方法。

DW检验表给出DW检验临界值。DW检验临界值与三个参数有关。①检验水平α；②样本容量T；③原回归模型中解释变量个数k（不包括常数项）。

注意：

①因为DW统计量是以解释变量非随机为条件得出的，所以当有滞后的内生变量作解释变量时，DW检验无效。这时的表现是DW值常常接近2。当估计式为

时，Durbin认为应该用下面的h统计量检验一阶自相关。

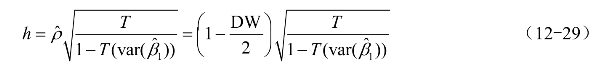
Durbin已证明h统计量近似服从均值为零，方差为1的标准正态分布。可以用标准正态分布临界值对h的显著性作出检验。注意：当时检验无效。

②不适用于联立方程模型中各方程的序列自相关检验。

③DW统计量不适用于对高阶自相关的检验。

5.克服自相关

如果模型的误差项存在自相关，首先应分析产生自相关的原因。如果自相关是由于错误地设定模型的数学形式所致，那么就应当修改模型的数学形式。怎样查明自相关是由于模型数学形式不妥造成的？一种方法是用残差对解释变量的较高次幂进行回归，然后对新的残差作DW检验，如果此时自相关消失，则说明模型的数学形式不妥。

如果自相关是由于模型中省略了重要解释变量造成的，那么解决办法就是找出略去的解释变量，把它做为重要解释变量列入模型。一种方法是用残差对那些可能影响因变量但又未列入模型的解释变量回归，并作显著性检验，从而确定该解释变量的重要性。如果是重要解释变量，应该列入模型。

只有当以上两种引起自相关的原因都消除后，才能认为误差项ut“真正”存在自相关。在这种情况下，解决办法是变换原回归模型，使变换后的随机误差项消除自相关，进而利用普通最小二乘法估计回归参数。这种变换方法称作广义最小二乘法。下面介绍这种方法。

设原回归模型是

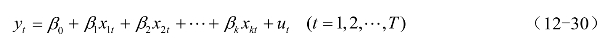
其中ut具有一阶自回归形式

其中vt满足通常的假定条件，把上式代入上式，

进行处理得到

令

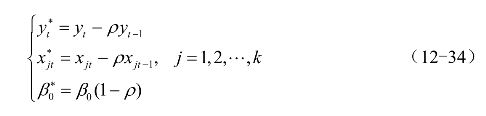
则可得到以下表达式

上述变换称作广义差分变换。上式中的误差项vt是非自相关的，满足假定条件，所以可对上式应用最小二乘法估计回归参数。上式中的β1，…，βk就是原模型中的β1，…，βk，而与模型中的β0有如下关系：