软件操作及线性关系分析、回归模型和异方差分析

已知某地区的个人储蓄Y，可支配收入X的截面样本数据如表11-1所示，建立两者之间的线性计量经济模型并估计。

表11-1　相关数据表

续表

输入命令“scatter x y”，即可得到如图11-8所示窗口。

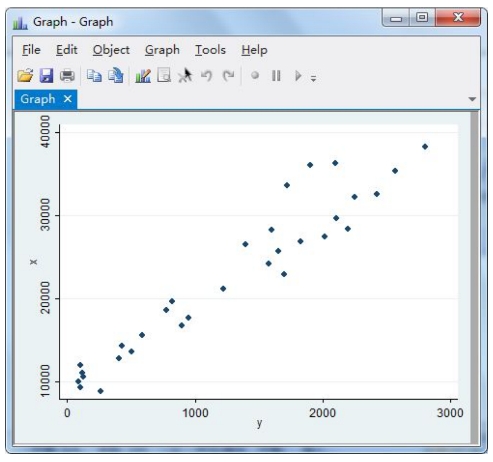
图11-8　散点图

由上图可以看出，两者之间存在明显的线性关系，故设置如下一元回归模型：

操作步骤如下。

第一步，分布滞后模型的建立。在主菜单中选择Quick/Estimate Equation选项，或者在工作文件窗口的工具栏中选择Object/New Object/Equation选项，弹出方程设定的对话框，如图11-9所示。

图11-9　操作图

在上述所示的文本框中列出被解释变量和解释变量，在“Method”中选择“LS”估计法，然后点击确定，即可得到如图11-10所示的估计结果。从图中可以看出，在5%的显著性水平下β1、β2通过了t检验，但是常数项和β3未通过检验。改模型拟合优度达到0.91，因而模型的拟合效果很好。

图11-10　回归结果图

第二步，生成回归模型的残差图。模型完成后，系统会将残差保存到序列对象Resid中。双击工作文件中的Resid序列对象，在打开的窗口中，选择View/Graph/Line选项，得到回归方程的残差图，如图11-11所示。

图11-11　残差图

从上图可以看出，随着拟合值和x的值的增大，扰动项的方差波动在加剧，说明存在异方差。

第三步，残差序列的white检验。在11-11页面，在工具栏中选择View/Residual Diagnostics/white选项，点击确定，如图11-12所示。

图11-12　怀特检验图

原假设H0为该回归模型不存在异方差。其中F-statistic是辅助方程整体显著性的F统计量；Obs*R-squared是White检验的统计量NR2，其概率值是0.0106，明显小于常规的检验水平0.05，因此拒绝怀特检验原假设，认为原方程的残差序列存在异方差，需要对原模型进行相应的修正以解决异方差的影响。(www.xing528.com)

【案例】

农作物产值模型——检验

取2015年中国31个省（市、自治区）农作物种植业产值yt（亿元）和农作物播种面积xt（万亩，1亩≈666.67m2）数据（见表11-2），研究二者之间的关系。得估计的线性模型如下，

表11-2　2015年中国31个省（市、自治区）农作物种植业产值和农作物播种面积数据

无论是从yt和xt观测值的散点图（见图11-13）还是模型的残差图（见图11-14）都可以发现数据中存在异方差。

图11-13　农作物产值yt和播种面积xt

图11-14　残差图

（1）用White方法检验是否存在异方差。

在上式回归的基础上，做White检验（见图11-15）。

图11-15　操作图

得结果如图11-16所示。

图11-16　white检验结果图

注意：输出结果中的概率是指χ2（2）统计量取值大于8.02的概率为0.05，所以存在异方差。

（2）用Goldfeld-Quandt方法检验是否存在异方差。

①首先以xt为基准对成对样本数据（yt，xt）按取值大小排序。

②去掉中间7个数据，按xt取值大小分成样本容量各为12的两个子样本。

③用两个子样本各自回归得结果如下：

因为F=4.818＞F0.05（9，9）=3.18，所以存在异方差。