异方差检验方法的分析介绍

1.定性分析异方差

（1）经济变量规模差别很大时容易出现异方差。如个人收入与支出关系，投入与产出关系。

（2）利用散点图（如图11-6所示）做初步判断。

（3）利用残差图（如图11-7所示）做初步判断。

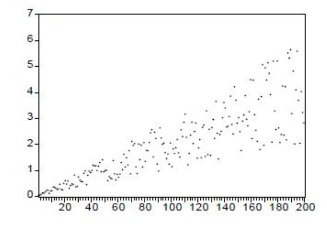
图11-6　散点图

图11-7　残差图

2.定量分析异方差

（1）White检验。

White检验由H.White 1980年提出。Goldfeld-Quandt检验必须先把数据按解释变量的值从小到大排序。Glejser检验通常要试拟合多个回归式。White检验不需要对观测值排序，也不依赖于随机误差项服从正态分布，它是通过一个辅助回归式构造χ2统计量进行异方差检验。White检验的具体步骤如下。以二元回归模型为例：

①先对上式进行OLS回归，求残差。

②做如下辅助回归式，

即用对原回归式中的各解释变量、解释变量的平方项、交叉积项进行OLS回归。注意，上式中要保留常数项。(www.xing528.com)

③White检验的零假设和备择假设是

④在不存在异方差假设条件下，统计量

式中T表示样本容量，R2是辅助回归式的OLS估计式的可决系数。自由度5表示辅助回归式中解释变量项数（注意，不计算常数项）。TR2属于LM统计量。

⑤判别规则

（2）ARCH检验。

异方差的另一种检验方法称作自回归条件异方差（ARCH）检验。这种检验方法不是把原回归模型的随机误差项看作xt的函数，而是把看作误差滞后项，…的函数。ARCH是误差项二阶矩的自回归过程。恩格尔（Engle，1982）针对ARCH过程提出LM检验法。辅助回归式定义为

LM统计量定义为

式中R2是辅助回归式的可决系数。在H0∶α1=…=αn=0成立条件下，ARCH渐近服从χ2（n）分布。ARCH检验的最常用形式是一阶自回归模型（n=1）：

在这种情形下，ARCH渐近服从χ2（1）分布。