软件操作的优化效果：利用EViews进行回归分析

通过本例介绍两种非线性回归模型的估计方法：（1）通过线性化的方式估计非线性回归模型；（2）直接估计非线性回归模型。

某硫酸厂生产的硫酸的透明度指标一直达不到优质要求，经分析透明度低与硫酸中金属杂质的含量太高有关。影响透明度的主要金属杂质是铁、钙、铅、镁等。通过正交试验的方法发现铁是影响硫酸透明度的最主要原因。测量了30组样本值，数据见表9-1，硫酸透明度（y）与铁杂质含量（x）的散点图如图9-10，应该建立非线性回归模型。

表9-1　硫酸透明度（y）与铁杂质含量（x）数据

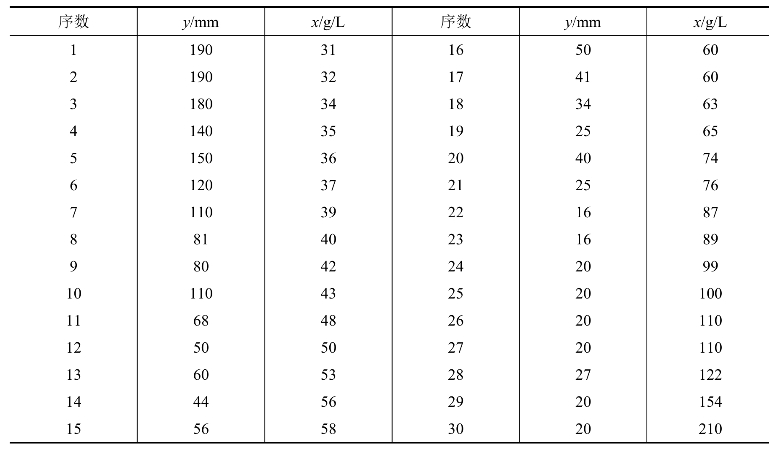
（1）通过线性化的方式估计非线性回归模型。

先建立倒数模型。从工作文件主菜单中点击Quick键，选择Estimate Equation功能，在弹出的对话框的Equation Specification（方程设定）选择框中输入

点击“确定”，得到估计结果如图9-11。对应的表达式是：

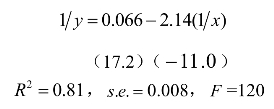
可决系数R2=0.81。

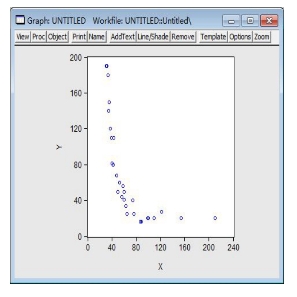
图9-10　硫酸透明度（y）与铁杂质含量（x）的散点图

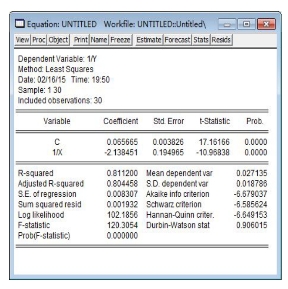
图9-11　倒数模型结果

实际上，如果建立指数函数，拟合的效果会更好。打开方程设定（Equation Specification）对话框，输入估计命令，

log（y）c 1/x

点击“确定”，得到估计结果如图9-12。对应的表达式是：

lny=2.10 +99.2(1x)

(20.2)(18.7)

R2=0.93，s.e.=0.23，F=351

可决系数由0.81提高至0.93，可见拟合为指数函数比倒数函数更好。

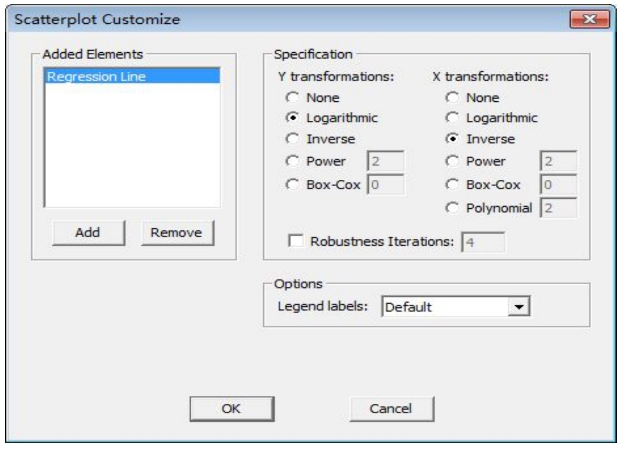
散点图与拟合的指数曲线见图9-13。EViews操作步骤是，打开x、y数据组窗口，点击View键选Graph type/Scatter，在Details/Fit lines中选择Regression Line（见图9-14），再点击Options弹出对话框，在对话框中y选对数形式，x选倒数形式（见图9-15），点击“确定”后，再在如图9-14所示的对话框中点击“确定”，就可以得到如图9-13所示窗口。

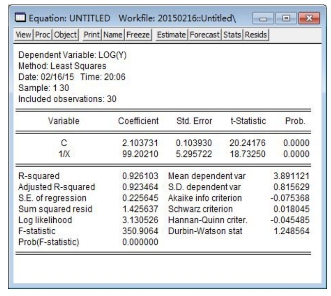
图9-12　指数函数估计结果

注意：对数变量和倒数变量也可以通过点击Quick键，选择Generate Series功能先定义成新变量，然后用新变量名列写出估计命令。比如先把对数变量log（y）定义为lny，倒数变量1/x定义为z。估计命令写为：

回归参数的估计结果是一样的，但不如估计命令“log（y）c 1/x”好。原因是预测时，前者只是得到lny的预测值，而后者既可以得到lny的预测值，也可以得到y的预测值，而通常更关心y的预测结果。

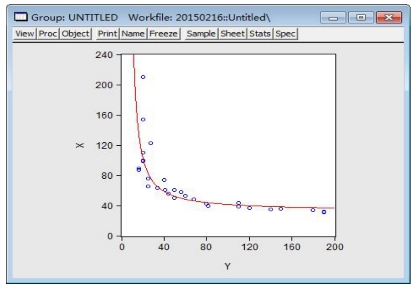
图9-13　散点图与拟合的指数曲线

图9-14　在Details/Fit lines中选择Regression Line

(www.xing528.com)

图9-15　y选对数形式，x选倒数形式

【案例】

中国从20世纪30年代开始生产铅笔。起初，全国有22个厂家生产铅笔。产量居世界首位（33.9亿支），占世界总产量的1/3。改革开放以后，铅笔生产增长极为迅速。1979—1983年平均年增长率为8.5%。铅笔销售量时间序列见图9-16。1961—1964年的销售量平稳状态是受到了经济收缩的影响。1969—1972年的增长是由于一度中断了的中小学教育逐步恢复的结果。1977—1978年的增长是由于高考正式恢复的结果。1981年中国开始生产自动铅笔，对传统铅笔市场冲击很大。1979—1985年的缓慢增长是受到了自动铅笔上市的影响。

初始确定的影响铅笔销量的因素有全国人口、各类在校人数、设计人员数、居民消费水平、社会总产值、自动铅笔产量、价格因素、原材料供给量、政策因素等。经过多次筛选、组合和逐步回归分析，最后确定的被解释变量是yt（铅笔年销售量，千万支），解释变量分别是xt1（自动铅笔年产量，百万支），xt2（全国人口数，百万人），xt3（居民年均消费水平，元），xt4（政策变量）。因政策因素影响铅笔销量出现大幅下降时，政策变量取负值。数据见表9-2。

由图9-17知自中国生产自动铅笔起，自动铅笔产量与铅笔销量存在线性关系。由图9-18知全国人口与铅笔销量存在线性关系。说明人口越多，对铅笔的需求就越大。由图9-19知居民年均消费水平与铅笔销量存在近似对数的关系。散点图说明居民年均消费水平越高，则铅笔销量就越大。但这种增加随着居民消费水平的增加变得越来越缓慢。图9-20显示政策变量与铅笔销量也呈线性关系。

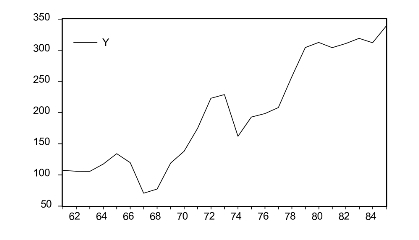
图9-16　铅笔销售量时间序列（1961—1985）

表9-2　1961—1985年的影响铅笔销量的因素

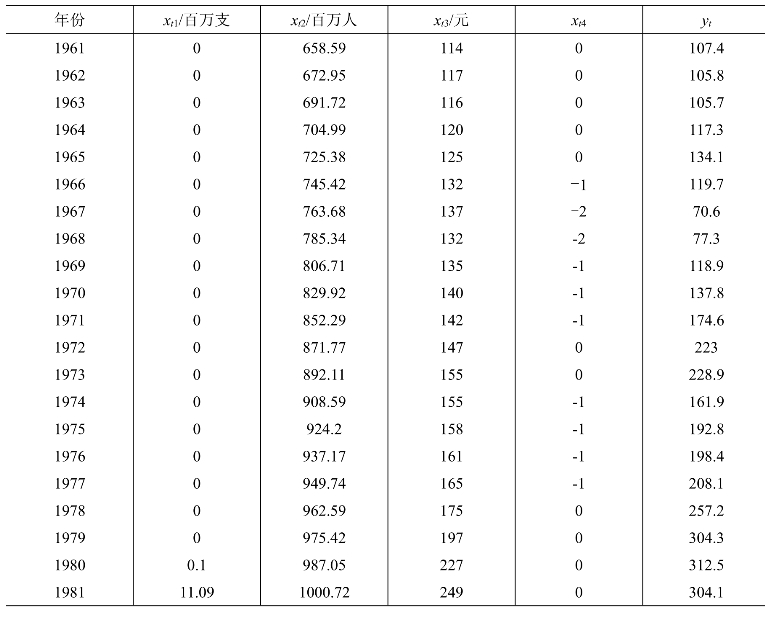
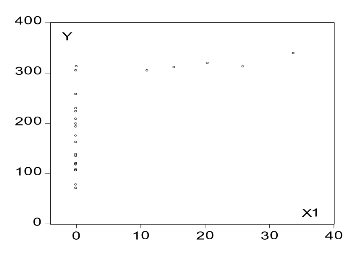
图9-17　yt—xt1散点图

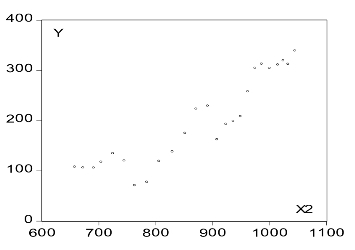
图9-18　yt—xt2散点图

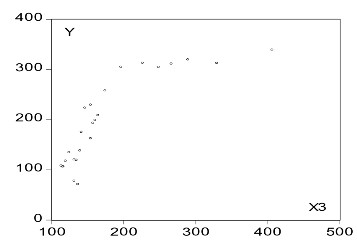
图9-19　yt—xt3散点图

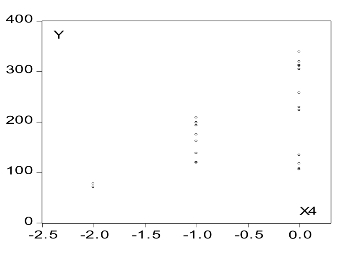
图9-20　yt—xt4散点图

基于上述分析建立的模型形式是

yt与xt3呈非线性关系。利用EViews进行回归，得到如下结果：

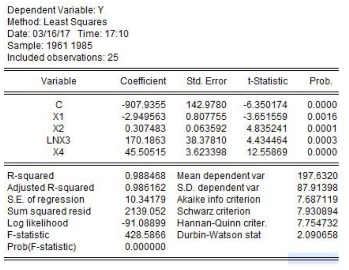
图9-21　回归结果

估计结果如下。

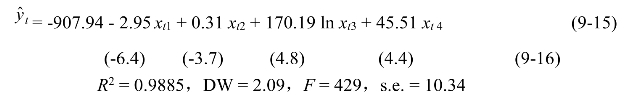
上式说明，在上述期间自动铅笔年产量每增加1百万支，平均使铅笔的年销售量减少2950万支。全国人口数每增加1百万人，平均使铅笔的年销售量增加310万支。对数的居民年均消费水平每增加1个单位，平均使铅笔的年销售量增加17亿支。一般性政策负面变动使铅笔的年销售量减少4.551亿支。当政策出现大的负面变动时，铅笔的年销量会减少9.102亿支。

当yt对所有变量直接进行线性回归时，EViews结果如图9-22所示。

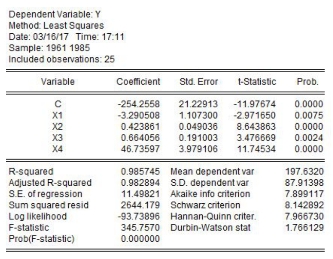
图9-22　直接回归结果

显然估计结果不如（9-14）式好。