理论基础：可线性化的非线性模型及其图形分析

上两章介绍了线性回归模型。但有时候变量之间的关系是非线性的，特别是待估参数与被解释变量之间是非线性的。例如：

上述非线性回归模型，是无法用最小二乘法估计参数的，但是可以使用非线性方法进行估计。另外一种非线性回归模型，虽然其形式是非线性的，但可以通过适当的变换，转化为线性模型，然后利用线性回归模型的估计与检验方法进行处理。称此类模型为可线性化的非线性模型。下面介绍几种典型的可以做线性化处理的非线性模型。

（1）指数函数模型。

b＞0和b＜0两种情形的图形分别见图9.1和9.2。显然xt和yt的关系是非线性的。对上式等号两侧同取自然对数，得

令，ln a =a*，则

变量*和xt已变换成为线性关系。其中ut表示随机误差项。

图9-1　b＞0

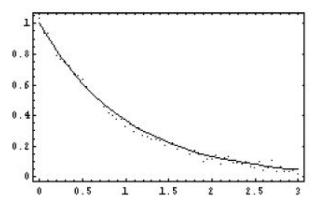
图9-2　b＜0

（2）对数函数模型。

b＞0和b＜0两种情形的图形分别见图9.3和9.4。yt和xt的关系是非线性的。令，则

变量yt和已变换成为线性关系。

图9-3　b＞0

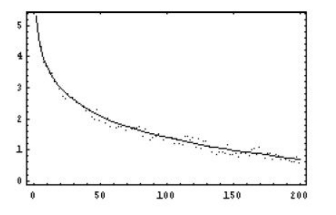
图9-4　b＜0

（3）幂函数模型。

b取不同值的图形见图9.5。yt和xt的关系是非线性的。对上式等号两侧同取对数，得(https://www.xing528.com)

令，则上式表示为

变量和之间已成线性关系。其中ut表示随机误差项。式（9-7）式也称作全对数模型。

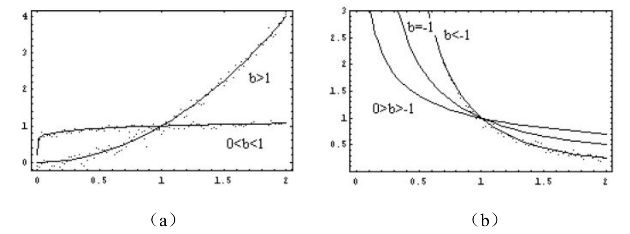
图9-5　b在不同值下的图形

（4）双曲线函数模型。

b＞0和b＜0情形的图形见图9-6和图9-7。yt和xt的关系是非线性的。令，，得

已变换为线性回归模型。其中ut表示随机误差项。

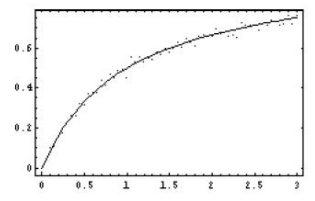
图9-6　b＞0

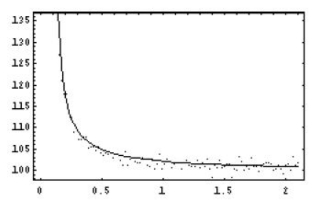
图9-7　b＜0

（5）多项式方程模型。

多项式方程的表达形式是

其中b1＞0，b2＞0，b3＞0和b1＜0，b2＞0，b3＜0情形的图形分别见图9-8和图9-9。令xt1=xt，，上式变为

这是一个三元线性回归模型。

图9.8　b1＞0，b2＞0，b3＞0

图9.9　b1＜0，b2＞0，b3＜0