本节着重介绍ARCH模型的软件操作过程，用White方法检验是否存在异方差的方式较为简单，在回归的基础上，点击Residual Tests/White即可进行White检验（见图18-1）。
图18-1 White检验
如表18-1所示，给出了我国1978—2015年国内生产总值和全国居民消费水平的数据，其中GDP代表国内生产总值，CJ表示居民消费水平。根据下表数据建立含有变量滞后项的回归模型，再对残差序列进行ARCH效应检验。变量的分布滞后模型可以考察变量间的动态关系，同时，为了降低误差，分别对序列对象GDP和CJ取自然对数。故构建如下模型形式：
首先建立含有变量滞后项的回归模型，用普通最小二乘法对上式进行估计，得到残差序列，然后再对残差序列进行ARCH的效应检验。
表18-1 1978—2015年国内生产总值和居民消费水平
注：数据来源于《国家统计年鉴》。
操作步骤如下：
第一步，分布滞后模型的建立。在主菜单中选择Quick/Estimate Equation选项，或者在工作文件窗口的工具栏中选择Object/New Object/Equation选项，弹出方程设定的对话框，如图18-2所示。
图18-2 设定方程
在上述所示的文本框中列出被解释变量和解释变量，在“Method”中选择“LS”估计法，然后点击确定，即可得到如图18-3所示的估计结果。从图中可以看出，在5%的显著性水平下β1、β2通过了t检验，但是常数项和β3未通过检验。改模型拟合优度达到0.998，因而模型的拟合效果很好。
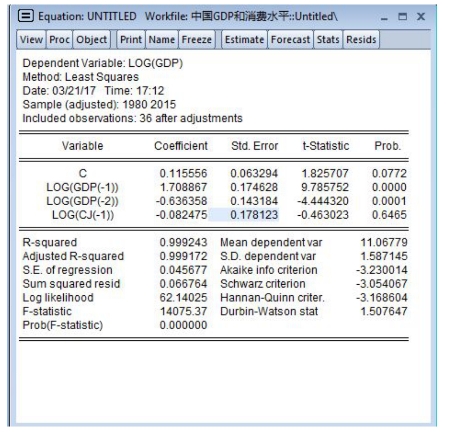
图18-3 分布滞后模型的估计结果
第二步，生成回归模型的残差图。模型完成后，系统会将残差保存到序列对象Resid中。双击工作文件中的Resid序列对象，在打开的窗口中，选择View/Graph/Line选项，得到回归方程的残差图，如图18-4所示。
图18-4 回归模型的残差图
由上图可以看出，残差序列在1995—1998年波动较小，在1992—1995年波动较大，说明有可能存在条件异方差，因而需要对残差进行ARCH检验。
第三步，残差序列的ARCH效应检验。在图18-4页面，在工具栏中选择View/Residual Diagnostics/Serial Correlation LM Test选项，在弹出的对话框中输入滞后期，如输入2，便得到了在滞后期P=2时的ARCH LM检验结果，如图18-5所示。
图18-5 条件异方差的ARCH LM检验结果
如图18-5所示，ARCH LM检验结果的P值大于0.05，不能拒绝原假设，因而可以断定残差序列中不存在ARCH效应。
然后，对模型进行条件异方差的相关图检验，选择工具View/Residual Diagnostics/Correlogram-Q-statistics选项，在弹出的对话框中输入最大滞后阶数，如输入8，得到残差平方的自相关（AC）和偏自相关（PAC）系数，如图18-6所示。
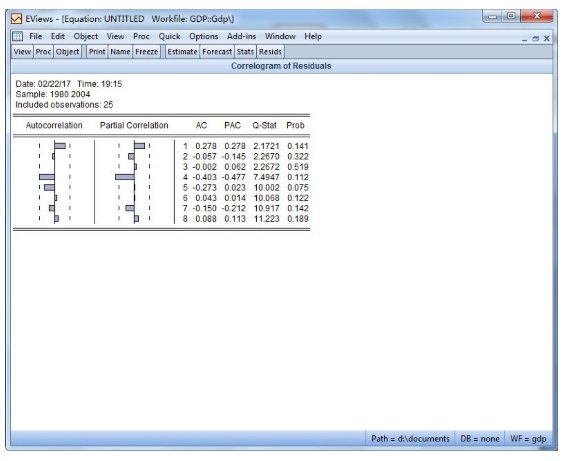
图18-6 条件异方差的相关图检验结果
如上图所示，自相关（AC）和偏自相关（PAC）系数显著为0，由最后一列的P值也可以看出P大于0.05，因而在5%的显著性水平下可接受原假设，即残差序列不存在ARCH效应。
【案例】
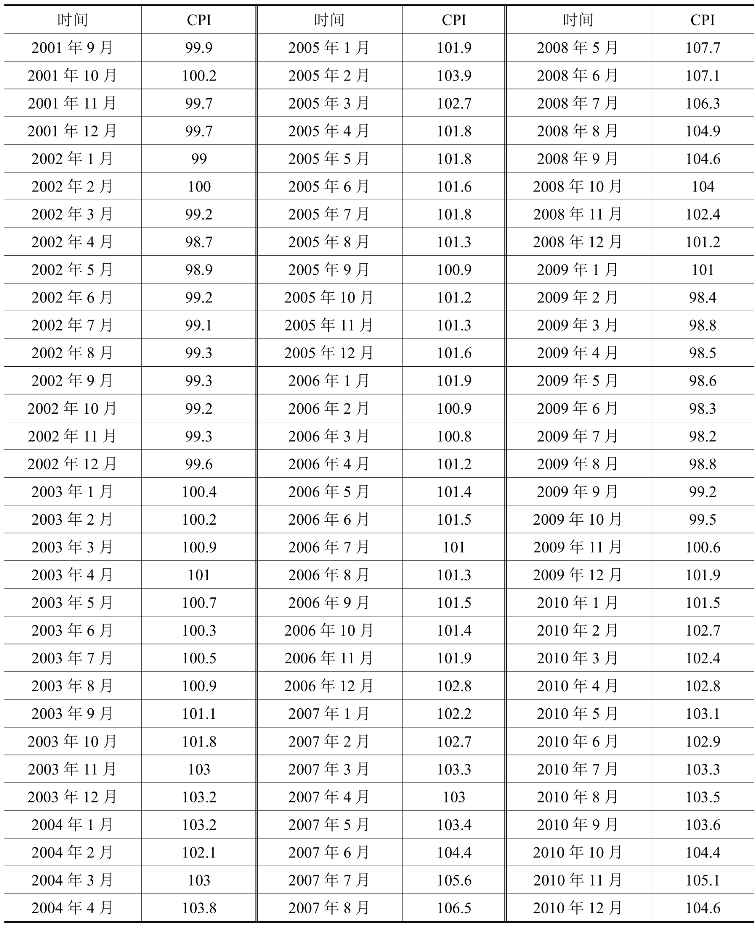
本案例选择2001年1月—2010年12月的CPI数据进行分析，在EViews窗口主菜单栏下的命令窗口中键入如下命令：genr rx=log（x/x（-1）），回车后即形成CPI增长率的数据序列rx。具体数据如表18-2所列。
表18-2 CPI月度数据表(www.xing528.com)
续表
双击选取“rx”数据序列，在新出现的窗口中点击“View”－“Descriptive Statistics”－“Histogram and Stats”，则可得CPI增长率rx的描述性统计量，如图18-7所示：
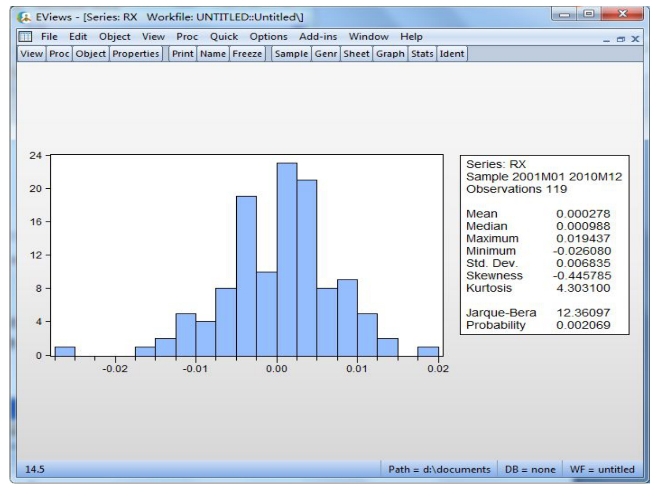
图18-7 CPI增长率的描述性统计量
观察这些数据，我们可以发现：样本期内CPI增长率均值为0.027%，标准差为0.68%，偏度为-0.445，左偏峰度为4.303，远高于正态分布的峰度值3，说明CPI增长率具有尖峰和厚尾特征。JB正态性检验也证实了这点，统计量为12.36，说明在极小水平下，CPI增长率显著异于正态分布。
（1）平稳性检验。
再次双击选取rx序列，点击“View”－“Unit Root Test”，出现如图18-8所示窗口：
图18-8 单位根检验
对该序列进行ADF单位根检验，选择滞后4阶，带截距项而无趋势项，所以采用窗口的默认选项，得到如图18-9所示结果：
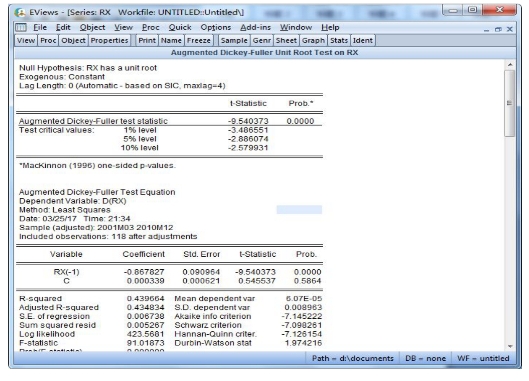
图18-9 rx ADF检验结果
在1%的显著水平下，CPI增长率拒绝随机游走的假设，说明是平稳的时间序列数据。即CPI一般是非平稳的，经常有一个单位根（随机游走），而CPI增长率序列通常是平稳的。
（2）对CPI增长率做自回归。
在EViws主菜单中选择“Quick”－“Estimation Equation”，出现如图18-10所示窗口：
图18-10 对增长率rx做自回归
在“Method”中选择LS（即普通最小二乘法），然后在“Estimation settings”上方空白处输入如图18－10所示变量，单击“OK”，则出现图18-11所示结果：
图18-11 增长率rx回归结果
用Ljung-Box Q统计量对均值方程拟和后的残差及残差平方做自相关检验：
点击“View”-“Residual Test”-“Correlogram-Q-statistics”，选择10阶滞后，则可得CPI增长率残差项的自相关系数acf值和pacf值，如图18-12所示：
图18-12 CPI增长率rx残差项的自相关系数acf值和pacf值
（3）对残差平方做线性图。
对rx进行回归后在命令栏输入命令：genr res1=resid^2，得到rx残差平方序列res1，用同样的方法得到rz残差平方序列res2。双击选取序列res1，在新出现的窗口中选择“View”－“Line Graph”，得到res1的线性图如图18-13所示。
可见
的波动具有明显的时间可变性（time varying）和集簇性（clustering），适合用GARCH类模型来建模。
图18-13 rx残差平方线状图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
