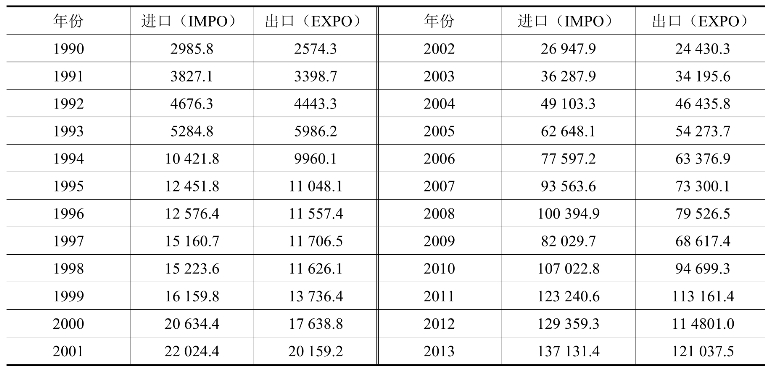
以1990—2013年对数的中国货物进、出口(Lnit,Lnet)货物总额序列为例(数据见表17-1)介绍VAR模型分析。
表17-1 中国货物进出口总额数据 单位:亿元人民币
(1)VAR模型估计。
Lnit、Lnet的时间序列见图17-1。两个序列都是带有趋势的非平稳序列,明显存在某种均衡关系,建立VAR模型的步骤如下。
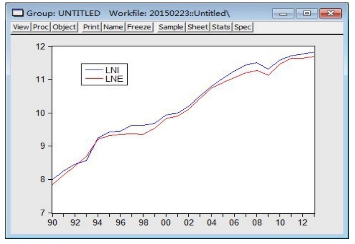
图17-1 时间序列
点击Quick键,选择Estimate VAR…功能,随即打开一个对话框,其中需要做5项选择:①VAR Type(Var类型)选择区含两种选择:无约束VAR(Unrestricted VAR)和向量误差修正模型(Vector Error Correlation)。默认选择是无约束VAR模型。②Estimation Sample(样本范围)选择框要求给出用于运算的样本范围。③Endogenous Variables(内生变量)选择区要求给出VAR模型中所包含的内生变量。④Lag intervals for Endogenous(内生变量滞后期)选择区要求给出VAR模型的滞后期。⑤Exogenous Variables(外生变量)选择区要求给出外生变量(VAR模型中的截距项也属于外生变量)。本例的选择见图17-2。
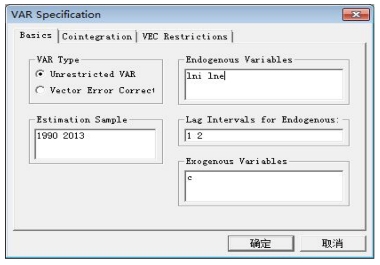
图17-2 VAR模型
点击“确定”键,得检验结果如图17-3所示(截成两部分并列摆放)。第1部分中的两列代表两个方程式,LNI和LNE分别表示两个方程式等号左侧的被解释变量。不带括号的数字表示相应方程式右侧变量的回归系数估计值。回归系数估计值下面第一个带括号的数字表示相应回归系数估计量的标准差。回归系数估计值下面第二个带括号的数字表示相应回归系数估计量的t统计量的值。第2部分给出的是VAR模型中每个方程的10种评价统计量的值。第3部分给出的是VAR模型作为整体的4个评价统计量的值。
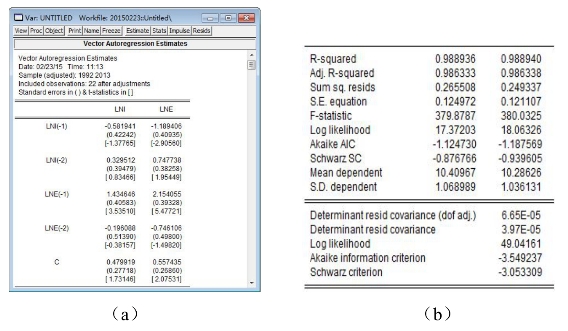
图17-3 检验结果
点击View键,选择Representations功能,得VAR模型的代数式表达如图17-4。

图17-4 VAR模型的代数式表达
(2)VAR模型平稳性检验。
在VAR模型估计结果窗口点击View键选Lag Structure/AR Roots Table功能,即可得到VAR模型的全部特征根(见图17-5)。若选Lag Structure/AR Roots Graph功能,即可得到单位圆曲线以及VAR模型全部特征根的位置图(图17-6)。
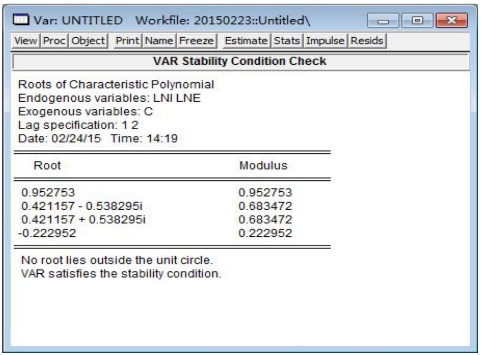
图17-5 VAR模型的全部特征根
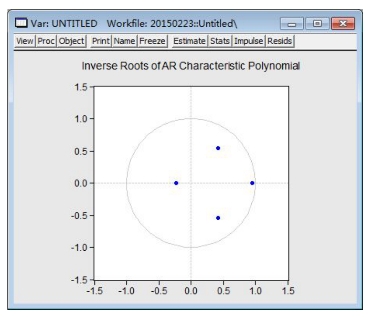
图17-6 单位圆曲线以及VAR模型全部特征根的位置图
(3)协整性检验。
下面介绍协整检验步骤。打开检验协整关系所用变量lnit和lnet的数据组窗口,点击View键,选择Cointegration Test…功能,随即打开一个Johansen Cointegration Test(Johansen协积检验)对话框,如图17-7,其中需要做3种选择:①在Deterministic trend assumption of test(检验的确定性趋势假设)选择框有5种选择。对于lnit和lnet序列选第3种形式,即“数据中有确定性趋势,协积方框中有截距项”是合理的。②Exog variable(外生变量)选择框保持空白。③Lag intervals(滞后期间)选择框选1期(指内生变量差分项个数)。点击OK键,得协整检验结果如图17-8。
输出结果主要分为3部分。第1部分为Johanson协整检验结果,其中包括迹(Trace)统计量检验和最大特征值(Max-Eigen)统计量检验。以检验水平0.05判断,因为迹统计量检验有15.82>15.49,3.0<3.84;最大特征值统计量检验有12.81<14.26,3.0<3.84。
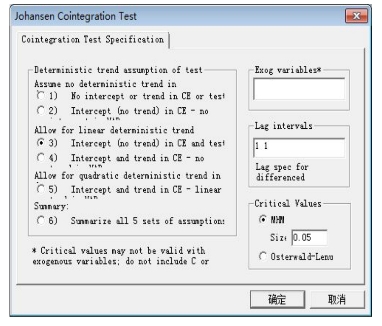
图17-7 Johansen Cointegration Test(Johansen协积检验)对话框
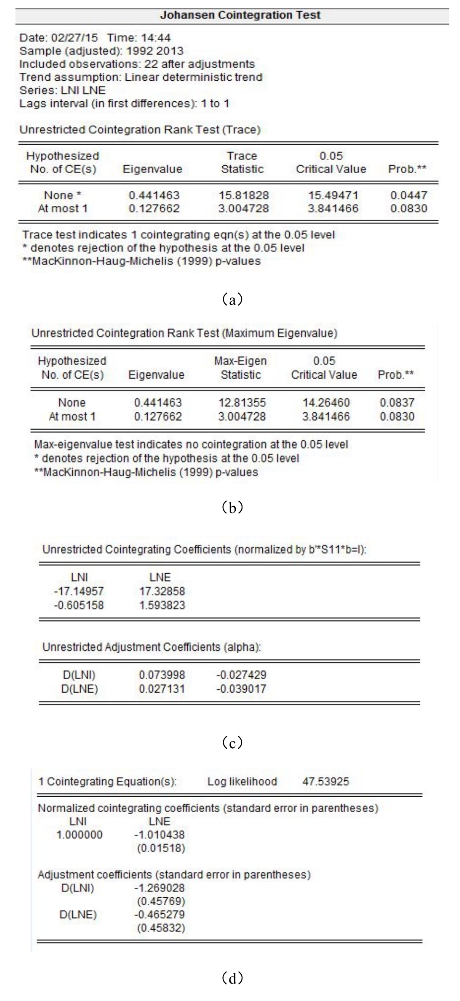
图17-8 协整检验结果
第2部分给出了非标准化的协整参数矩阵, 和调整参数矩阵
和调整参数矩阵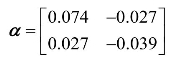 。
。
第3部分给出了标准化的协整参数向量,β=(1 -1.01)′。调整参数向量α=(-1.27-0.47)′。
【案例】
本案例选取2000-2015年我国能源消费(ED)与国内生产总值(GDP)数据进行分析,判断是否能构造VAR模型进行分析,并利用脉冲响应函数和方差分析的方法对模型进行解释和分析,具体数据如表17-2所示。
表17-2 相关数据表
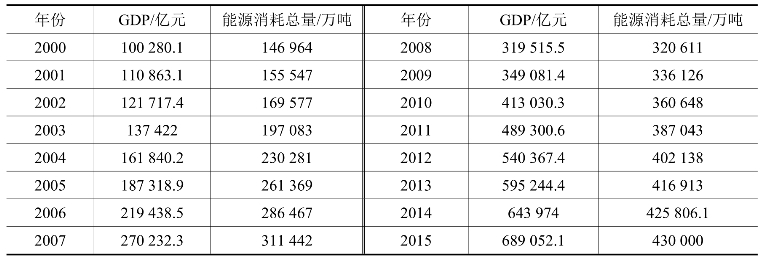
数据来源:统计年鉴。
在进行分析之前,首先需要判断所选的GDP和ED两个变量是否同阶单位根,进而通过EG检验分析是否存在协整关系,如果存在协整关系,则需要通过格兰杰因果检验是否存在统计意义上的因果关系,进而利用SCI原则进行滞后阶数选择,最后方可进行VAR模型的参数估计,进而分析脉冲响应函数和方差分析,讨论模型意义。
1.单位根检验
对所选的GDP和ED两个变量进行单位根检验以确定分别为几阶单整,操作图如17-9所示,而具体结果如表17-3所示。(https://www.xing528.com)
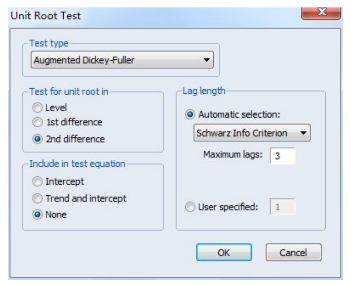
图17-9 单位根操作图
表17-3 单位根检验结果表
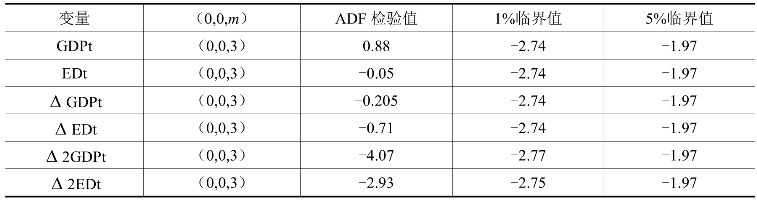
由结果显示,GDP变量的二阶差分,在1%的显著性水平,拒绝存在单位根的原假设,因此变量的序列是二阶单整。同理,对变量ED的序列分别进行同样的操作,结果显示,变量ED二阶差分是平稳的,因此变量ED序列是二阶单整,因此两个变量可能存在协整关系。
2.协整检验:E-G两步法
由平稳性检验发现两个变量均为2阶单整,并且单整阶数相同,可以用E-G两步法检验这两个变量间的协整关系。
第1步:选中变量GDP和ED,点右键选择“Open/as equation”,选择OK后,回归结果如图17-10所示。
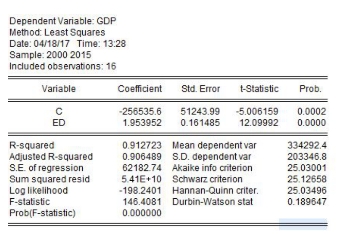
图17-10 回归结果图
选择“Quick/Generate Series”,输入“L1=resid”,将残差序列赋值于L1。
第2步:估计残差的平稳性,点开残差序列L1,点“View/Unit Root Test”,检验对象选择“Level”检查形式选择“none”并根据AIC和SC判断最佳滞后期为1,残差序列L1的平稳性检验结果如下:
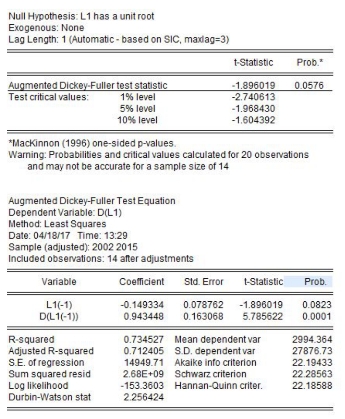
图17-11 残差单位根检验图
结果显示,ADF统计量的值为-2.378,小于5%显著性水平下的临界值-1.968,因此在5%显著性水平下拒绝存在单位根的原假设,即残差序列是平稳的,因此变量间存在长期稳定的均衡关系,是协整的。
3.Granger因果关系检验
选中变量GDP、ED,点右键“open/as Group/view/Granger Causality”,通过检验不同滞后期的Granger因果检验,判断出最佳滞后期为2,检验结果如下:

图17-12 格兰杰因果检验图
结果显示:GDP不是ED的Granger的原因的概率为0.6575,在10%的显著性水平下不能拒绝GDP不是ED的Granger的原因,说明GDP不是ED的Granger的原因。ED不是GDP的Granger原因的概率是0.0941,在10%的显著性水平下拒绝ED不是GDP的Granger原因,表明ED是GDP的Granger原因。
4.VAR模型的估计
GDP表示国内生产总值,ED表示能源消费量,建立VAR模型,选中GDP和ED,点右键Open/as VAR,估计结果如图17-13所示。
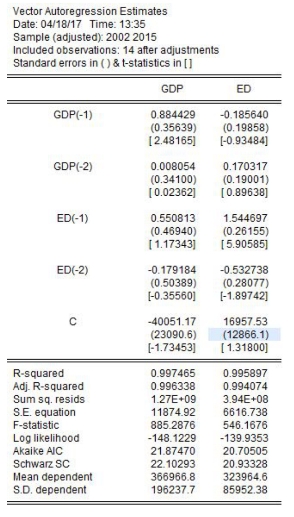
图17-13 VAR模型结果图
从估计结果可以写出VAR模型:
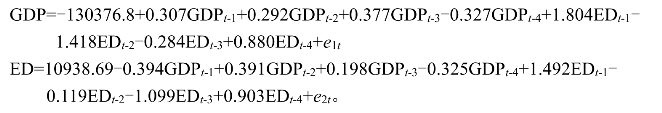
且单位根图形表示结果如图7-14所示。
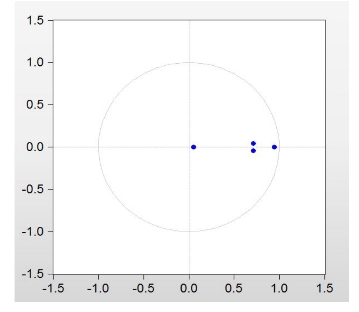
图17-14 单位根的图形表示
5.脉冲响应函数
在上边的VAR模型估计结果的界面下,点击Impulse,选择Multiple graphs和Impulse responses点击OK输出结果如图17-15所示。
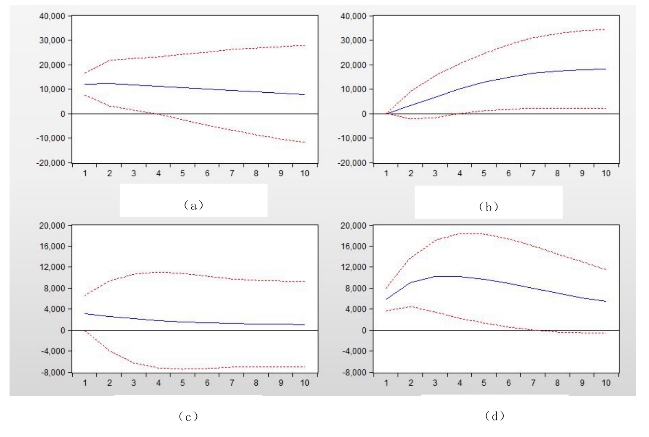
图17-15 脉冲响应函数图
图中实线表示1单位脉冲冲击的脉冲响应函数的时间路径,两边的虚线表示2个标准差的置信区间。(a)表示GDP对自身的响应函数的时间路径,其脉冲响应大约在第2期,约为10 000,以后逐期下降,说明国内生产总值的增长会引起后面各期国内生产总值的增长,且增长的弹性逐渐减小并趋于0。(c)为ED对GDP实施冲击,GDP的响应函数时间路径,响应路径逐渐减小,说明能源消费的增加能引起后面各时期国内生产总值的增长,且增长的弹性越来越小,第6期为0,以后各期为负。(b)是GDP对ED实施冲击,ED的响应函数时间路径,在第一期几乎为0,以后各期逐渐上升,说明国内生产总值的增长会引发后面各期能源消费的增加。(d)为ED对自身的响应函数时间路径,响应路径一直为正,且呈现先上升后稳定的趋势,说明能源的消费会引发后面各期能源消费的增加,且增长的弹性呈现先上升后稳定的规律。
6.方差分解
选择View/Variance Decomposition,点击OK,输出结果如图17-16所示。
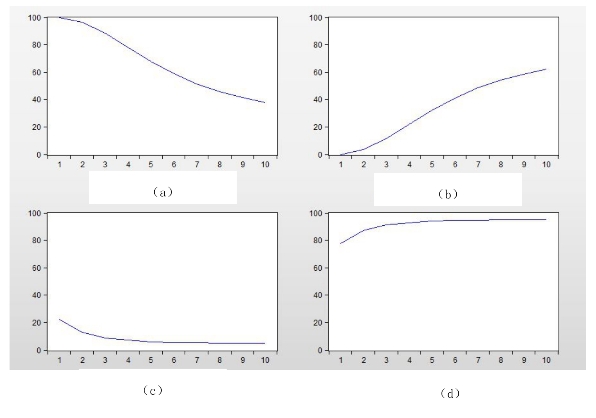
图17-16 方差分析图
图中实线是方差分解的时间路径,(a)是GDP对自身的方差分解的时间路径,时间路径一直为正且不断下降,说明当期国内生产总值对以后各期国内生产总值的贡献越来越小,随后各期间中自身变动的贡献率维持在20%左右。(c)是GDP对ED的方差分解时间路径,时间路径一直为正,且一直上升,GDP对ED的贡献率大致维持在10%。(b)是ED对GDP的方差分解时间路径,时间路径一直为正且不断上升,说明ED对GDP的贡献越来越大。(d)是lnED对自身的方差分解的时间路径,时间路径一直为正且上升后趋于稳定,LnED对自身的贡献率大致维持在80%。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




