假设检验的步骤及方法简析

设某厂批量生产一种直径为100mm的轴，随机抽取一个16根轴的样本，计算出平均直径（样本均值）为110mm，方差为100，要检验的是生产线是否出了问题。换句话说，要检验总体均值是不是100mm。

（1）建立关于总体的原假设和备择假设。

假设检验的第一步是建立要检验的假设。

正式的假设检验涉及在两个相互矛盾的假设之间进行选择，一个是原假设（null hypothesis）；另一个是备择假设（alternative hypothesis）。原假设通常用H0表示，备择假设用Ha或H1表示。下面是关于该轴总体均值的原假设和备择假设：

以上形式给出的这种类型的检验为双侧检验。若备择假设的形式变为μ＞100或μ＜100，则称为单侧检验。

（2）计算检验统计量。

假设检验的逻辑是检验由样本数据提供的结果是否为小概率事件，那么如何对此进行判断呢？在假设检验中，做法是构造一个检验统计量，这个检验统计量及其抽样分布是进行假设检验的基础。我们用样本估计值计算出原假设成立的情况下该检验统计量的值，然后根据它的抽样分布（如正态分布、t分布、F分布等）就可以得到该检验统计量的值出现的概率，即用于检验的样本估计值出现的概率，从而根据概率值的大小进行判断。

在轴直径检验的例子中，涉及的是总体均值的检验问题。由前面有关区间估计的介绍可知，从正态总体中抽取一样本，其样本均值将服从均值μ，标准误差为的正态分布，即

式中，μ和σ分别为总体的均值和标准差。如果σ为已知（如σ=8），Z就是一个理想的检验统计量，其抽样分布为标准正态分布，在原假设H0成立的情况下，μ=100，该检验统计量的值可以计算为Z=5。

问题在于，一般情况下总体标准差是未知的，因而只能由样本数据得到它的估计值：(www.xing528.com)

用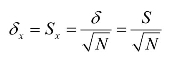作为δx的样本估计值，重新构造检验统计量

注意这个t统计量与Z统计量的区别，它不再服从标准正态分布，可以证明，它服从自由度为N-1的t分布，即

在例子中，样本均值，样本标准差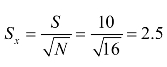，，在原假设成立的情况下，μ=100，因此t=4。

至此，轴直径的例子中，构造一个t统计量作为检验总体均值的检验统计量，其抽样分布是自由度为N-1的t分布，这种采用t统计量作为检验统计量的假设检验是计量经济分析最常见的一类检验，叫做t检验。

一般性推广，设样本估计值，样本估计值的标准误差为（其中Se是standard error的英文缩写），则采用的检验统计量为

需要注意的是，只有在样本统计量服从正态分布的情况下，用它构造的t统计量才服从t分布。

（3）检验原假设，得出关于原假设是否合理的结论。

如果计算的t统计量的值出现的概率小于5%，则拒绝原假设，否则接受原假设。（拒绝域与接收域）