中档题：综合运用余角相关知识的难题

中档题的难度介于简单题与难题之间。它的难度主要不是表现在知识点的生僻程度上，而是表现在知识点的综合程度和已知条件的复杂程度上。通常情况下，中档题会同时考查多个知识点，并且提供多个已知条件，并要求学生对这些知识点和已知条件综合运用。看下面这道题：

【例题2】

如图10-1，在Rt△ABC中，∠C=90°。D为边CA延长线上一点，DE∥AB，∠ADE=42°，则∠B的大小为（　）

A．42°　B．45° 　C．48° 　D．58°

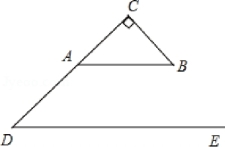
图10-1

【分析】

这是一道偏易的中档题。它涉及的知识点分别是：直角三角形的内角关系和平行线定理。题中给出的条件分别是：“Rt△ABC”，“∠C=90°”，“DE∥AB”，以及“∠ADE=42°”与上一题相比，这道题的难度显然高出一些。学生需要综合利用已知条件和知识点才能把题目顺利做出来。(www.xing528.com)

如果我们的基础知识足够扎实，直接在草纸上做出来也没关系。不过万一你在考场上找不到思路，也没有关系。马上拿出笔，画出一张思维导图，问题自然迎刃而解（当然，前提是你已经掌握了考查的知识点）。

接下来让我们看一下如何用思维导图解题。

【导图解题】

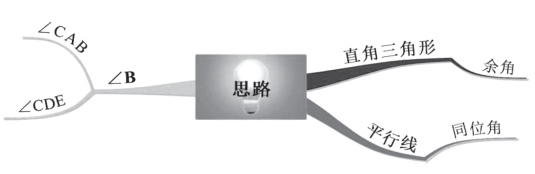
图10-2

首先，我们看一下这道题都涉及哪些知识点。当我们通过常规方式无法找到做题思路的时候，不妨换一个角度去看待试题。出题者之所以会考查一道题，肯定是因为这道题包含了他想要考查的知识点。如果我们能把这道题考查的知识点都列举出来，做题的思路也许就会与我们不期而遇。

就这道题而言，其考查的知识点主要是直角三角形和平行线。与直角三角形有关的知识很多，比如勾股定理，两个余角之和是90°等等。这些知识中与本题直接相关的是余角的相关知识，所以我们把这个知识点写在第一个分支。与平行线有关的知识也有很多，比如同位角和内错角定理，但是本题能用上的知识只有同位角。

接下来，让我们回到问题：想要知道∠B的大小，只要知道∠CAB即可，因为根据余角的知识，这两个角的和是90°。那么，我们怎样才能知道∠CAB的大小呢？根据平行线中同位角的知识，我们知道，∠CAB和∠ADE是相同的，而题中已给条件是“∠ADE=42°”，所以答案不难得出，正确选项是C。